
TsOS_Ekzamen_2021_1
.pdf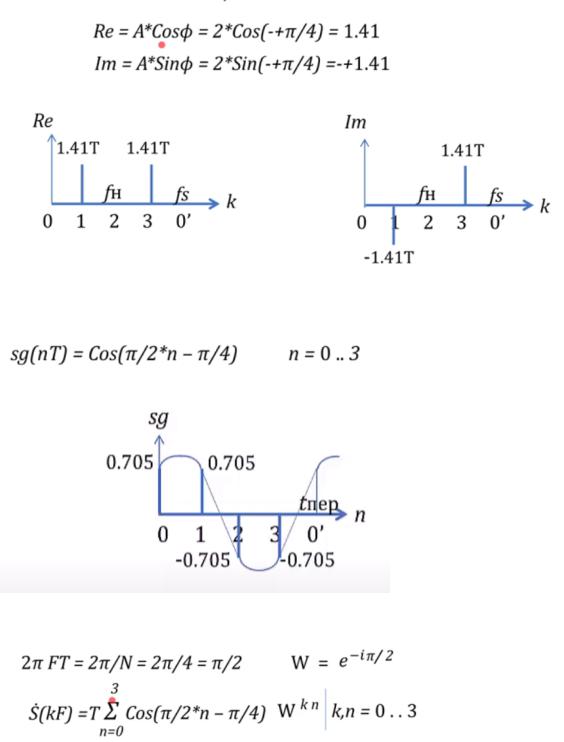
Теперь осталось предсказать Re и Im:
3. Вычислить и изобразить функцию
Подставляем значения n, получаем кривую
4. Вычислить ДПФ заданной ф-ции
Формула ДПФ приобретает такой вид (см. вопрос 11 - вывод формулы ДПФ)
Cos подставили из формулы sg(nT).
ДПФ вычисляем графическим способом. Перебор будет по k, в каждом переборе по k будет перебор по n. Жирные стрелочки равны значениям из предыдущего пункта. На каждом переборе по k делаем поворот жирной стрелочки на угол, соответствующий W, т.к. углы получаются отрицательные,
поворачиваем по часовой стрелке. на каждом переборе, вычисляем сумму(по действительной и мнимой оси)
По получившимся суммам рисуем отдельно реальную и мнимую составляющую
спектра.
Формула ОДПФ
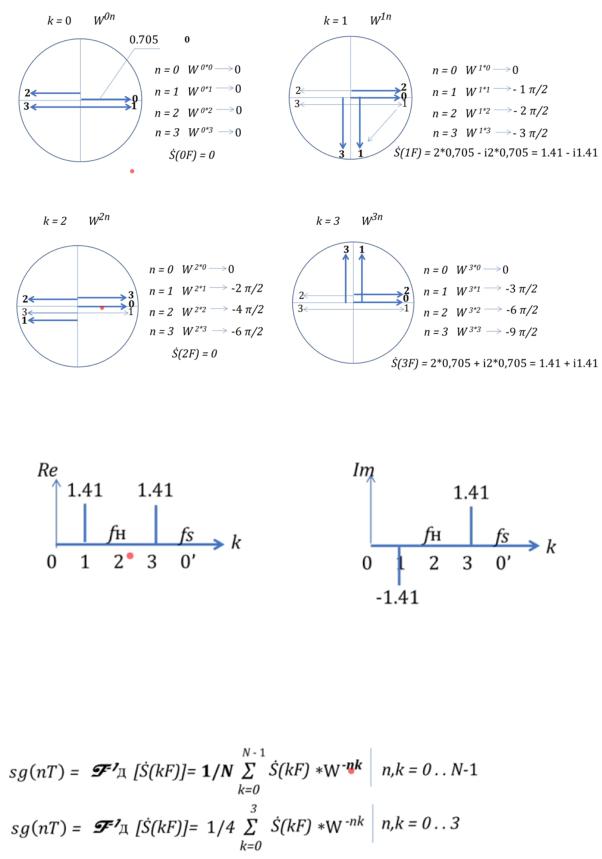
По спектру хотим получить исходный сигнал. Выписываем формулу обратного преобразования Фурье по принципу симметрии. Перебор будет по n, а внутри этого перебора по k.
Нас интересуют только k=1 и k=3, т.к. на 0 и 2 спектр равен 0. По горизонтали реальная часть спектр, по вертикали-мнимая. на каждом этапе делаем поворот треугольника на угол W, вычисляем сумму( в сумме только действительная часть, т.к. мнимые части расположены противоположно и компенсируются).
получаем из сумм исходный сигнал.
ДПФ, ОДПФ комплексных ф-ций.
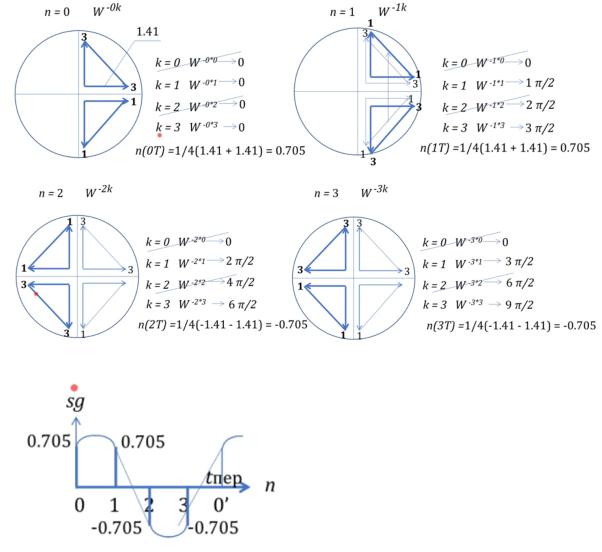
sg(t)- комплексный сигнал (см. ниже)
В природе таких конструкций cos+isin не существует, она создана искусственно, чтобы получить наиболее тонкое представление о фазе сигнала. Фаза содержит больше информации, чем амплитуда. Если речь идет о постоянной частоте, то (t) заменяется на f1t+ 0. Возьмем данные из прошлого примера. Подставляем все числа и получаем действительную и мнимую часть сигнала.
Преимущество комплексной ф-ции: Одна гармоника полностью уложилась в
периоде частоты.
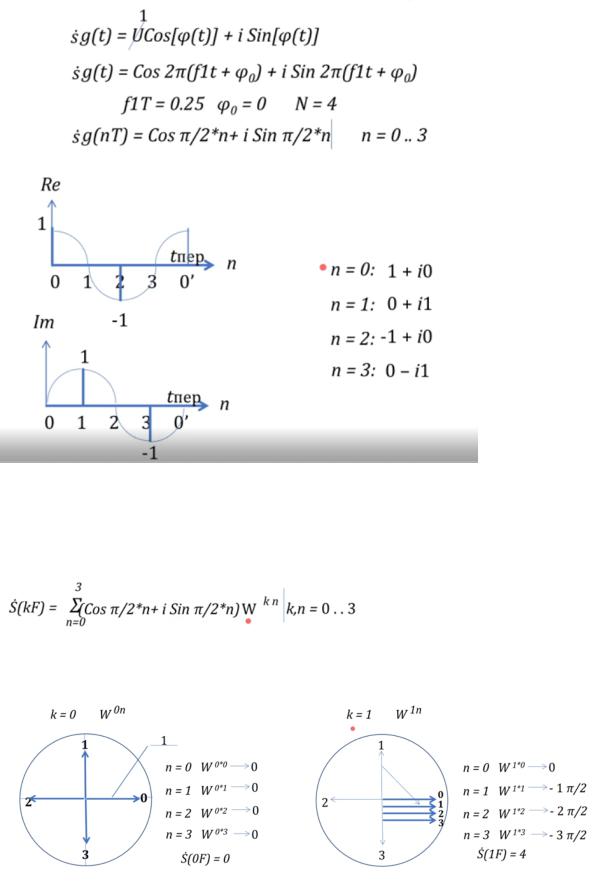
Вычислить ДПФ комплексной функции
Подставляем функцию, полученную ранее
Далее вычисляем спектр графическим способом по уже известному алгоритму (повороты по часовой стрелке).
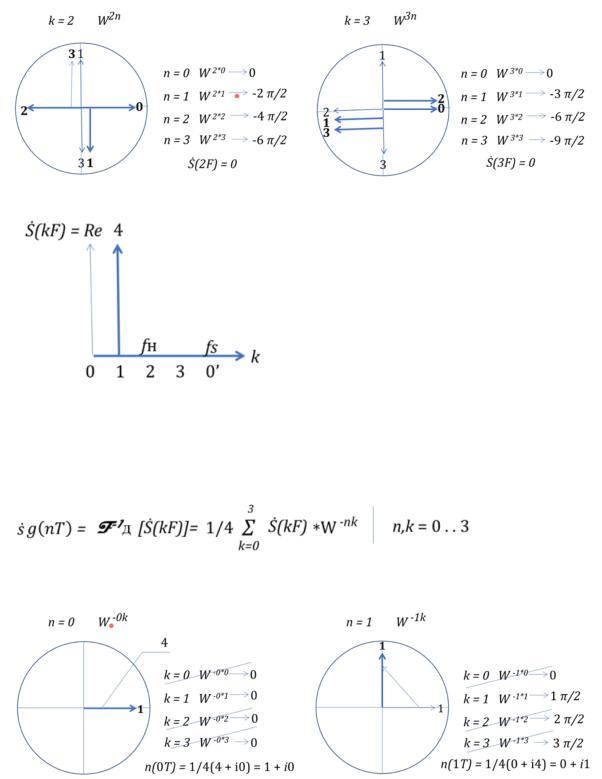
из сумм получили спектр
Зеркалки нет.
Вычислить ОДПФ.
Все то же самое, только вместо сигнала sg(nT) стал спектр S(kF) и nk поменялись местами и стали с минусом.
Поворот против часовой стрелки. k, на которых нет спектра зачеркиваем и все по известному алгоритму.
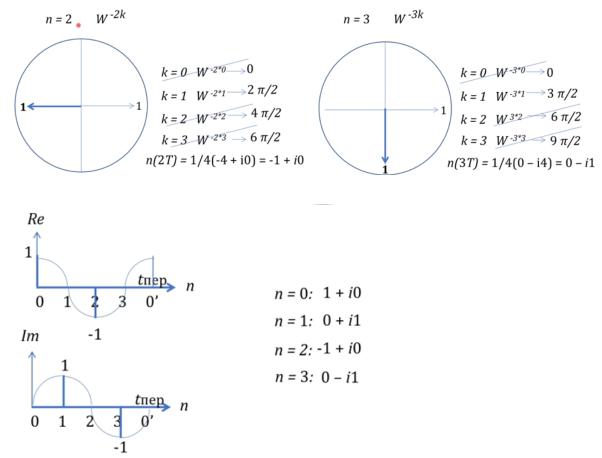
из полученных сумм, получаем Re и Im
13. ДПФ, ОДПФ сигналов.
в работе
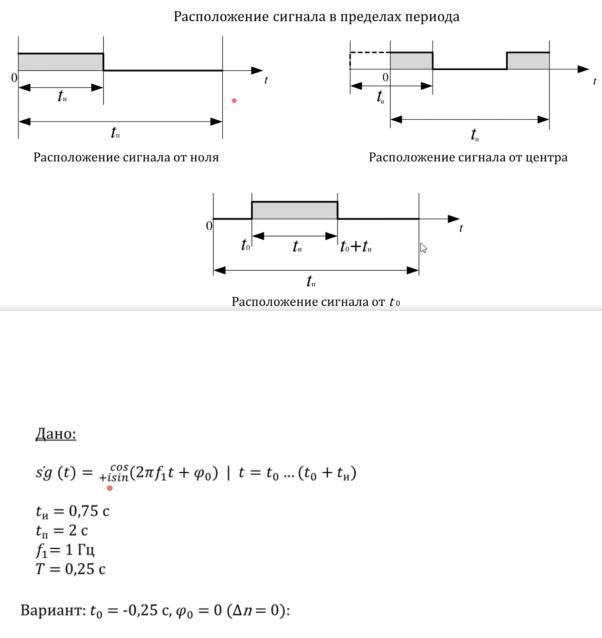
По жизни нужны не периодические функции, а нужны сигналы. Надо удлинить период как можно больше, чтобы сам сигнал занимал только часть, причем желательно как можно меньшую, от периода. (tи-сигнал, tп-период) На практике период по сравнению с сигналом должен быть не так уж сильно удлинен. Достаточно удлинить опорную функцию вдвое.
А где в пределах этого периода размещать сигнал? По жизни располагают от 0. Но возможны и другие варианты расположения.
Пример вычисления ДПФ
Комплексный сигнал-вырезка гармонической функции. Дан комплексный сигнал с
параметрами. В данном случае расположение сигнала от t0.
1. Продискретизировать и изобразить сигнал
Вычислим относительную (цифровую) частоту
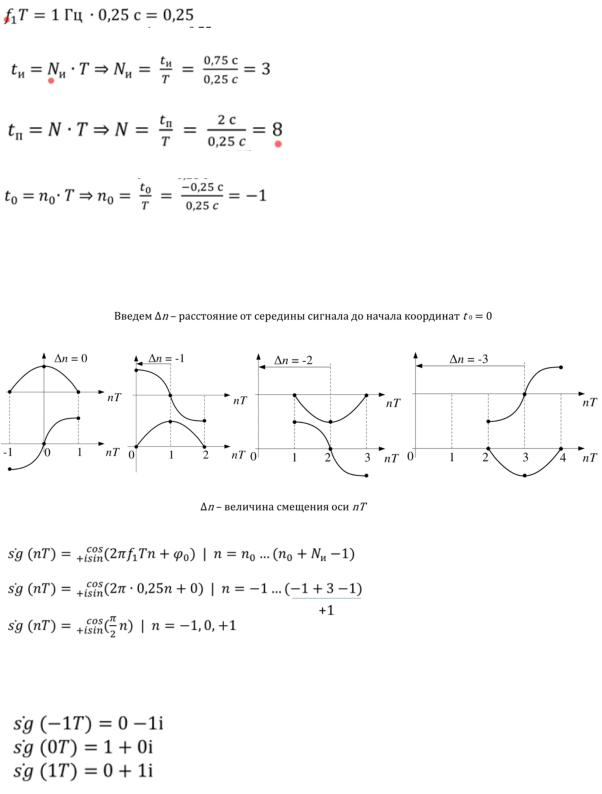
Сколько будет отсчетов Nи
N
n0(откуда будет начинаться)
от -1, симметрично относительно 0 (сверху косинус, снизу синус)
0=0 из дано, фаза измеряется в момент времени, равный нулю, при 0 косинус равен 1, а синус 0, а это значит, что фаза равна 0. Фаза всегда, не смотря, что сигнал смещен, измеряется в 0.
С учетом всех преобразований запишем сигнал
почему Nи-1, потому что если мерить середины дискретов, то как раз будет на 1
меньше.
Получается в итоге 3 отсчета
Получили изображение сигнала
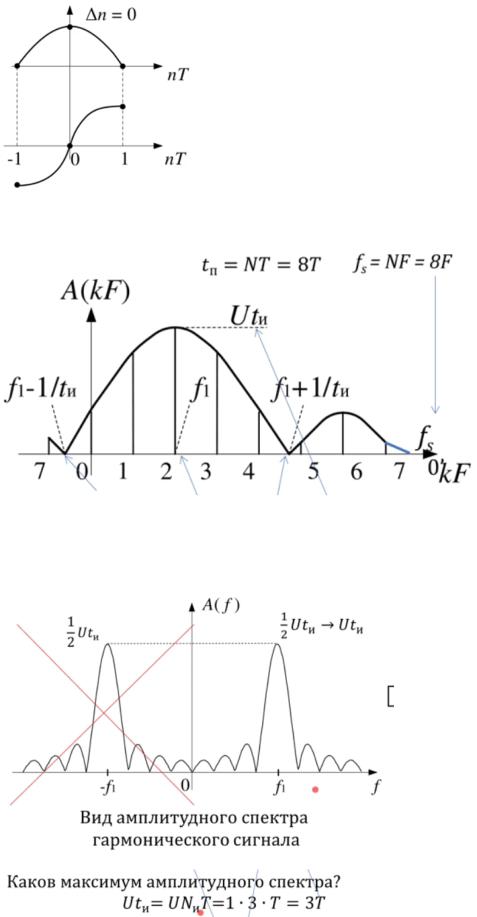
2. Предсказать вид спектра А(kF), Ф(kF), Re(kF), Im(kF).
Как будет выглядеть ДПФ, где будет fs?
Каков будет максимум амплитудного спектра?
Если речь идет о синусоиде, то в гармоническом сигнале есть зеркалка, а у нас комплексный сигнал, у которого будет отсутствовать левая половина, а амплитуда будет не ½, а целая
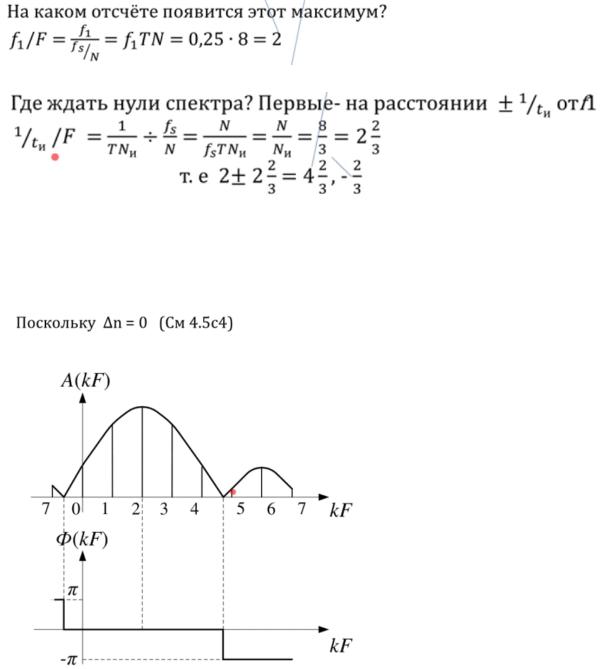
Т.к. у нас будет sinc максимум появится на отсчете, соответствующем f1.
Раз это sinc, то надо ожидать, где амплитудный спектр превратится в 0
т.е. f1+-1/tи. Делим на F, чтобы получить величину в отсчетах.
если прибавить к результату 8 (8-⅔ , 8+4⅔ ), то получим вторые нули после 7 отсчета. Фаза спектра.
В пределах положительного лепестка (тот, который большой) она будет равна 0, а в пределах отрицательного (те, что маленькие) станет - и +
Теперь вычислим Re и Im
в Re маленькие лепестки станут отрицательными, Im будет 0.
