TsOS_Ekzamen_2021_1

Условно забываем сопротивление R из ( ) = 2/ → ( ) = 2 и ( ) = ( ).

5. Отношение сигнал / шум

Коэффициент по уровню сигнал/шум равен:

Коэффициент по мощности сигнал/шум равен:

Условно забываем сопротивление R из ( ) = 2/ → ( ) = 2 и ( ) = ( ).

Уточнение: здесь ( )2представляет собой не уровень шума (так как это случайная величина), а среднеквадратичную величину.

При выборе на какой коэффициент смотреть, коэффициент по мощности ( ) лучше,

чем коэффициент по уровню ( ).

Энергетические характеристики в децибелах:

1. Коэффициент усиления или коэффициент передачи

Чтобы перевести коэфф. усиления по уровню из относительной величины в децибелы, необходимо “домножить” на 20lg:

Коэффициент по мощности необходимо домножить на 10lg:

2. Отношение сигнал / шум

Аналогично коэффициенту усиления (пункт 1):

3. Уровень и мощность сигнала

Оказывается очень удобно уровень и мощность сигнала измерять в децибелах, для этого к уровню сигнала применяем отношение:

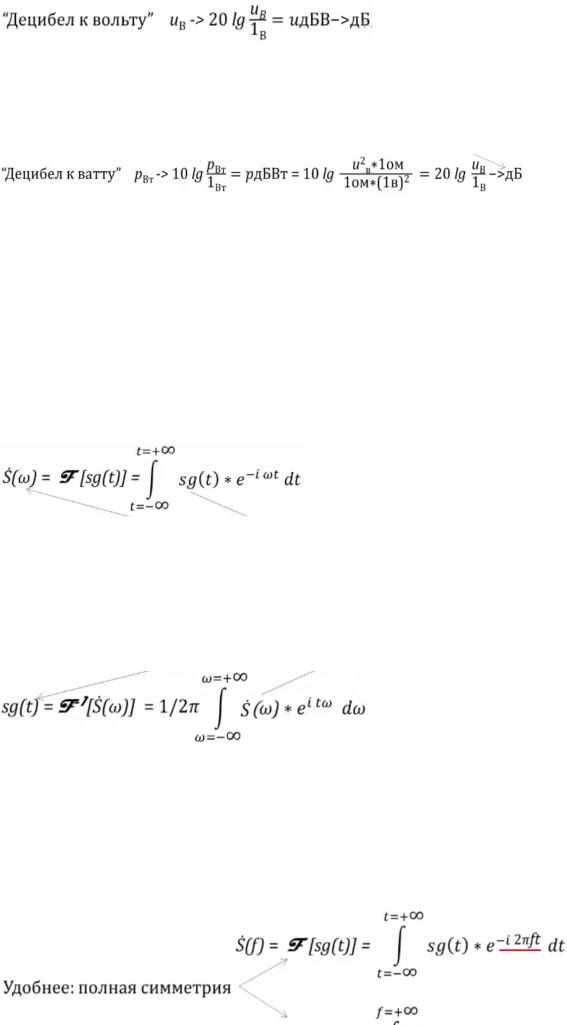
В результате преобразования получаем величину “децибел к вольту” и вольт опускаем и пишем просто “децибел” ¯\_( )_/¯ .

Для мощности сигнала получаем похожее преобразование:

Для перевода мощности в децибелы домножаем на 10lg. = 2/ .

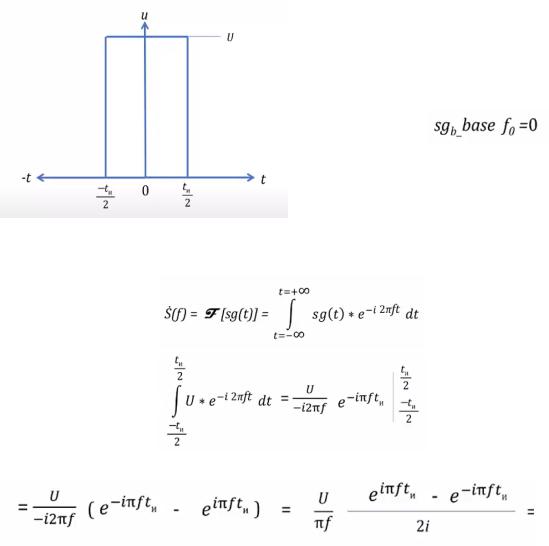
Частотные характеристики сигнала

Эффективным методом анализа и синтеза сигналов является их частотное или спектральное представление.

●Спектр-частотная плотность сигнала есть преобразование Фурье от сигнала, а

преобразование Фурье есть интеграл от − ∞ до + ∞ сигнала * − ω , где ω = 2π - угловая частота сигнала, интегрируем по времени t.

Сигнал - есть временная плотность спектра, если его проинтегрировать по времени,

то получается спектр.

●Существует обратное преобразование Фурье, которое из спектра позволяет получить сигнал, то есть сигнал может быть представлен как обратное преоб. Фурье спектра сигнала (здесь интегрируем по частоте):

Спектр - есть частотная плотность сигнала, то есть то, что можно проинтегрировать по всему диапазону частот, и тогда он превратится в сигнал.

●Если вместо ωвзять 2π (ω = 2π - угловая частота сигнала), то 1/2πиз обратного преобразования Фурье (2-я формула) исчезает, и получаются две симметричные формулы, где - частота сигнала:

8. Преобразование Фурье. Пример 1. Прямоугольные импульсы. Пример 2. Прямоугольные импульсы сдвиг шкалы.

Пример 1. Прямоугольные импульсы.

Есть прямоугольный импульс

длительность и, расположенный

симметрично относительно нуля по шкале времени(базовый сигнал).

Для такого случая в спектре будет содержаться только реальная составляющая, мнимая будет равна

нулю

Общая формула:

Для нашего случая:

Подставляем и переписываем в следующем виде

Далее, пользуясь формулой Эйлера, в которой вместо x используется πи

получаем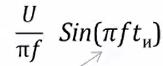

Умножаем и делим на πи, переписываем

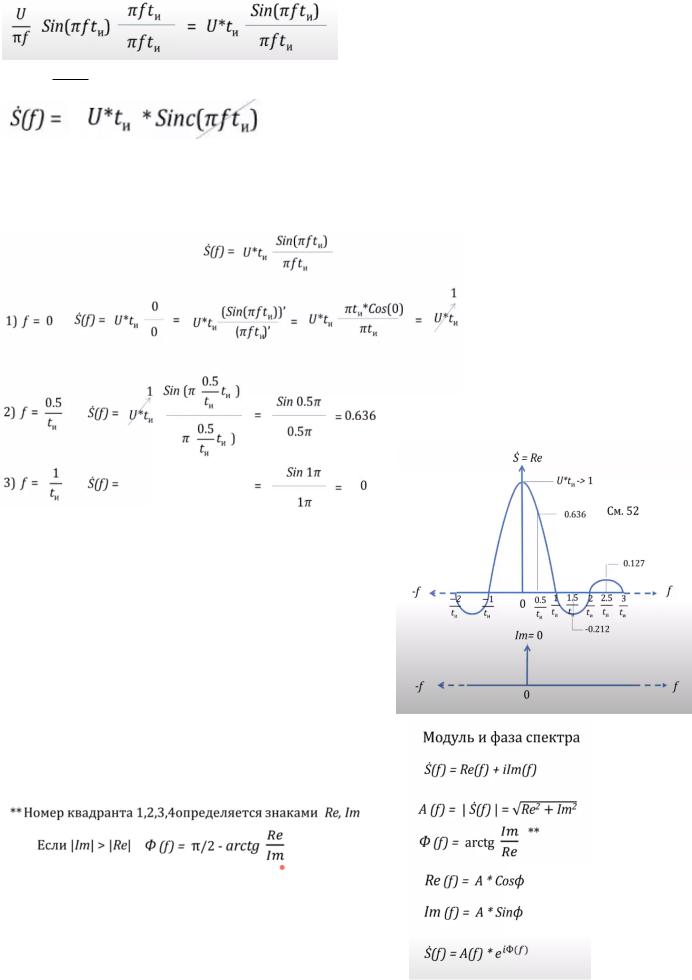
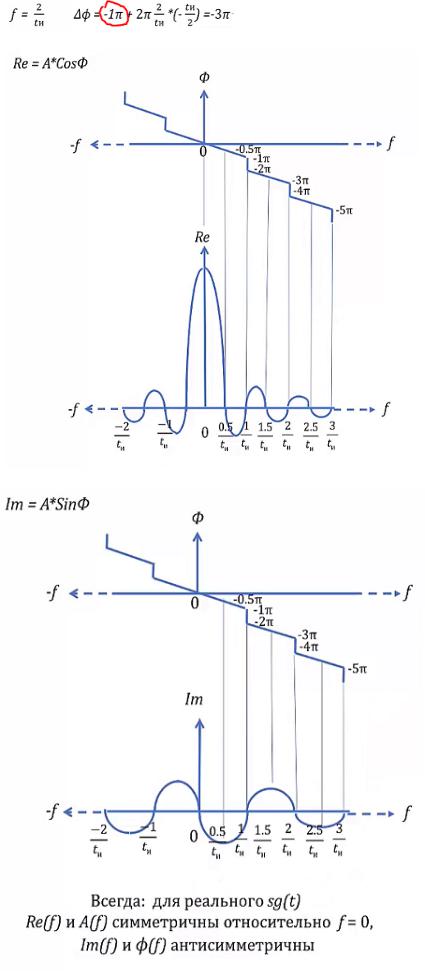
Анализ формулы спектра. Подсчет характерных точек.

Подставляя ноль получаем неопределенность, решаем ее, взяв производные

числителя и знаменателя. Произведение и = 1

Выставляем точки. Получаем кривую sinc. Видим наличие реальной составляющей и отсутствие мнимой.

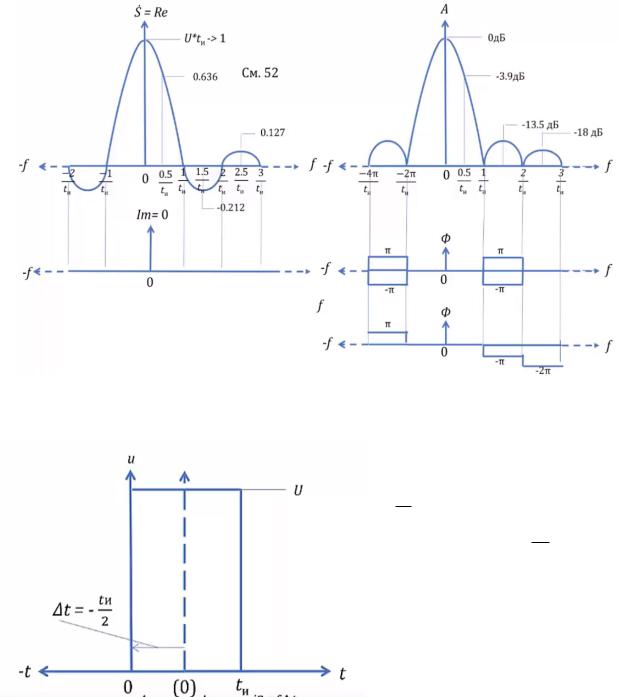
Если есть реальная и мнимая составляющая, можем вычислить амплитуду спектра А и фазу Ф (строки 2,3). И наоборот (строки 4,5).

Также есть второе представление спектра (строка 6)

Амплитуда “перевернет” дуги из отрицательных значений в положительные. Фаза. Каждый раз когда сигнал “проваливается” вниз, фаза меняется от

нулевого значения на π. Поскольку π и− π это одно и тоже, то можно

изобразить так . Для удобства справа от нуля оставим только отрицательные значения, слева - положительные

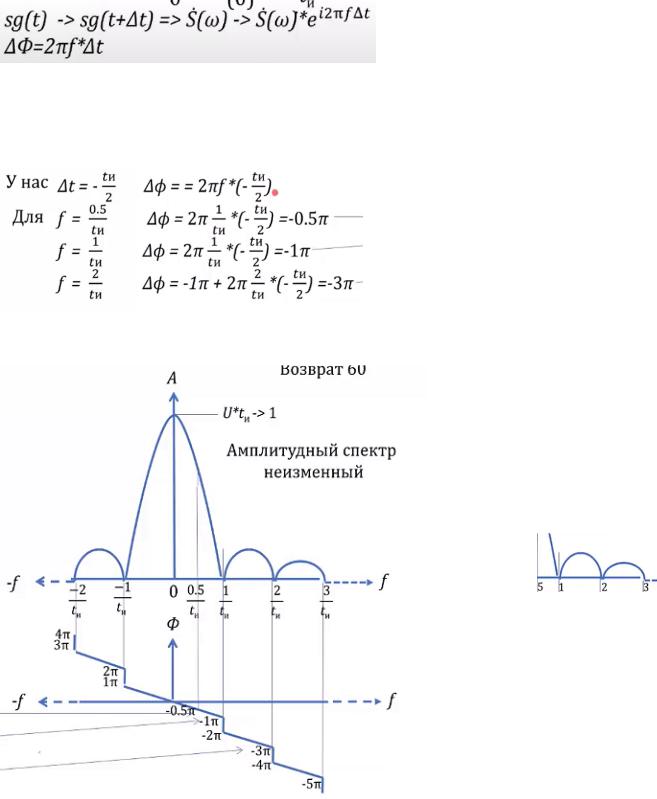
Пример 2. Прямоугольные импульсы сдвиг шкалы.

Раньше импульс был симметричен относительно нуля. Сейчас он сдвинут на

− 2и . Для решения сдвинем

шкалу времени на− 2и . Теперь

импульс симметричен

относительно старого нуля (0).

Прибегнем к следующему свойству преобразования Фурье: если сигнал сдвинут на величину ∆, то спектр этого сигнала окажется домножен на е2π ∆

Так как значение ∆ф = 2π ∆ , то можно сказать, что спектр смещается по

фазе на величину 2π ∆

Считаем характерные точки( изменение фазы для каждого диапазона).

Амплитудная часть спектра не изменяется, только фазовая.

Смещение

линейное, так как

коэффициент f линейно зависим в

формуле

.

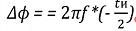В местах “скачков” фаза

дополнительно

изменяется на π.

А в их пределах

продолжает

линейно изменяться. О

них нужно

помнить,

высчитывая следующие характерные точки:

Зная фазу, можно вычислить реальную часть Re. Сравнивая с первым примером. Можно отметить, что получившийся sinc вдвое более “осциллирующий” (рваный). То есть

первый ноль не в 1/ и

, а в 0. 5/ и. И

осцилляция идет с большей частотой.

Считаем мнимую

часть Im, беря за

основу фазу.

получается синусоида с уменьшающейся

амплитудой.

Исходя из графиков,

можем наблюдать,

что Re(f) и A(f)

симметричны, а Im(f)

и ф(f)

антисимметричны.

9. Пример 3. Вырезка гармоники Φ0 = 0. Пример 4. Вырезка гармоники Φ0 = 0. Сдвиг шкалы. Пример 5. Вырезка гармоники Φ0 = π/2. Сдвиг шкалы.

Пример 3. Вырезка гармоники Φ0 = 0.

упр = упрощено.

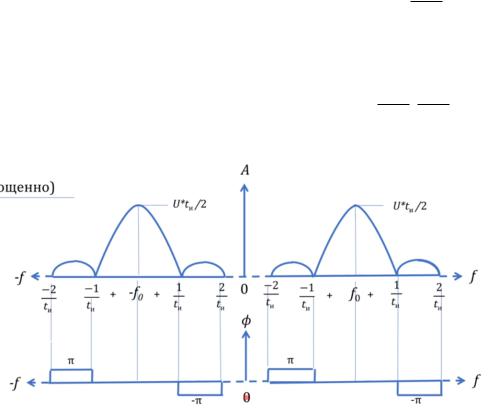
Данный сигнал типа pass, он удобен для того, чтобы его посылать в эфир.

1) Так как это реальный сигнал, то его амплитудный спектр должен быть

симметричным относительно нуля. В то же время это сигнал типа pass, значит его

амплитудный спектр должен сидеть не на нуле, а на его частоте f0 (здесь “спектр сидит” означает, что лепесток с максимальным значением находится в точке f0). А далее всё

исходного сигнала.

2) Так как это реальный сигнал, то его фазовый спектр должен быть

−1 +1

антисимметричным относительно нуля. На интервале ( и ; и ) фаза равна нулю, а

дальше в нулях амплитудного спектра меняет свой знак.

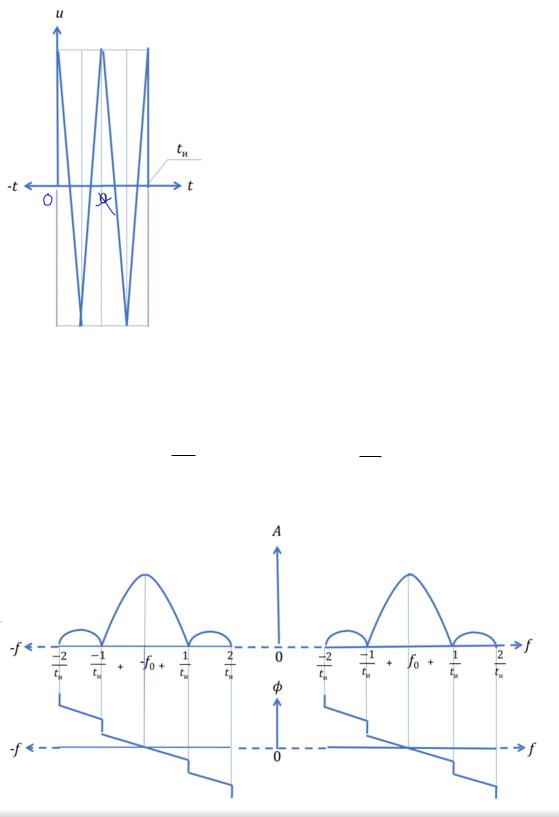
Пример 4. Вырезка гармоники Φ0 = 0.

Здесь сдвигаем не сигнал относительно шкалы времени, а сдвигаем шкалу времени.

Можно взять интеграл для этого случая, но привлекая математику, знаем, что если

шкала времени сдвинута на ∆t, то фазовый спектр умножается на ei2π ∆ . То есть фаза получает линейное приращение ∆Ф = 2π ∆ .

Для нашего случая ∆ = - 2и , тогда ∆Ф = 2π (− 2и ).

Подставляя в это выражение различные значения частоты, получаем приращение фазы в данных точках. Амплитудный спектр при этом не меняется.