
TsOS_Ekzamen_2021_1
.pdf
Слайды без текста:

45. CIC-фильтры. назначение, Интегратор, Гребенчатый фильтр.
CIC - Cascaded Integral Comb (filter) или Каскадный интегрально-гребенчатый фильтр Изобретен в 1979 году Е.В. Хогенауером
Используется как ФНЧ при снятии сигнала с несущей в процессе децимации (Прореживание, каждый d-ый сигнал берется в дело, остальные игнорируются).
Имеет линейную ФЧХ.
Экономичен - не требует умножителей.
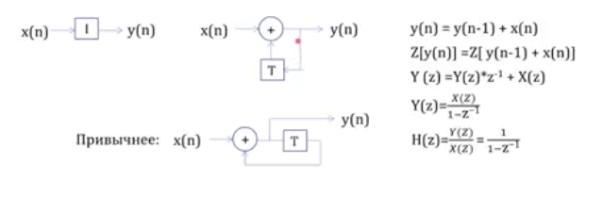
Интегратор:
Привычнее: приходит сигнал, на Т задерживается и суммируется с
вновь пришедшим сигналом.
Вообще, Хогенауер нарисовал немного иначе, будем рисовать точно
так же. Приходит сигнал и суммируется с сигналом, задержанным на
1 такт.
Пометка к формулам сбоку:
1.Записываем со схемы описание с сигналами
2.Возьмём Z преобразование от левой и правой частей
3.Расписываем ( Y(z) - образ Z[y(n)] )
4.Получаем передаточную функцию H(z) (отношение z-образа y
к z-образу x)
Исследование частотного образа интегратора(тут просто формулы раскрывает, можно так и оставить)
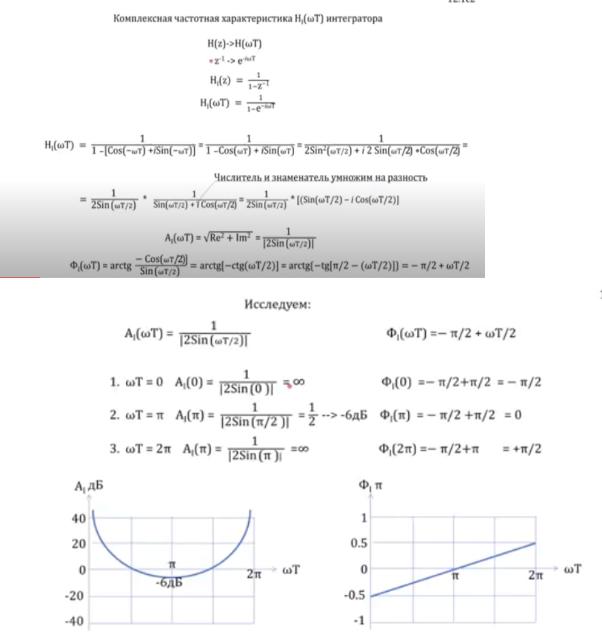
получили АЧХ и ФЧХ интегратора

Гребенчатый фильтр
D - delay - задержка
D - коэффициент децимации
Нижняя схема - привычная. Последовательно включены триггеры, которые задерживают сигнал на несколько тактов.
Верхняя схема: суммируется сигнал и он же, задержанный на D тактов Формулы те же, что и в Интеграторе.
Исследуем АЧХ и ФЧХ, просто идём по формулам.
Исследуем АЧХ и ФЧХ:
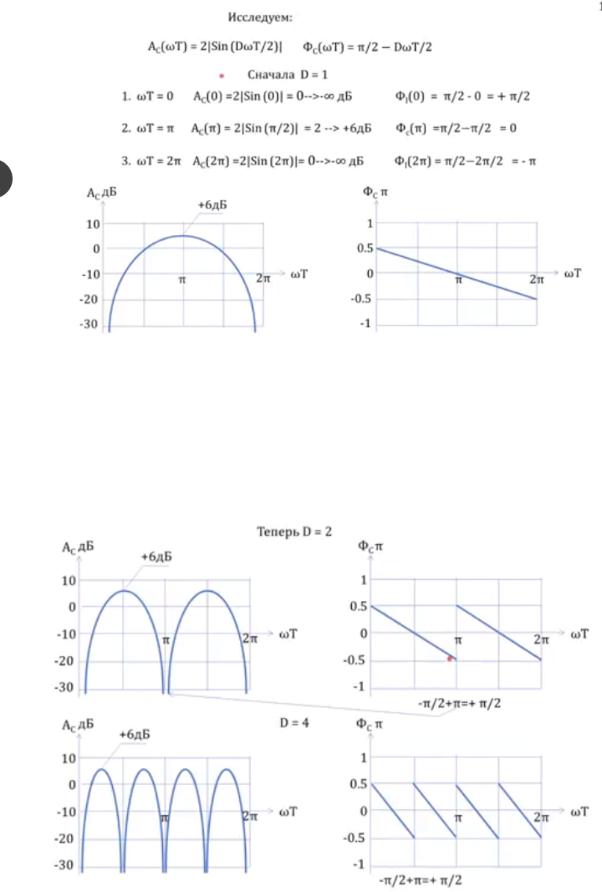
Получили АЧХ и ФЧХ гребенчатого фильтра
Теперь меняем D и смотрим как меняется АЧХ и ФЧХ
при D = 2, фаза вдвое быстрее падает
скачок в pi обусловлен тем, что сигнал меняет знак, поэтому прибавляем pi к -pi\2 и получаем +pi\2
при D = 4 ещё вдвое чаще меняется пила

46. CIC-фильтры. Последовательное включение I и C, CIC-фильтры Nф-го порядка. Децимация. Компенсационный КИХ-фильтр.
Последовательно включим интегратор и гребенчатый фильтр
Частотная характеристика, поскольку последовательно включены две конструкции, есть произведение первой частотной характеристики, на вторую.
Фаза есть сумма первой конструкции со второй.
Исследуем: для D = 1
Комментарии к формулам:
1.Получаем неопределенность 0\0, поэтому схитрим, уберем модуль, поскольку знаем, что оба синуса через 0 проходят. Возьмем производную от числителя и знаменателя
2.Просто раскрываем
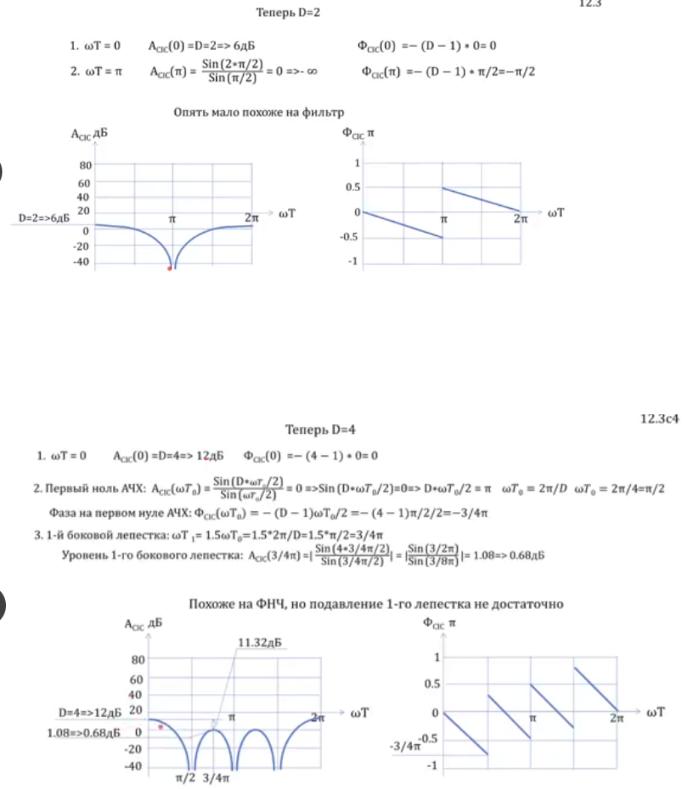
АЧХ и ФЧХ нас не устраивают. Фильтр на всех частотах имеет одинаковое затухание. Фаза равна нулю. Никаких фильтрующих свойств нам не показал.
Возьмём D = 2:
Опять мало похоже на фильтр. С большим натягом можно увидеть очень плохой ФНЧ Поэтому исследуем дальше, возьмём D = 4:
Тут реально можно просто писать по формулам, его комментарии больше для рассуждений, но если
хотите, можете послушать( Лекция 16 2021 год 25 минута)
Но затухание маловато, слишком слабый
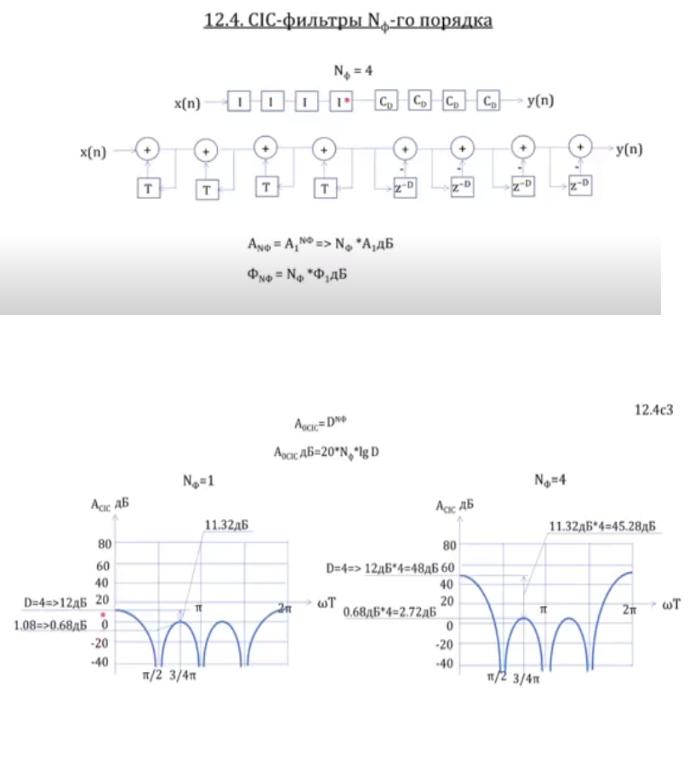
Мы шли по пути увеличения коэффициента децимации, а теперь рассмотрим
CIC-фильтры Nф - го порядка
Т.е. несколько последовательно включенных интеграторов и гребенчатых фильтров Для примера Nф = 4:
D = 4
При последовательном включении A перемножаются, а фаза суммируется
АЧХ получившегося фильтра(справа):
