
TsOS_Ekzamen_2021_1
.pdf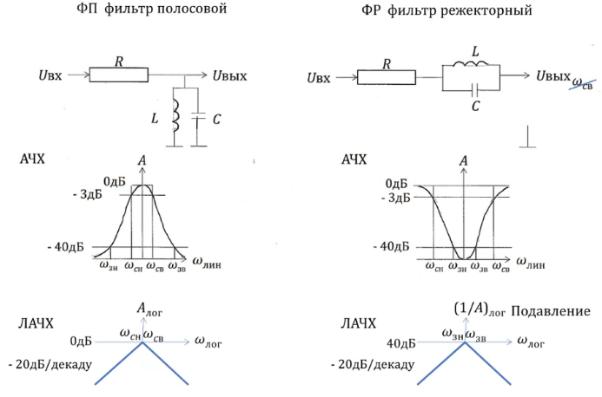
Для ФП и для ФРУ
у ФП конденсатор укорачивает высокие частоты, а катушка низкие. Есть две частоты среза и запирания, нижняя и верхняя.
У ФР, на какой-то полосе частот попадает в резонанс пара LC и не пропускает сигнал слева направо
32. Типы аналоговых фильтров. Фильтр Баттерворта. Определение порядка.
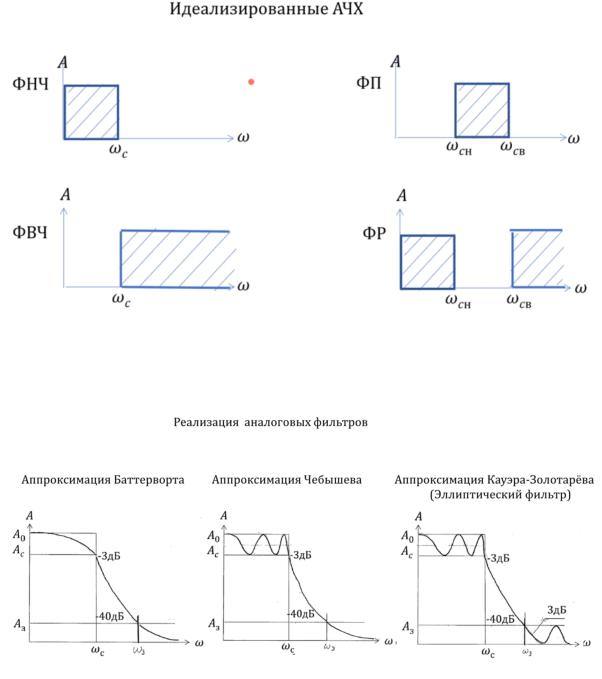
Фильтр низких частот(ФНЧ) пропускает все до ωс. Фильтр высоких частот(ФВЧ) пропускает все после ωс. Полосовой фильтр(ФП) пропускает определенные частоты от ωсндо ωсв. Режекторный фильтр(ФР) пропускает от 0 до ωсн и все после ωсв.
Подбирается некоторая функция, которая позволяет аппроксимировать нужное АЧХ, и зацепившись за эту аппроксимацию, спроектировать аналоговый прототип.
Каждая из аппроксимаций имеет ωс и ωз, полосу пропускания, от 0 до с, т.е. от 0 дБ
до -3 дБ. У всех есть промежуточная полоса и зона полосы запирания.
По рисункам видно, что все аппроксимации ведут себя по разному. Аппроксимация
Баттерворта более плавная в зоне пропускания, также как и в зоне запирания.
У Чебышева зона запирания и промежуточная область совпадает с Баттервортом, а в зоне пропускания, он допускает колебания до -3 дБ.
Эллиптический фильтр, допускает колебания и в полосе пропускания, и в полосе запирания на +3 дБ
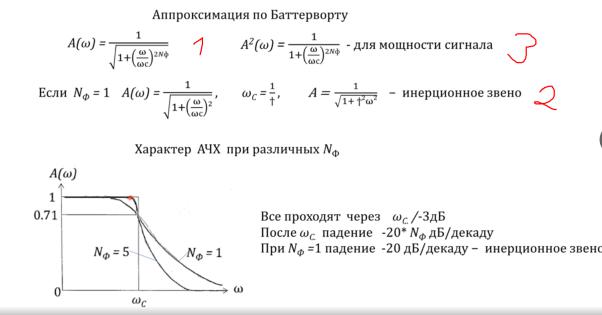
Фильтр Баттерворта.
Аппроксимация Баттерворта имеет формулу помеченную цифрой 1 на рисунке.
Если Ф = 1, тогда смотрим на строку с цифрой 2 на рисунке. Мы знаем, что частота
среза равна 1 делить на t, можем подставить в формулу 1, и получить инерционное звено.
Для будущих расчетов полезно убрать корень, и считать что речь идет не об уровне сигнала, а о мощности. Тогда зависимость будет под цифрой 3, она удобна для
последующих расчетов.

Определение порядка.
Здесь Широ не особо много говорил. Четко шел по формулам и их проговаривал.
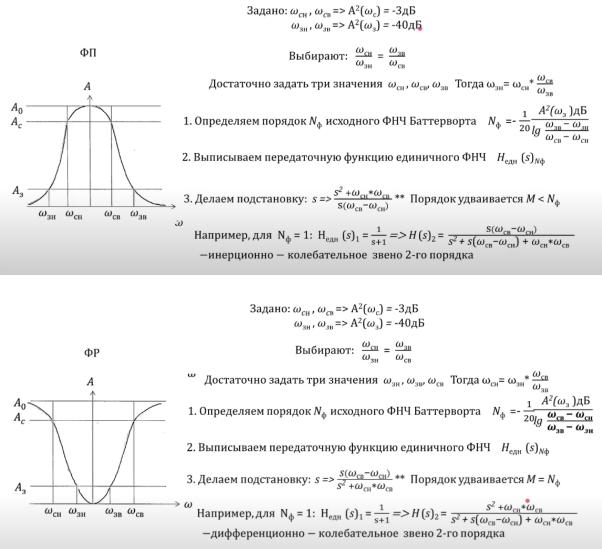
33. Передаточная функция единичного ФНЧ Баттерворта. Передаточная функция аналоговых прототипов ФНЧ, ФВЧ, ФП, ФР.
Передаточная функция единичного ФНЧ Баттерворта.
Единичным фильтром Баттерворта называется фильтр, у которого частота среза равна 1 радиан, тогда его передаточная характеристика вычисляется по формуле:
1
Hедн(s)Nф = Π( − ) , где корни si можно найти, смотря на отрицательную половину
комплексной окружности единичного радиуса.
В зависимости от нужного порядка фильтра выбираем на левой половине нужные
плюса.

Далее не совсем понятно, что требуется от ответа на этот вопрос, т.к. Широ просто прошелся по формулам и в конце сказал, что передаточную характеристику можно рассматривать как у реального аналогового прототипа и делать из него цифровой фильтр.
Передаточная функция аналогового прототипа ФНЧ, ФВЧ, ФП, ФР.
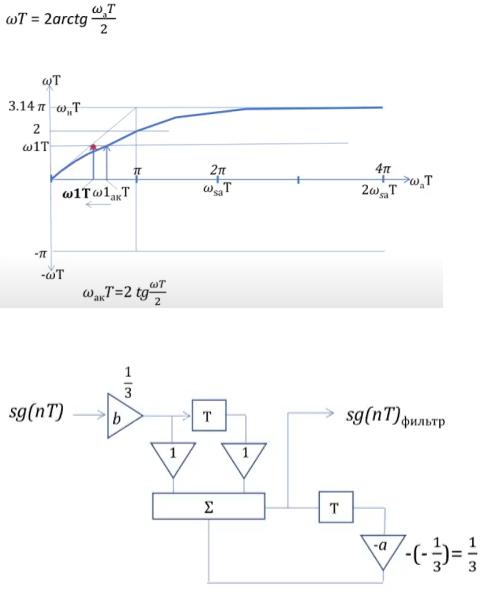
34. Цифровые БИХ-фильтры. Передаточная функция. Функциональная схема фильтров M-Nф порядка
Используя Z-преобразования(билет 35) мы получаем зависимость
Из нее вытекает передаточная функция
Функциональная схема фильтров

35. Билинейное Z-преобразование. Билинейные БИХ-фильтры Nф-го порядка.
Нам надо преобразовать аналоговую частоту H(S) в цифровую H(Z). Делаем подстановку
Но работать с таким выражением очень трудно, поэтому разложим в ряд
И тогда выходит
Выходи очень сильное усечение, за что придется поплатиться искачением цифровой частоты(т.е. будет не линейное). Сделаем замену.
И дальше преобразования
Алгоритм проектирования билинейный БИХ-фильтров
36. АЧХ билинейного ФНЧ 1-го порядка.
Передаточная характеристика H(s) = |
ωаск |
, где |
ωаск |
- скорректированная |
||||||||||||
|
ωаск+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
аналоговая частота среза. Выполним подстановку |
|
= |
2(1− −1) |
. |
|
|||||||||||
|
|
|
|
|
аск |
(1+ |
−1 |
) |
|
|
||||||
После всех преобразований и допущения, что |
|
|
|
|
T = 1 (т.е. сT = 0,927 - в лекции 13 |
|||||||||||
|
|
получим H(z) = |
|
|
|
|
|
|
||||||||
именно такое значение и рассматривалось), |
|
ω |
|
|
|
|
|
ω +1 |
. |
|
||||||
Преобразуем получившееся выражение в комплексную |
|
передаточную характеристику |
||||||||||||||
|
|
3 −1 |
|
|
|
|
||||||||||
(z = eiωT), преобразуем выражение, получим H(i |
ω |
T) = |
( ω + 1) − 2 ω ) |
. |
||||||||||||
|
|
|
|
|
|
|
|
5 − 3 ω |
||||||||
( ω +1)2+4 2ω .
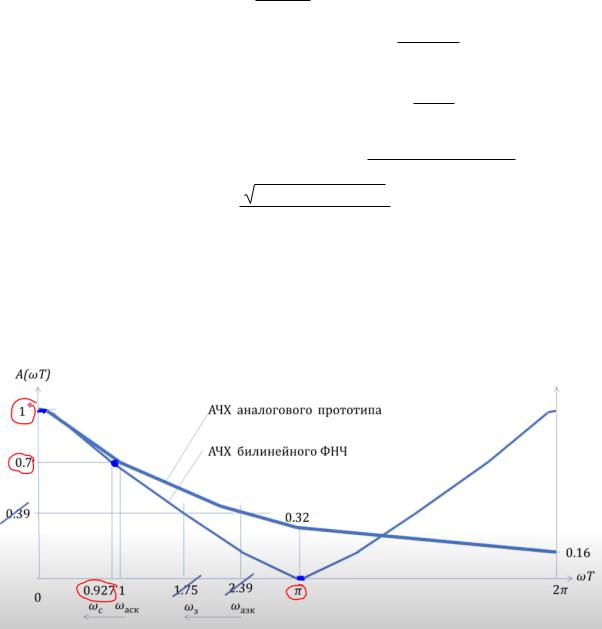
Тогда выражение для АЧХ А(ωТ) = 5−3 ω Исследуем данное выражение:
1)А(0) = 1, А’(0) = 0, т.е. начальные частоты ФНЧ пропускает как нужно;
2)А(0,927) = 0,7;
3)A(π) = 0, А’(π) = 0;
4)ωT > π кривая А(ωT) симметрична относительно ωT = π, т.к. в А(ωT) содержится cos
и sin2.
Здесь смотрим на нижний график, при этом мы его строим по трём точкам (отмечены
синим цветом) со значениями, выделенными красным цветом.
