TsOS_Ekzamen_2021_1
.pdf
29. Расчет КИХ-фильтра Гильберта ФГ
Фильтр Гильберта позволяет имея всего только реальное значение сигнала получить ему мнимого напарника. Из Re -> Im. С тем, чтобы они вместе уже превратились в комплексный сигнал.
Цель, чтобы все частоты сместились на 90 градусов.
Надо чтобы у Re фаза была равна 0, а у Im - π/2
Re(kF) = 0, A(kF) = Im(kF)
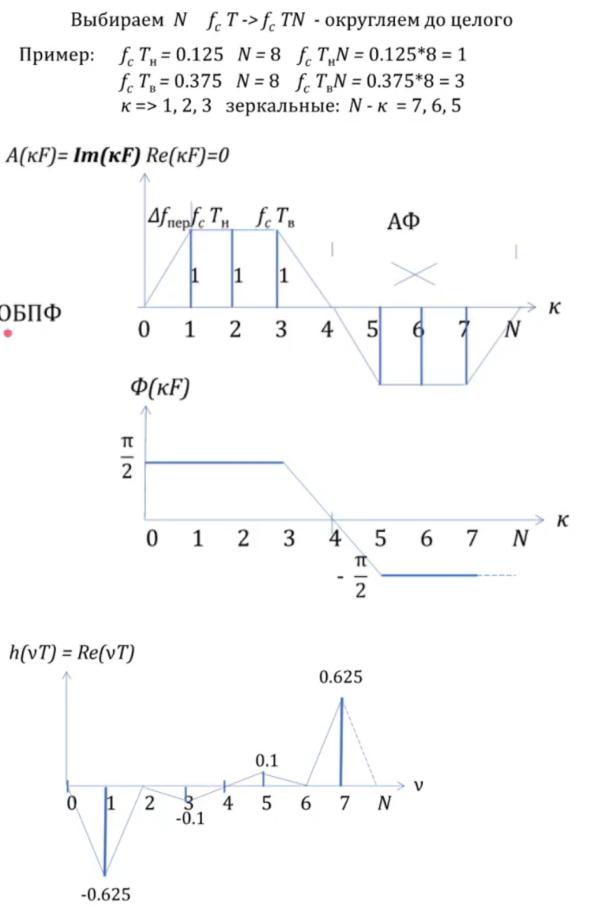
Если подвергнуть ОБПФ:
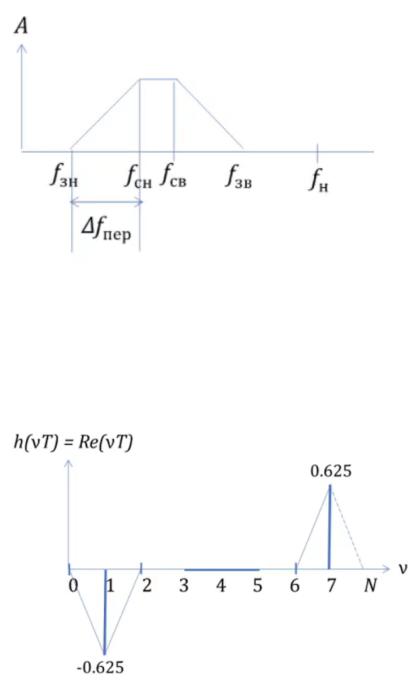
Обнуляем середину. Для этого вычисляем Nф:
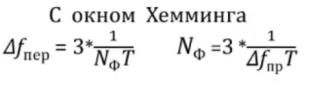Берём ближайшее нечётное!
:
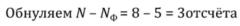Делаем БПФ, получаем колебания Гиббса:
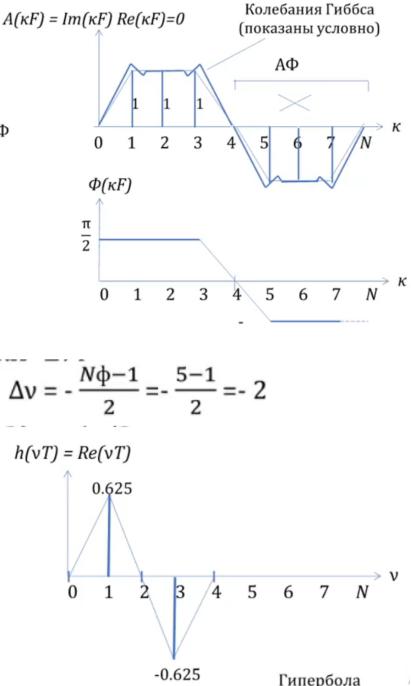
Сдвиг оси времени - смещение по циклу
Меняется только фазовая составляющая:
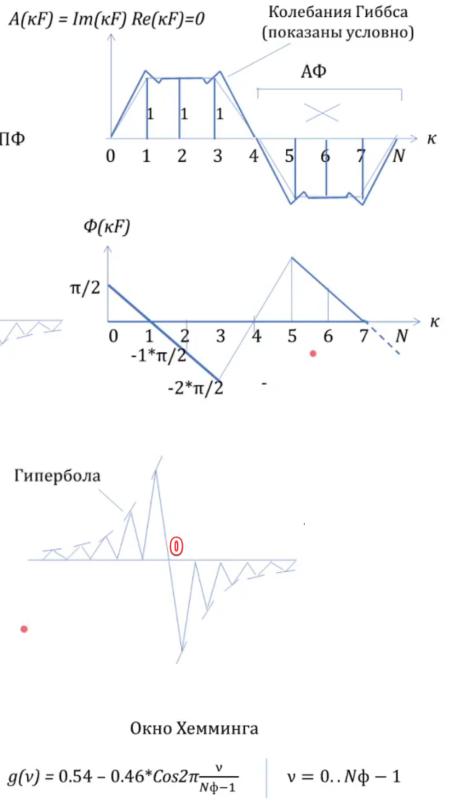
Для больших Nф:
Чтобы избавиться от Колебаний Гиббса, можно воспользоваться окном
Хемминга:
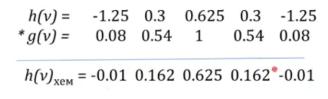ПРИМЕР ИСПОЛЬЗОВАНИЯ
30. БИХ-фильтры. Аналоговые прототипы. Инерционное звено. Частотные характеристики.
Инерционное звено
Звено первого порядка, RC цепочка, хар-ся передаточной функцией H(s)
Умножаем на комплексно сопряженную часть, чтобы убрать мнимую состовляющую из
под знаменателя. Получает АЧХ и ФЧХ известными нам путями
Исследуем АЧХ инерционного звена
Точка перегиба оказывается левее, чем точка омеги среза
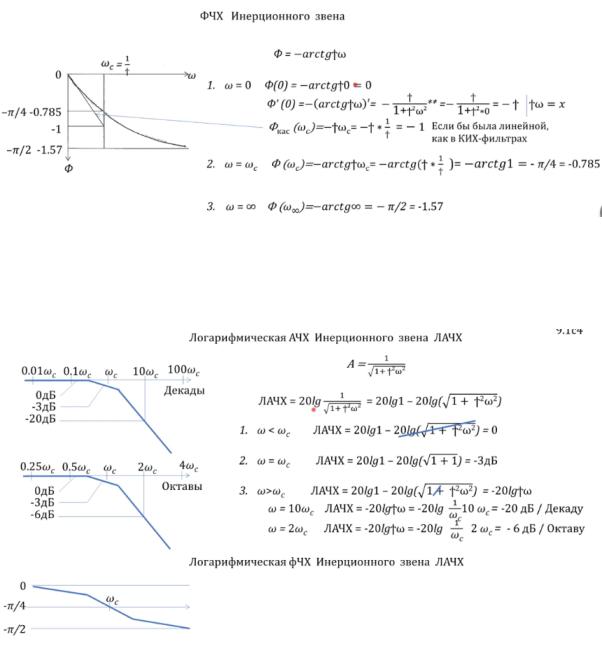
Исследуем ФЧХ инерционного звена
В нуле ноль, с нуля он будет идти по прямой (видно после взятия производной)
Логарифмическая АЧХ и ФЧХ ЛАЧХ при омегеω меньшей омеги среза ωс, будет равно нулю, при равной -3дБ, а при
большем будет увеличивать(уменьшать) -20дБ на Декаду(десятые)
31. Дифференцирующее звено. Частотные характеристики. Звенья 2-ого порядка.
передаточная функция H(s). Подставляем вместо s iw, потом домножаем на комплексно сопряженную часть, дабы избавиться от мнимой состовляющей в
знаменателе.
ищем АЧХ и ФЧХ, они в отличии от инерциального звена уже немного другие.
Исследуем АЧХ Дифференцирующего звена подставляем вместо ωзначения.
В нуле ноль, в беск. стремится к единице. В частоте среза так как ω= 1/T, получим 0.7
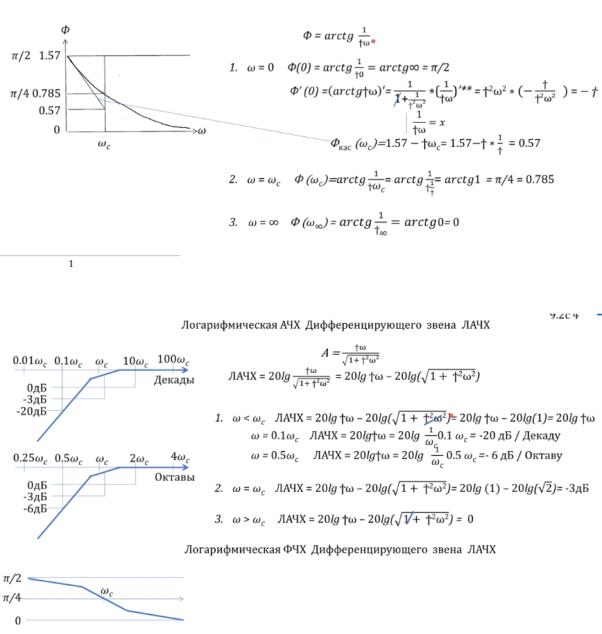
Исследуем ФЧХ
Исследуем ЛАЧХ и ЛФЧХ
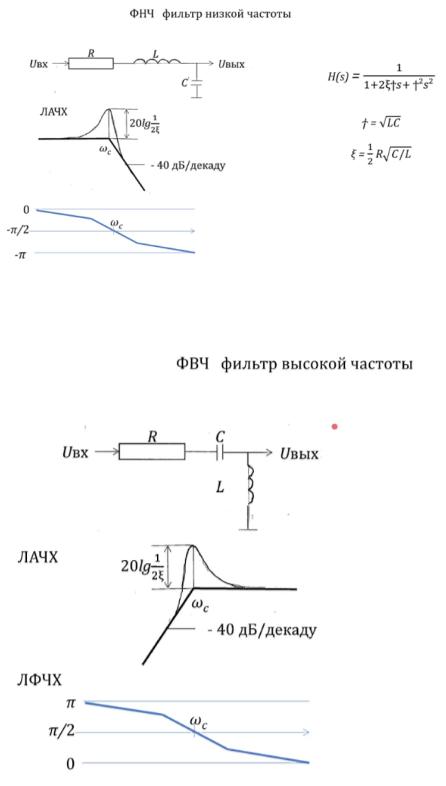
Звенья 2-порядка
Появляется характеристика затухания, и ЛАЧХ дает выброс вверх, и его нужно компенсировать.
Для ФВЧ