
TsOS_Ekzamen_2021_1
.pdf
ЦОС Экзамен 2021
План действий:
Каждый берёт себе по 3 билета. Как только выбрал билет - пиши под ним “В работе”. Если чувствуешь, что не осиливаешь, убери надпись и возьми другой.
Расписываем подробно, иногда катая целые монологи Широ, просто скрины - не канает. Подгоны используем, но лекции в приоритете. Как пример оформления можно использовать первый билет. Каждый вопрос начинаем с новой страницы (Ctrl+Enter).
Срок до 22 июня
Ссылки:
Лекции 2020 Лекции 2021 Билеты 2020 Билеты 2021
Тайминги лекций и билетов 2020 Подгон №1 Подгон №2 Подгон №3 Подгон №4

Предложения/Вопросы:
1. Го каждый вопрос начинать с новой страницы, чтобы если сверху кто-то что-то исправит, форматирование нижних ответов не съехало. Согласен, делаем так!
1. Ключевые слова в наименовании курса. Применение ЦОС в системах связи. Системы связи с кодовым разделением. Шумоподобные сигналы. Коды Баркера.
Ключевые слова в наименовании курса
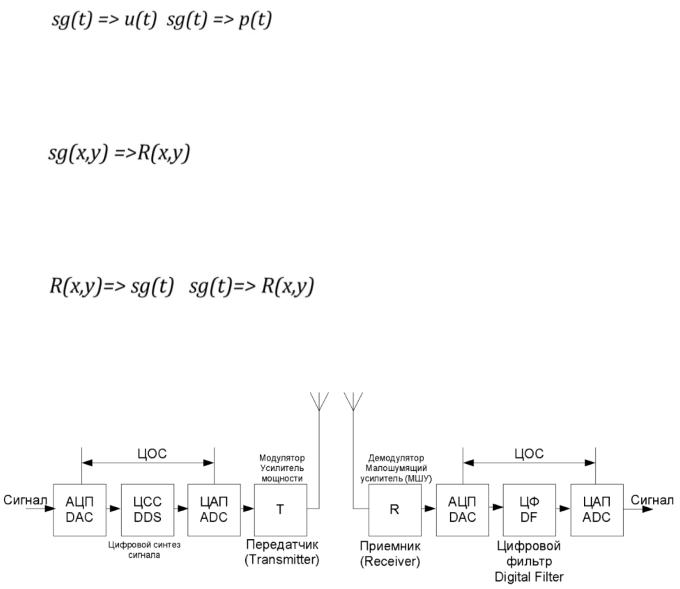
Цифровая Обработка Сигнала (ЦОС) - Digital Signal Processing (DSP)
Сигнал - изменение некоторой физической величины, несущее информацию.
Запись означает, что иногда о сигнале говорят, как о изменении напряжения u(t), а иногда как о изменении мощности p(t) во времени.
Может быть так, что аргументом являются пространственные координаты (изменение яркости в пространстве). Такой сигнал называют Изображением.
R - яркость свечения
Переход от Изображения к временному сигналу, это, например, телевизионный передатчик. А переход от временного сигнала к Изображению это телевизионный приемник:
Цифровая обработка подразумевает следующие этапы работы
●Упрощённая версия:
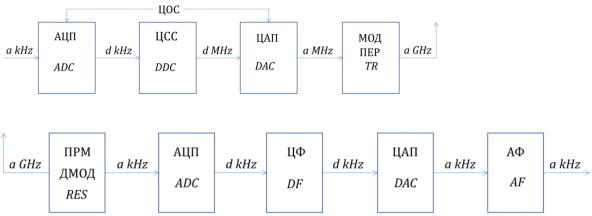
●Версия из лекции с учетом изменения мощности сигнала:
a - аналоговый сигнал d - цифровой сигнал Стрелочки вверх - антенны передатчика и приёмника
Аналого-Цифровой Преобразователь(АЦП) - Analog-Digital Converter (ADC)
Цифровой синтез сигнала (ЦСС) - Direct Digital Synthesis (DDS)
Цифро-Аналоговый Преобразователь (ЦАП) - Digital-Analog Converter (DAC) Модулятор, Передатчик (ПДР) - Transmitter (TR)
Демодулятор, Приемник (ПРМ) - Receiver (RES)
Цифровой Фильтр (ЦФ) - Digital Filter (DF)
Аналоговый фильтр (АФ) - Analog Filter (AF)
Применение ЦОС в системах связи
●Системы связи с кодовым разделением
Сраспространением радио возникла проблема – разделение каналов. Телевидение и сотовая связь только усугубили положение. В связи с этим на смену старым технологиям пришла система связи с кодовым разделением:
Code Division Multiple Access (CDMA) - технология мобильной связи, при которой
каналы передачи имеют общую полосу частот, но разную кодовую модуляцию.
Происходит кодовое разделение каналов. Каждому абоненту отводится свой код. Сигналы, используемые при этом, несут шумоподобный характер. Приемник, настроенный на определенный код, способен выделять из общего шума ту часть, которая предназначена именно ему.
При такой технологии нет временного и частотного разделения. Каждый абонент использует всю ширину канала, передавая сигнал в общий частотный диапазон
Плюсы такого метода:
●Гибкое распределение ресурсов - при кодовом разделении нет строгого
ограничения на число каналов. С увеличение числа абонентов возрастает
вероятность ошибок декодирования, но это не ведет к отказу обслуживания.
●Высокая спектральная эффективность - кодовое разделение позволяет
обслужить больше абонентов на той же полосе частот, чем другие виды
разделения (FDMA, TDMA)
●Более защищенные каналы - выделить нужный канал без знания его кода весьма трудно. Вся полоса частот равномерно заполнена шумоподобным сигналом
До CDMA также существовали технологии:
FDMA - Frequency Division Multiple Access (метод множественного доступа с частотным разделением)
TDMA - Time Division Multiple Access (метод множественного доступа с временным разделением)
Теорема Котельникова (она же теорема Найквиста-Шеннона или теорема отсчетов): если аналоговый сигнал x(t) имеет ограниченный спектр, то он может быть восстановлен однозначно и без потерь по отсчетам, только если взят с частотой строго большей удвоенной максимальной частоты спектра.
Звук содержит частоты от 20Гц до 20кГц, по теореме Котельникова частота оцифровки должна быть как минимум в два раза больше.
● Шумоподобные сигналы. Коды Баркера
Очевидно, что коды, когда их много, в эфире создают шум.
Коды Баркера хороши тем, что при цифровой обработке, не создают собственных дополнительных шумов (далее - имеют маленькие боковые пики). Другие виды кодов с
этим справляются гораздо хуже.
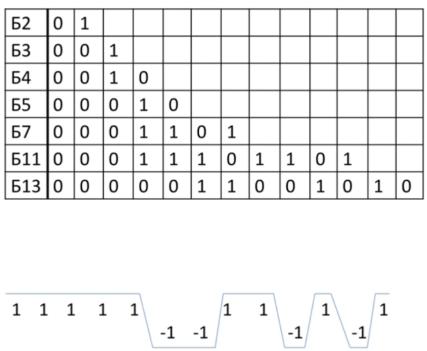
Наиболее знаменитые коды Баркера:
1.Если заменить в кодах 0 на +1, а 1 на -1, то получится знакопеременный ряд,
похожий на так называемый ЛЧМ-сигнал (линейно-частотно модулированный
сигнал), например:
2. М-последовательности.
Коды максимальной длины или М-последовательности.
Буква М как раз говорит, о их максимальности. При заданном исходном числе, М-последовательность обеспечивает максимальную длину кода.
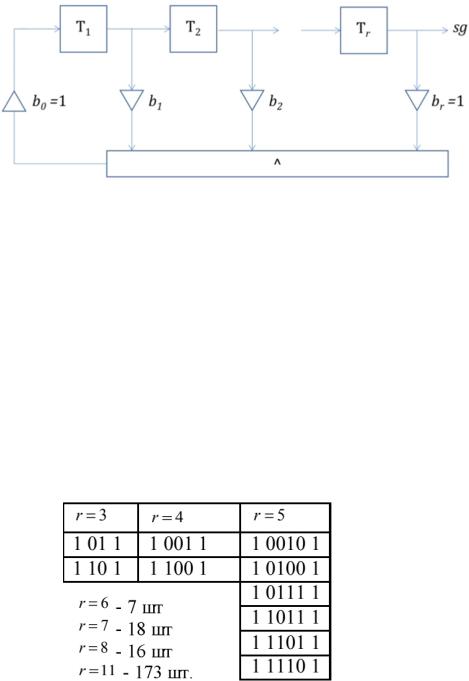
М-последовательность формируется с помощью цифрового автомата:
- сдвиговый
регистр |
|
1,..., |
|
1,..., −1ϵ {0, 1} |
- |
|
|
умножители |
|
^ - умножение по модулю
2
Если коэффициенты 0,..., образуют неприводимый многочлен r-го порядка
относительно некоторой переменной X, то нарисованная схема формирует
максимально возможную последовательность длины − 1
Многочлен: |
( ) = |
0 |
0 |
+ 1 |
1 |
+... + |
. Первый и последний член ( |
0, |
|
) всегда |
равны 1. |
|
|
0 |
|
|
Многочлен называется неприводимым, если его нельзя получить из другого
многочлена с помощью линейных процедур. Неприводимый многочлен - многочлен, не разлагающийся на множители более низкой степени.
Неприводимые многочлены низкой степени:
Такие многочлены как раз и позволяют создать М-последовательность
максимальной длины − 1
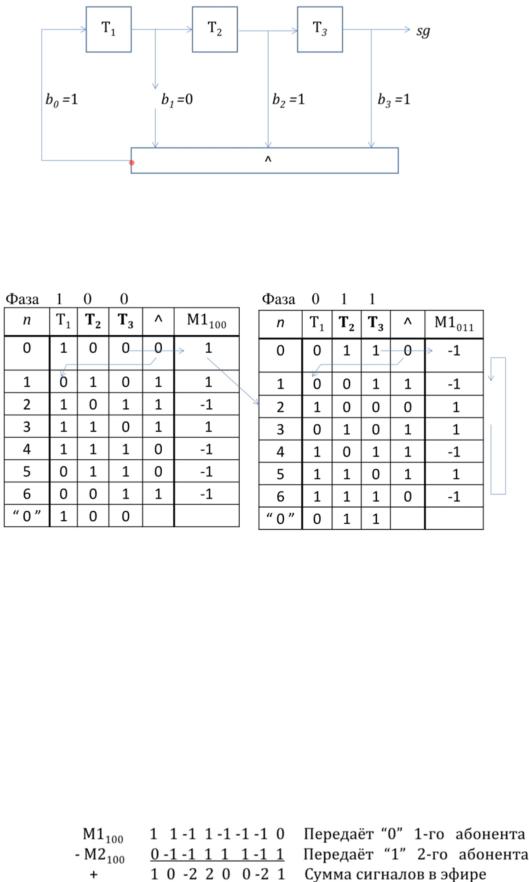
Пример формирования М-последовательности
r = 3, Многочлен М1 = 1011
1.Строим схему в соответствии с кодом:
Начальная фаза, то есть начальные значения регистров1,..., , могут быть любыми,
только если это не оговорено в условии задачи.
Например:
{ 1 2 3} = {1, 0, 0} или { 1 2 3} = {0, 1, 1}
2.Производим начальную установку регистров и прогоняем через него значения, пока фаза не вернётся к своему начальному состоянию.
Как мы видим, при разной начальной фазе результат получается один и тот же, учитывая смещение.
Но если бы мы поменяли многочлен0,..., 3, то М-послед.
была бы уже другой!!!
Описание столбцов:
●n - номер итерации
●T1, T2, T3- значение регистров
●^ - сложение по модулю 2 (учитываются только те ячейки триггеров, в которых значение многочлена 0,..., равно 1, в таблице имена этих триггеров
выделены жирным)
●M1 - сама М-последовательность, сюда попадают значения из старшего регистра (см. схему) и переводятся в знакопеременный код (0 заменяется на +1,
а 1 на -1,)
Заключение
Если бы послали две разные М-последовательности в эфир, то в результате получили
бы их смесь. Фильтрация таких сигналов дается в следующем билете.
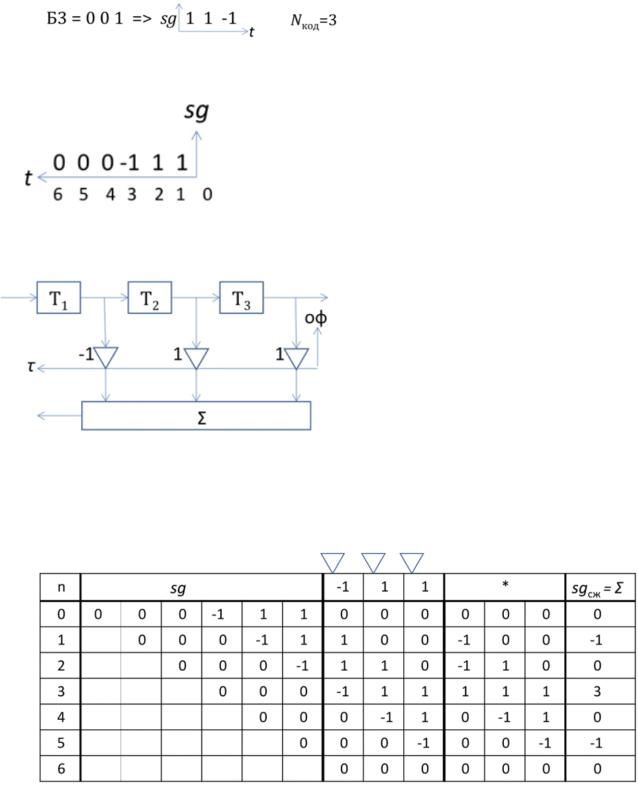
3. Фильтрация ШПС-сигналов. АКФ, ВКФ М-последовательностей.
Фильтрация ШПС-сигналов
ШПС - шумоподобный сигнал, например, коды Баркера(см. вопрос №1)
Пример 1. Возьмём сигнал Баркер-3 (Б3) и сделаем его знакопеременным:
Теперь просто для удобства дальнейшей работы, развернем этот сигнал и припишем в начале три нуля.
Кол-во нулей не имеет значения, они нужны только для того, чтобы увидеть полную картину отфильтрованного сигнала, т.к. в реальной ситуации сигналы много длинней и, обычно, многократно повторяются.
Фильтрацию производим с помощью согласованного, или оптимального фильтра:
Длина фильтра (кол-во регистров) равна длине кода ф = код
ОФ - опорная функция.
Опорная Функция должна быть согласована с тем сигналом, который мы фильтруем, отсюда и название фильтра,
как согласованного
Первоначально регистры 1,..., пусты и имеют значение 0
Теперь запускаем сдвиговый регистр и слева направо пропускаем через него sg
сигнал, наблюдаем за процессом:
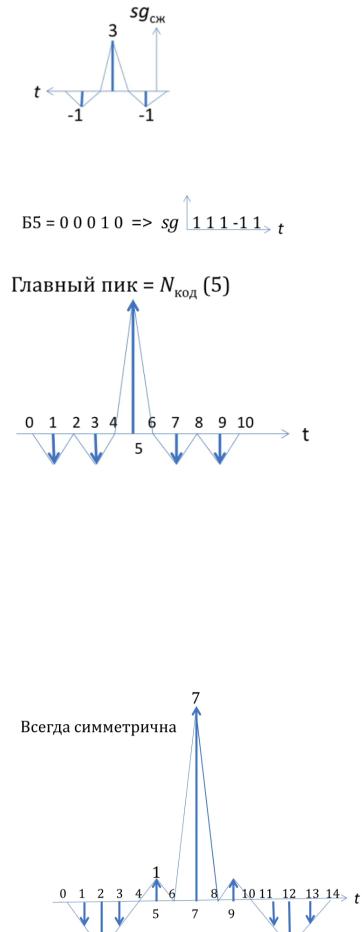
В каждой итерации после очередного сдвига заполняются столбцы умножения “ * ” - значения из сдвигового регистра почленно умножаются на Опорную Функцию и заносятся в соответствующие ячейки.
Последний столбец, сумма перемноженных значений - есть
сжатый сигнал сж
Пик, равный 3-м, говорит об успешной фильтрации сигнала. Ответвления -1, хоть немного и мешают, внося шум, но сами по себе значительно меньше пика
Пример 2. На этот раз возьмём код Баркера-5 (Б5)
Проделав аналогичную примеру 1 операцию, получим следующий результат:
Главный пик в идеальном случае(когда нет смеси сигналов) равняется длине сигнала, в данном случае 5-ти.
В этом примере можно увидеть полезную отличительную особенность кодов Баркера - их боковые пики минимальны(в примере равны 1-му), или, иначе говоря, коды Баркера обладают идеальной Авто-Корреляционной
Функцией.
АКФ, ВКФ М-последовательности
Авто-Корреляционная Функция (АКФ) - функция, оценивающая похожесть сигнала на самого себя. (лат correlаtio - взаимодействие). По сути это и есть процесс
фильтрации, после которого, наблюдая за пиками, мы можем судить о том,
правильный ли пришёл сигнал, или ложный.
Пример АКФ для М-последовательности: M1(100)
(Построение М-посл. см. Вопрос №2)
Боковые пики М-посл. хуже, чем у кодов Баркера, но М-посл значительно выигрывает в длине кода.
АКФ всегда симметрична Главный пик равен длине кода Боковые пики подчиняются
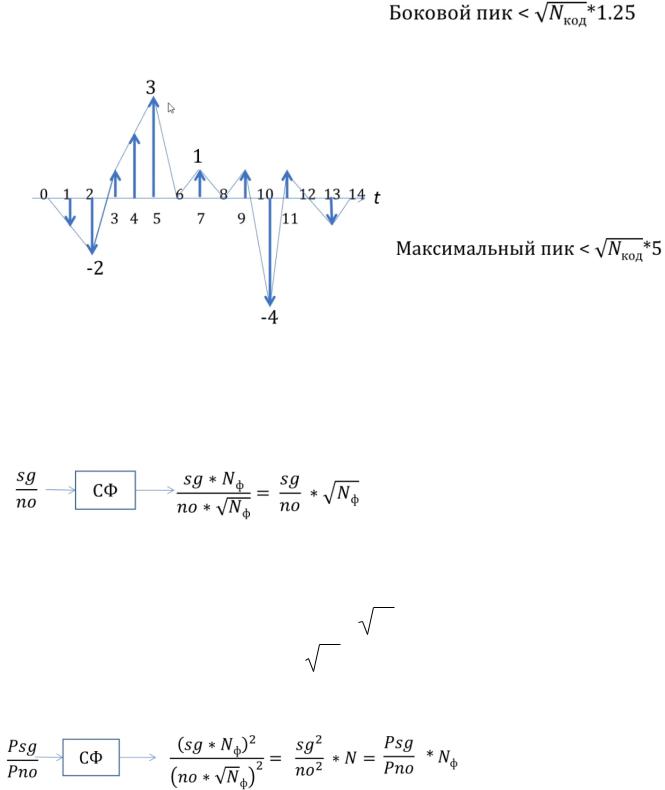
неравенству(ограничение Варакина):
ВзаимноКорреляционная Функция (ВКФ) -
Аналогично АКФ, но для смеси двух или более сигналов, например для смеси двух М-последовательностей:
Пика теперь два, и они совершенно не обязательно равны длине начального сигнала
Для ВКФ также существует
ограничение Варакина, уже для максимального пика:
Важным моментом является то, что чем больше длина кода, тем менее значимы боковые пики, а сигнал, соответственно, становится “чище”.
Но есть еще одно обстоятельство. Кроме собственных сигналов, есть ещё некоторый независимый шум в системе связи.
Рассмотрим выражение:
sg - сигнал
no - шум системы связи
СФ - согласованный фильтр
Что же происходит после прохождения фильтра?
●Сигнал увеличит свою амплитуду в фраз
● Шум no увеличит амплитуду примерно в |
|
фраз |
Таким образом отношение увеличится в фпо |
уровню, а это хорошо :) |
|
|
|
|
Но также существует аналогичное выражение для мощности:
Psg - мощность сигнал
Pno - мощность шума системы связи
Здесь ситуация ещё более ощутима, так как отношение возрастает в фраз.
Заключение.
