
- •Определенный интеграл Римана. Эквивалентные определения. Условие Коши.
- •Ограниченность интегрируемой функции.
- •Суммы Дарбу. Их Свойства.
- •Суммы Дарбу и интегрируемость функции по Риману.
- •Билет 41 Основная теорема о существовании определенного интеграла Римана.
- •Равномерная непрерывность функции. Модуль непрерывности.
- •Теорема 2 Функция непрерывная на отрезке, равномерно непрерывна на нем ().
- •Интегрируемость по Риману непрерывной функции.
- •Интегрируемость по Риману монотонной функции.
- •Аддитивное и однородные свойства определенного интеграла Римана.
- •Неравенства для определенного интеграла Римана и теорема о среднем.
- •Интеграл как функция верхнего предела. Непрерывность и дифференцируемость. Теорема Ньютона-Лейбница.
- •Билет 48 Определение площади. Площадь криволинейной трапеции. Площадь в полярных координатах.
- •Определение объёма. Объем тела вращения.
- •Длина дуги кривой. Определение и вычисление.
Неравенства для определенного интеграла Римана и теорема о среднем.
Теорема 1:
Если
функции
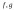 интегрируемы на
интегрируемы на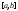 и
и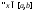
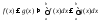
Доказательство:
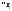 выполняется
неравенство
выполняется
неравенство
 ,
тогда
,
тогда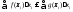 .
Так как интегралы по условию существуют,
по теореме о предельном переходе под
знаком неравенства,
.
Так как интегралы по условию существуют,
по теореме о предельном переходе под
знаком неравенства,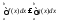 .
Теорема доказана.
.
Теорема доказана.
Следствие:
Если
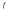 -
интегрируема на
-
интегрируема на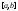 ,
то, по доказанному выше,
,
то, по доказанному выше,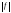 - интегрируем на данном отрезке; тогда
- интегрируем на данном отрезке; тогда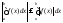
Доказательство:
Известно
неравенство:
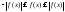 ; по данной теореме
; по данной теореме
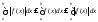 ;
из самого правого интеграла минус можно
вынести; получим:
;
из самого правого интеграла минус можно
вынести; получим:
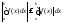 .
Следствие доказано.
.
Следствие доказано.
Теорема 2: (о среднем)
Пусть
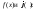 интегрируемы
на
интегрируемы
на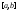 ,
причем
,
причем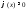 на данном промежутке, тогда
на данном промежутке, тогда
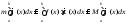 ,
где
,
где
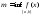 ,
,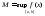
и
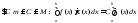
Замечание: sup и inf существуют, т.к. функция на данном промежутке интегрируема, а значит ограничена.
Доказательство:
Запишем
неравенство:
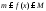 и домножим его на
и домножим его на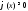 :
:
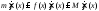 ;
тогда по теореме о неравенствах это
неравенство сохранится и в интегралах:
;
тогда по теореме о неравенствах это
неравенство сохранится и в интегралах:
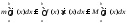 (
( )
)
Если
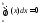 ,
то и интеграл
,
то и интеграл и неравенство (
и неравенство ( )
выполняется.
)
выполняется.
Если
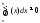 ,
тогда по теореме о неравенствах
,
тогда по теореме о неравенствах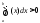 ,
значит можно неравенство (
,
значит можно неравенство ( )
на него разделить:
)
на него разделить:
 и принимаем за
и принимаем за
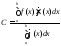 .
Теорема доказана.
.
Теорема доказана.
Следствие:
Если
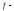 непрерывна
на
непрерывна
на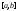 и выполняется условие теоремы, то
и выполняется условие теоремы, то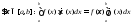
Доказательство:
Т.к.
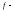 непрерывна
на
непрерывна
на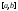 ,
то она достигает своегоmax
и min
значения, а в силу непрерывности sup=max,
inf=min;
значит
,
то она достигает своегоmax
и min
значения, а в силу непрерывности sup=max,
inf=min;
значит
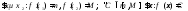 - по теореме о промежуточных значениях
непрерывной функции. Следствие доказано.
- по теореме о промежуточных значениях
непрерывной функции. Следствие доказано.
Следствие к следствию:
Если
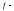 непрерывна
на
непрерывна
на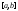 ,
то
,
то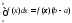
Доказательство:
Возьмем
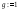 ,
тогда
,
тогда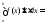 (по
следствию)
(по
следствию)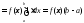 .
Следствие доказано.
.
Следствие доказано.
Геометрический
смысл этого следствия:
Если считать
площадь криволинейной трапеции, то
найдется такая точка
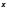 ,
что площадь этой криволинейной трапеции
будет равна площади прямоугольника с
высотой
,
что площадь этой криволинейной трапеции
будет равна площади прямоугольника с
высотой .
.
Билет 47
Интеграл как функция верхнего предела. Непрерывность и дифференцируемость. Теорема Ньютона-Лейбница.
Рассмотрим функцию
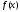 ,
интегрируемую на отрезке
,
интегрируемую на отрезке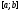 .
По аддитивному свойству интеграла:
.
По аддитивному свойству интеграла:
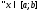 ,
можно найти отрезок
,
можно найти отрезок
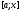 на котором представляется возможным
рассмотреть функцию
на котором представляется возможным
рассмотреть функцию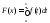 .
.
Теорема:
Если функция
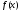 интегрируема на отрезке
интегрируема на отрезке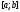 ,
то
,
то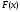 непрерывна на отрезке
непрерывна на отрезке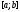 .
.
Доказательство:
Рассмотрим функцию
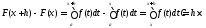 ,
,
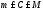 ,
где
,
где
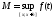 ,
,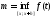 ,
,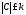 ,
где
,
где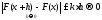
Теорема доказана.
Теорема:
Пусть функция
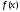 интегрируема на отрезке
интегрируема на отрезке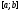 ,
непрерывна в точке
,
непрерывна в точке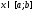 ,
тогда функция
,
тогда функция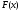 дифференцируема в точке
дифференцируема в точке и
и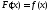 .
.
Доказательство:
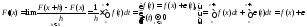 ,
,
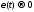 ,
,
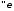
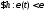
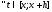 ,
т.е.
,
т.е.
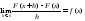 .
.
Теорема доказана.
Следствие:
Если функция
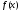 непрерывна на отрезке
непрерывна на отрезке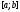 ,
то
,
то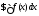 ,
т.е.
,
т.е.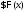 - первообразная
- первообразная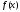 .
.
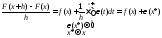 ,
,
Функция
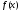 непрерывна в точке
непрерывна в точке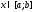 ,
,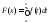 ;
;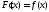 ,
где
,
где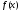 непрерывна на отрезке
непрерывна на отрезке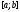 .
Заключаем, что
.
Заключаем, что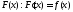 .
.
Т.е. любая непрерывная функция имеет первообразную.
Теорема доказана.
Формула Ньютона-Лейбница:
Функция
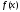 непрерывна на отрезке
непрерывна на отрезке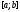 ,
тогда она имеет первообразную. Пусть
,
тогда она имеет первообразную. Пусть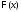 - её произвольная первообразная. Тогда
- её произвольная первообразная. Тогда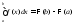 .
.
Доказательство:
Функция
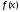 непрерывна на отрезке
непрерывна на отрезке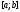 ,
,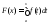 - первообразная функции
- первообразная функции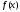 ,
,
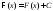 ,
,
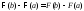 ,
,
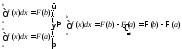 . Теорема
доказана.
. Теорема
доказана.
Билет 48 Определение площади. Площадь криволинейной трапеции. Площадь в полярных координатах.
Определение:
Пусть множество
 и A
– ограничено. Рассмотрим множество
и A
– ограничено. Рассмотрим множество
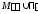 (объединение прямоугольников), такое
что
(объединение прямоугольников), такое
что ,
и множество
,
и множество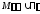 ,
такое что
,
такое что ,
и назовем
,
и назовем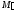 и
и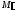 фигурами. Площади этих фигур
фигурами. Площади этих фигур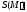 и
и![]() можно
посчитать. Т.к. множество
можно
посчитать. Т.к. множество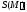 оганичено
сверху (S(A))
оганичено
сверху (S(A))![]() .
Аналогично
.
Аналогично![]() ограничено снизу (нулем)
ограничено снизу (нулем)![]() .
Если
.
Если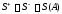 ,
то это площадьA,
а множество называется квадрируемым.
,
то это площадьA,
а множество называется квадрируемым.
Пример1:
Пусть τ – отрезок и
![]() .
.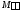 Ø.
При этомS(M΄)=0
и
Ø.
При этомS(M΄)=0
и
![]() .
Пусть длина отрезка равнаd,
тогда
.
Пусть длина отрезка равнаd,
тогда
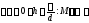 ,
а
,
а![]() длиныd
и высоты h.
Тогда
длиныd
и высоты h.
Тогда
![]() .
ПолучилиS(τ)=0.
.
ПолучилиS(τ)=0.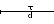
Пример2:
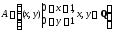 .
. ,
,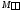 Ø
и
Ø
и![]() ,
т.к. никакой прямоугольник полностью
не лежит в этом множестве.
,
т.к. никакой прямоугольник полностью
не лежит в этом множестве. ,
т.е.
,
т.е.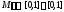 ,
поэтому
,
поэтому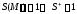 .
Получаем, что
.
Получаем, что![]() ,
поэтому множествоA
- не квадрируемое.
,
поэтому множествоA
- не квадрируемое.
Пусть f(x)≥0 на [a,b]. Криволинейная трапеция T - множество (x,y), такое что a≤x≤b и 0≤y≤f(x).
Теорема: (О площади криволинейной трапеции).
Пусть
функция f(x)≥0
на [a,b].
Криволинейная трапеция T
квадрируема тогда и только тогда(),
когда функция f(x)
интегрируема на [a,b].
При этом площадь T
равна:
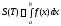 .
.
Доказательство:
:
По основной теореме
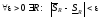 .
Найдутся такие
.
Найдутся такие
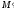 и
и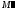 ,
что
,
что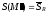 и
и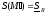 .
Тогда
.
Тогда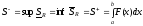 .
.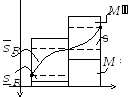
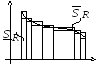
:
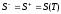 ,
так как криволинейная трапецияT
квадрируема. Тогда
,
так как криволинейная трапецияT
квадрируема. Тогда
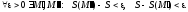
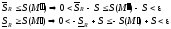 Обе интегральные суммы стремятся к
одному и тому же числу (S).
Обе интегральные суммы стремятся к
одному и тому же числу (S).
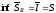 ,
,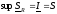 .
Следовательно
.
Следовательно ,
поэтому функцияf(x)
интегрируема (из следствия основной
теоремы).
,
поэтому функцияf(x)
интегрируема (из следствия основной
теоремы).
Пример.
x2+y2=R2.
a≤x≤b
(a=-R,
b=R),
и 0≤y≤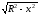 .
При этом
.
При этом
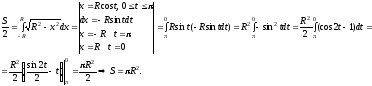
Замечание
к определению площади:
Множества
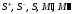 можно заменить на любые другие квадрируемые
множества. Если
можно заменить на любые другие квадрируемые
множества. Если![]() - фигуры,
- фигуры,![]() - квадрируемые множества, т.е. существуют
площади
- квадрируемые множества, т.е. существуют
площади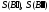 и при этом
и при этом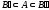 ,
то при
,
то при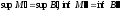 получим все то же самое.
получим все то же самое.
Пусть множество
задано в полярных
координатах:
x=r·cost,
y=r·sint.
Рассмотрим множество A,
такое, что α≤t≤β
и 0≤r≤r(t).
Введем разбиение угла [α,β]:
α=t0<t1<t2<…<tn=β.
При этом Δti=[ti
,ti+1].
Рассмотрим сектора окружностей ri=mi
– это будут сектора
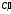 иri=Mi
– это будут сектора
иri=Mi
– это будут сектора
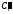 .
.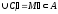 и
и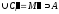 .
Окружности (с углом 2π) соответствует
площадьπR2,
а сектору с углом α – площадь αR2/2.
Поэтому
.
Окружности (с углом 2π) соответствует
площадьπR2,
а сектору с углом α – площадь αR2/2.
Поэтому
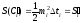 и
и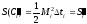 .
.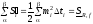 и
и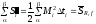 -
нижняя и верхняя суммы Дарбý для функцииf=r2/2.
Получим
-
нижняя и верхняя суммы Дарбý для функцииf=r2/2.
Получим
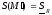 и
и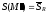 .
То есть площадьS(A)
существует и равна S
(т.е. A
квадрируема) тогда и только тогда, когда
существует интеграл
.
То есть площадьS(A)
существует и равна S
(т.е. A
квадрируема) тогда и только тогда, когда
существует интеграл
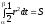
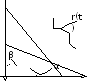
Билет 49
