
- •Определенный интеграл Римана. Эквивалентные определения. Условие Коши.
- •Ограниченность интегрируемой функции.
- •Суммы Дарбу. Их Свойства.
- •Суммы Дарбу и интегрируемость функции по Риману.
- •Билет 41 Основная теорема о существовании определенного интеграла Римана.
- •Равномерная непрерывность функции. Модуль непрерывности.
- •Теорема 2 Функция непрерывная на отрезке, равномерно непрерывна на нем ().
- •Интегрируемость по Риману непрерывной функции.
- •Интегрируемость по Риману монотонной функции.
- •Аддитивное и однородные свойства определенного интеграла Римана.
- •Неравенства для определенного интеграла Римана и теорема о среднем.
- •Интеграл как функция верхнего предела. Непрерывность и дифференцируемость. Теорема Ньютона-Лейбница.
- •Билет 48 Определение площади. Площадь криволинейной трапеции. Площадь в полярных координатах.
- •Определение объёма. Объем тела вращения.
- •Длина дуги кривой. Определение и вычисление.
Равномерная непрерывность функции. Модуль непрерывности.
Определение
1:
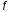 ограниченная
ограниченная
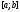 функция,
функция,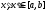 и
и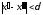 при выполнении условия
при выполнении условия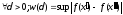 ,
,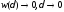 называется равномерно непрерывной.
называется равномерно непрерывной.
Определение
2(Критерий Коши):
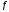 - равномерно непрерывная функция на
отрезке
- равномерно непрерывная функция на
отрезке
 если выполняется условие
если выполняется условие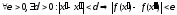 при
при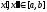 .
.
Теорема 1 (Эквивалентность определений 1 и 2)
Доказательство:
Так как
 и
и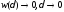 выполняется
Критерий Коши.
выполняется
Критерий Коши.
Теорема 2 Функция непрерывная на отрезке, равномерно непрерывна на нем ().
Доказательство:
Допустим что теорема неверна. Построим отрицание к определению 2.
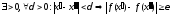 .
Зададим стремящуюся к нулю последовательность
положительных чисел
.
Зададим стремящуюся к нулю последовательность
положительных чисел
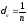 ,
тогда
,
тогда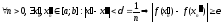 .
Так как точки последовательности
.
Так как точки последовательности принадлежат к отрезку
принадлежат к отрезку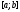 ,
то эта последовательность ограничена,
и из нее можно выделить, по теореме
Больцано-Вейерштрасса, подпоследовательность
,
то эта последовательность ограничена,
и из нее можно выделить, по теореме
Больцано-Вейерштрасса, подпоследовательность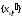 ,
сходящуюся к некоторой точке
,
сходящуюся к некоторой точке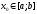 .
Значит, из нее можно выделить также
подпоследовательность
.
Значит, из нее можно выделить также
подпоследовательность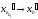 .
Аналогично выделим подпоследовательность
.
Аналогично выделим подпоследовательность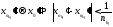 и
и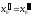
 .
Получили противоречие – теорема
доказана.
.
Получили противоречие – теорема
доказана.
Необходимость
условия:
Если
 ,
то теорема 2 не выполняется.
,
то теорема 2 не выполняется.
Пример
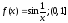 Пусть
Пусть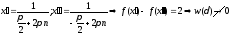 при
при .
.
Билет 43
Интегрируемость по Риману непрерывной функции.
Теорема 1:
Если функция
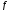 непрерывна на
непрерывна на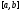 ,
то она интегрируема на
,
то она интегрируема на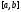 .
.
Доказательство:
Пусть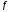 непрерывна на
непрерывна на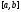 ;
тогда для разбиенияR,
у которого частичные отрезки
;
тогда для разбиенияR,
у которого частичные отрезки
 ,
имеет место (
,
имеет место ( ).
).
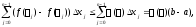
где
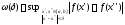 есть модуль непрерывности
есть модуль непрерывности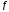 на
на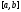 .
.
Поэтому
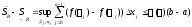 .
.
Но, как мы знаем,
для непрерывной на замкнутом конечном
отрезке
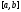 функции
функции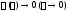 ,
поэтому для любого
,
поэтому для любого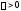 можно указать такое
можно указать такое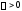 ,
что
,
что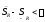 .
.
В силу основной
теоремы интеграл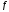 на
на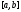 существует.
существует.
Теорема доказана.
Билет 44
Интегрируемость по Риману монотонной функции.
Теорема 1:
Если
функция монотонна на отрезке
 ,
то она интегрируема на этом отрезке.
,
то она интегрируема на этом отрезке.
Доказательство:
Возьмем
произвольное разбиение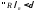
Рассмотрим
разность между верхней и нижней суммой
Дарбу, пусть для определенности f
не убывает на
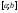 ,
тогда мы получим, что
,
тогда мы получим, что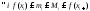
Получим, что разность между верхней и нижней суммой Дарбу
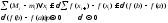
Теорема доказана.
Билет 45
Аддитивное и однородные свойства определенного интеграла Римана.
Теорема 1: (Аддитивное свойство интегралов)
Функция
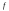 интегрируема на отрезке
интегрируема на отрезке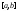 тогда и только тогда, когда
тогда и только тогда, когда функция
интегрируема на отрезках
функция
интегрируема на отрезках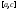 и
и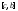 и при этом выполняется равенство:
и при этом выполняется равенство: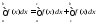
Доказательство:
 Пусть
Пусть
 интегрируема на
интегрируема на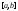 ,
тогда по основной теореме
,
тогда по основной теореме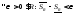
Можно
считать, что точка c
является точкой разбиения, потому что,
если она таковой не является, мы добавим
эту точку и рассмотрим новое разбиение
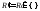 ,
тогда
,
тогда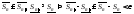 ,
поэтому можно считать, что разбиениеR
изначально содержит точку с. Тогда это
разбиение порождает разбиения
,
поэтому можно считать, что разбиениеR
изначально содержит точку с. Тогда это
разбиение порождает разбиения
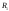 -
разбиение
-
разбиение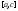 и
и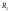 -
разбиение
-
разбиение .
Тогда
.
Тогда и разность сумм Дарбу можно представить
как:
и разность сумм Дарбу можно представить
как:
 .
Так как каждое из этих двух слагаемых
неотрицательно и в сумме они меньше
.
Так как каждое из этих двух слагаемых
неотрицательно и в сумме они меньше
 ,
значит каждое из них меньше
,
значит каждое из них меньше
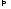 по
основной теореме
по
основной теореме интегрируема на
интегрируема на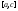 и
и .
Доказано.
.
Доказано.
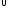 Пусть
Пусть
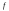 интегрируема на отрезках
интегрируема на отрезках и
и ,
тогда точно так же найдем
,
тогда точно так же найдем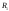 -
разбиение
-
разбиение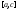 и
и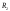 -
разбиение
-
разбиение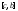 ,
такие что
,
такие что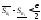 и
и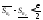 ,
тогда для разбиения
,
тогда для разбиения
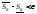 ,
гдеR–разбиение
отрезка
,
гдеR–разбиение
отрезка
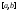 ,
,
значит
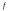 интегрируема на отрезке
интегрируема на отрезке .
Доказано.
.
Доказано.
Доказали
интегрируемость, теперь докажем равенство
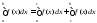 :
:
Замечание: Мы предполагаем, что точка с участвует во всех этих разбиениях; если она в них не участвует, то по следствию из основной теоремы нам это неважно, поскольку если хотя бы для одной последовательности разбиений предел стремится к числу, то и для всех остальных - тоже. И мы берем такую последовательность разбиений, что точка с в них участвует.
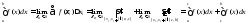
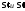 - сумма берется по
тем отрезкам, которые содержатся в
- сумма берется по
тем отрезкам, которые содержатся в
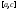 и
и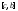 соответственно. Нужно учесть, что
соответственно. Нужно учесть, что .
Теорема доказана.
.
Теорема доказана.
Замечание:
Мы определили понятие определенного
интеграла только для случая
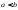 ;
доопределим понятие определенного
интеграла отa
до b
в случае, когда
;
доопределим понятие определенного
интеграла отa
до b
в случае, когда
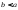 :
:
Если
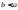 ,
то положим
,
то положим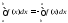 ,
тогда равенство
,
тогда равенство становится верным не только для
становится верным не только для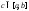 ,
но и для любых
,
но и для любых ,
при условии что все вышеперечисленные
интегралы существуют.
,
при условии что все вышеперечисленные
интегралы существуют.
Пример:
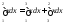
Теорема2: (Однородные свойства интегралов)
Пусть
функции
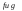 интегрируемы
на
интегрируемы
на ,
тогда
,
тогда
f + g – интегрируема на
 и
и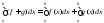 ,
если интегралы в правой части существуют,
т.е. в общем случае обратное не верно.
,
если интегралы в правой части существуют,
т.е. в общем случае обратное не верно.
(Пример:
Если взять f
– неинтегрируема на
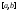 и –f
– тоже неинтегрируема, то их сумма =0 –
интегрируема).
и –f
– тоже неинтегрируема, то их сумма =0 –
интегрируема).
 - интегрируема на
- интегрируема на
 и
и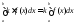 ,
обратное тоже верно, в случае если
,
обратное тоже верно, в случае если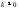
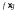 - интегрируема.
- интегрируема.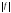 - интегрируем
- интегрируемЕсли
 отделена от 0 на отрезке
отделена от 0 на отрезке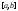 ,
т.е.
,
т.е.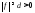 на
на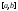 где
где ,
то
,
то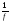 - интегрируема.
- интегрируема.
Доказательство:
1)

2) аналогично;
Замечание:
обозначим
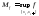 ;
;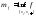 ;
;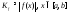 - по свойству ограниченности; соответственно
введем
- по свойству ограниченности; соответственно
введем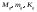
3)
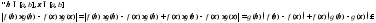

Перейдем
к супремумам: на произвольном промежутке
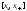

По
основной теореме найдутся такие разбиения
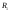 ,
что
,
что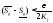 и
и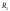 ,
что
,
что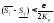 .
Теперь если мы возьмем сумму разбиений
.
Теперь если мы возьмем сумму разбиений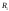 и
и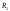 ,
то будут выполняться оба неравенства,
и тогда
,
то будут выполняться оба неравенства,
и тогда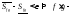 интегрируема.
интегрируема.
4)
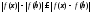 ;
переходя к супремумам и умножая на
;
переходя к супремумам и умножая на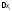 ,
получим:
,
получим:
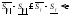
Замечание:
переход к супремуму на промежутке
 :
: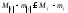
Замечание: обратное неверно:
Контрпример:
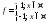 - сама по себе не интегрируема (доказано
ранее), а по модулю – интегрируема.
- сама по себе не интегрируема (доказано
ранее), а по модулю – интегрируема.
5)
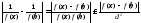 ;
переходя к супремумам супремум в этом
неравенстве, получим:
;
переходя к супремумам супремум в этом
неравенстве, получим:
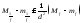 ;
теперь домножая на
;
теперь домножая на
 и суммируя, получим
и суммируя, получим
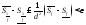
Теорема доказана.
Билет 46
