73

Лекция 7

Числовые характеристики случайных величин. Математическое ожидание, дисперсия, среднее квадратичное отклонение, начальные и центральные моменты, мода и медиана.

5. Числовые характеристики случайных величин

Функция распределения полностью характеризует случайную величину. Действительно, функция распределения одновременно указывает на то, какие значения может принимать случайная величина и с какими вероятностями. С точки зрения наблюдателя, две случайные величины, имеющие одинаковые функции распределения, неразличимы, несмотря на то что они могут быть заданы на разных вероятностных пространствах и описывать разные явления. Так, например, при игре в "орлянку" все равно, какая монета бросается. Однако составить полное представление о случайной величине только по функции распределения бывает часто довольно трудно. Еще труднее сравнивать случайные величины. В связи с этим вводят более простые характеристики случайной величины, определяемые только одним числом. Хотя числовые характеристики не дают полного представления о случайной величине, однако они в сжатой форме выражают наиболее важные черты распределения. Числовые характеристики играют большую роль в теории вероятностей и ее приложениях. Основную роль на практике играют – математическое ожидание, характеризующее "центральное" значение случайной величины, и дисперсия, характеризующая "разброс" вокруг математического ожидания. Среди остальных характеристик можно выделить те, которые применяются в специальных вероятностных дисциплинах (например, квантили широко используются в математической статистике), и те, которые носят ярко выраженный теоретический характер (например, моменты высших порядков).

5.1. Математическое ожидание

Одной из важнейших и, в тоже время, наиболее простой характеристикой случайной величины является математическое ожидание. Введение математического ожидания тесно связано с понятием среднего арифметического значения, используемого в математической статистике. В связи с этим вместо термина "математическое ожидание" используется термин "среднее значение". Отметим также, что математическое ожидание имеет аналог и в теоретической механике. Если считать возможные значения случайной величины x_i, координатами неких точек, то математическое ожидание будет характеризовать центр тяжести такой системы точек. В связи с этим, математическое ожидание иногда называют центром распределения.

Математическое ожидание будем обозначать буквой M (отметим, что в зарубежной литературе для этого часто используется буква E, от англ. expectation – ожидание). Если нужно указать для какой случайной величины вычисляется математическое ожидание, то будем писать M[X], M(X) или M.

Математическим ожиданием ДСВ X называется сумма произведений ее возможных значений на их вероятности:

M[X] = = x₁p₁+x₂p₂+ ... +x_np_n. (5.1)

Если ДСВ X принимает бесконечное число значений, то

M[X] = ,

при условии, что этот ряд сходится абсолютно, т.е. сходится ряд:

.

В противном случае говорят, что математическое ожидание случайной величины X не существует.

Пример 5.1. Найти математическое ожидание случайных величин: X={x_n=n} и Y={y_n=(–1)n}, где n=1,2,..., если вероятности определяются по формуле

.

Решение. Непосредственно проверяется, что

.

Находим математическое ожидание случайной величины X:

M[X] = .

Поскольку полученный ряд расходится, то M[X] не существует. Далее вычисляем математическое ожидание случайной величины Y:

M[Y] = .

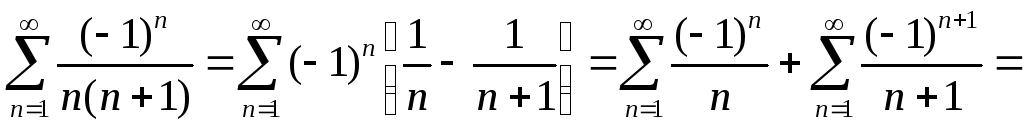
Используя разложение ln(1+x)= при x=1, получим

M[Y] = 1–2ln2.

Для определения математического ожидания НСВ X, имеющей плотность распределения f(x), заметим, допуская некоторую вольность изложения, что случайная величина X принимает значение x с вероятностью f(x)dx. Заменив сумму на интеграл, получим, что:

Математическим ожиданием НСВ X с плотностью распределения f(x) называется интеграл:

M[X] = . (5.2)

Здесь предполагается, что несобственный интеграл сходится абсолютно, т.е. существует интеграл

.

В противном случае говорят, что математическое ожидание случайной величины X не существует.

Пример 5.2. НСВ X задана плотностью распределения:

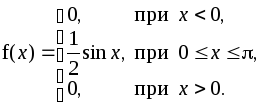
Найти математическое ожидание случайной величины X.

Решение. Поскольку f(x) при x<0 и x>0, то

.

Пример 5.3. НСВ X задана плотностью распределения Коши:

.

Найти M[X].

Решение. Распределение Коши удовлетворяет всем свойствам функции распределения, в частности:

.

Однако

,

т.е. математическое ожидание случайной величины X не существует.

В общем случае математическое ожидание случайной величины произвольной природы задается выражением

, (5.3)

где интеграл понимается в так называемом смысле Стилтьеса. Поскольку мы рассматриваем только дискретные и непрерывные случайные величины, то выражение (5.3) трактовать как обобщенную запись формул для математических ожиданий ДСВ и НСВ.

Отметим некоторые свойства математического ожидания.

Свойство 1. Математическое ожидание постоянной величины равно этой величине:

M[C] = C.

Действительно, постоянную С можно рассматривать как ДСВ, которая может принимать только одно значение C с вероятностью 1; поэтому M[C]=C1=C.

Свойство 2. Постоянный множитель можно выносить за знак математического ожидания:

M[CX] = C M[X]

Свойство 3. Математическое ожидание суммы двух случайных величин равно сумме их математических ожиданий:

M[X+Y] = M[X] + M[Y].

Свойства 2 и 3 следуют из соответствующих свойств интеграла или ряда. Здесь только отметим, что под суммой двух случайных величин X и Y понимается случайная величина X+Y, возможные значения которой равны суммам каждого возможного значения X с каждым возможным значением Y; вероятности возможных значений X+Y для независимых величин X и Y равны произведениям вероятностей слагаемых, для зависимых величин – произведениям вероятности одного слагаемого на условную вероятность другого (см. теорему об умножении вероятностей).

Свойство 4. Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий:

M[XY] = M[X]M[Y].

Свойство 4 также следует из соответствующих свойств интеграла или ряда. Здесь только отметим, что под произведением двух независимых случайных величин X и Y понимается случайная величина XY, возможные значения которой равны произведениям каждого возможного значения X с каждым возможным значением Y; вероятности возможных значений XY равны произведениям вероятностей возможных значений сомножителей.

Разность X–M[X] называется отклонением случайной величины X от ее математического ожидания. Эта разность также есть случайная величина.

Свойство 5. Математическое ожидание отклонения случайной величины от ее математического ожидания равно нулю:

M[X–M[X]] = 0.

Действительно, используя свойства математического ожидания и принимая во внимание, что M[X] – постоянная величина, получим

M[X–M[X]] = M[X]– M[M[X]] = M[X]– M[X] = 0.