95

Лекция 9

Распределения вероятностей непрерывных случайных величин. Равномерное распределение. Показательное распределение и его числовые характеристики. Функция надежности. Характеристическая функция.

7. Распределения вероятностей непрерывных случайных величин

7.1. Равномерное распределение

На практике встречаются случайные величины, о которых заранее известно, что они могут принять какое-либо значение в строго определенных границах, причем в этих границах все значения случайной величины имеют одинаковую вероятность (т.е. обладают одной и той же плотностью вероятности).

К подобным случайным величинам относится погрешность округления, например при снятии показаний с измерительных приборов, если производится округление до ближайшего целого деления. Тогда ошибка округления есть случайная величина, которая может принимать с постоянной плотностью вероятности любое значение между двумя соседними целыми делениями. Например, мы записываем значение напряжения 220 В, хотя реально это значение находится, допустим, между 215 и 225 В.

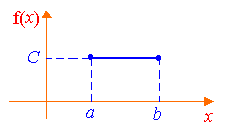
Распределение вероятностей называют равномерным, если на интервале, которому принадлежат все возможные значения случайной величины, плотность распределения постоянна:

Так как

,

то C=1/(b–a). Таким образом, плотность вероятности равномерного распределения имеет вид

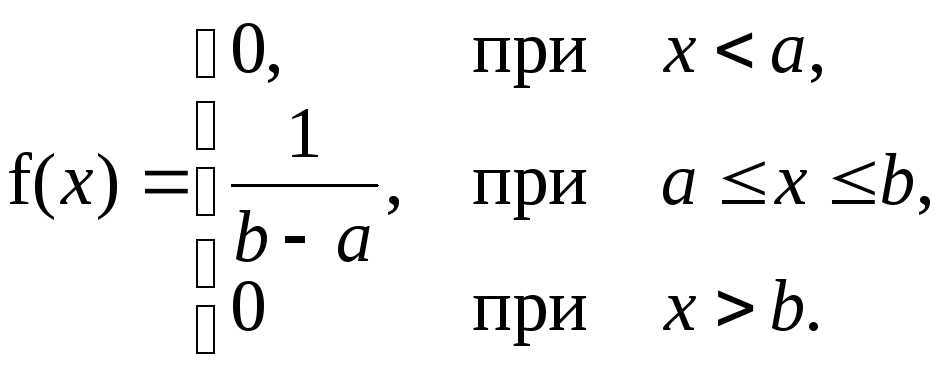(7.1)

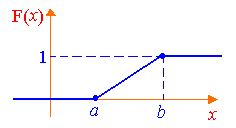
Построим функцию распределения F(x) для равномерного распределения:

.

Отметим, что при x<a функция F(x)=0 и при x>b функция F(x)=1.

Рис. 7.1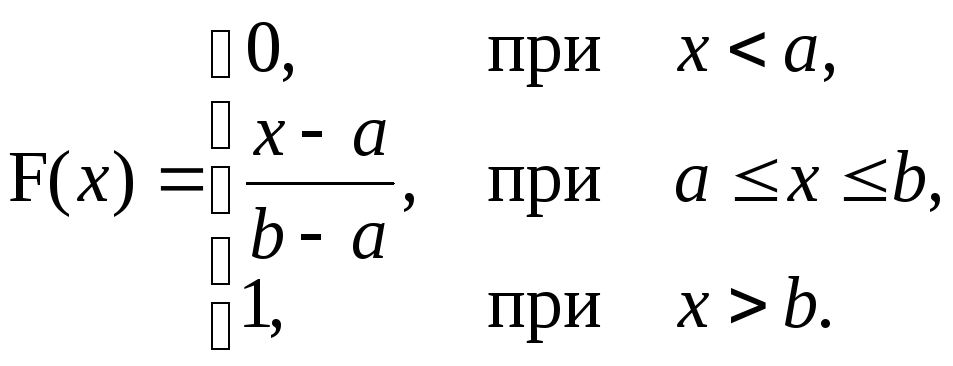

(7.2)

Вычислим основные числовые характеристики равномерного распределения. Математическое ожидание:

.

Таким образом, математическое ожидание случайной величины, распределенной равномерно на отрезке [a,b], совпадает с серединой этого отрезка.

Дисперсию находим по формуле

.

Так как рассматриваемое распределение симметрично относительно математического ожидания, то для него все центральные моменты, имеющие нечетный порядок, равны нулю. Следовательно, коэффициент асимметрии такого распределения равен нулю:

.

Вычислим теперь эксцесс равномерного распределения

.

Тогда

.

Вопрос: Что можно сказать о медиане и моде равномерного распределения?

7.2. Показательное распределение

Непрерывная случайная величина X называется распределенной по показательному (экспоненциальному) закону, если ее плотность распределения вероятностей задается формулой

(7.3)

Рис. 7.2

Показательное распределение часто встречается в теории массового обслуживания (например, X – время ожидания при техническом обслуживании или длительность телефонных разговоров, ежедневно регистрируемых на телефонной станции) и в теории надежности (например, X – срок службы радиоэлектронной аппаратуры).

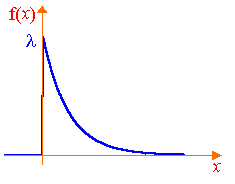
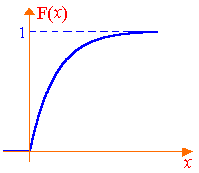
Найдем функцию распределения показательного распределения:

.

Итак

(7.4)

График плотности распределения и функции распределения для показательного распределения показаны на рис. 7.2.

Пусть T – непрерывная случайная величина, означающая длительность времени безотказной работы устройства. Функцией надежности R(t) называется функция, определяющая вероятность безотказной работы устройства в течение времени не меньшей t:

(7.5)

Поскольку F(t)=P(T<t), то

.

Если случайная величина имеет показательное распределение, то

(7.6)

где  – интенсивность отказов, т.е. среднее число отказов в единицу времени.

Показательное распределение обладает весьма важным свойством, характерным только для этого распределения: для любых чисел x₁ и x₂ выполняется равенство

(7.7)

Следствием этого свойства является т.н. свойство "отсутствия последействия", т.е. вероятность безотказной работы устройства на некотором интервале не зависит от времени предшествующей работы, а зависит только от его длительности.

Действительно, пусть A – безотказная работа на интервале (0,t₀), B – безотказная работа на интервале (t₀,t₀+t). Тогда AB – безотказная работа на интервале (0,t₀+t). Поскольку длительности времен безотказной работы для событий A, B и AB, соответственно, равны t₀, t, t₀+t, то

Найдем условную вероятность того, что устройство будет работать безотказно на интервале (t₀,t₀+t) при условии, что он уже пробовал безотказно в течение предшествующего интервала (0,t₀):

.

В результате получилось, что P(B)=P_A(B), т.е. в случае показательного закона вероятность безотказной работы устройства "в прошлом" не сказывается на величине вероятности его безотказной работы "в ближайшем будущем".

Например, при допущении метеориты распределены равномерно в пространстве и во времени, вероятность попадания метеорита в космический корабль не зависит от того, попали или нет в него метеориты до начала рассматриваемого интервала времени. Отсюда следует, что случайные моменты попадания метеоритов в космический корабль распределены по показательному закону.

Можно доказать и обратное утверждение: если случайная величина обладает свойством отсутствия последействия, то она обязана иметь показательное распределение. Таким образом, отсутствие последействия является характеристическим свойством показательного распределения.

Отметим, что показательное распределение тесно связано с распределением Пуассона, а именно: если времена между последовательными наступлениями некоторого события представляют собой независимые показательно распределенные (с одним и тем же параметром ) случайные величины, то число наступлений этого события за время t распределено по закону Пуассона с параметром t. Отметим также, что дискретным аналогом показательного распределения является геометрическое распределение.

Найдем числовые характеристики показательного распределения: математическое ожидание:

,

дисперсию:

,

среднее квадратичное отклонение:

.

Таким образом, для показательного распределения характерно, среднее квадратичное отклонение численно равно математическому ожиданию. Нетрудно убедится, что коэффициент асимметрии и эксцесс для показательного распределения являются постоянными величинами:

A = 2, E = 9.

Пример 7.1. Время распределения состава через горку –случайная величина, подчиненная показательному закону. Пусть =6 – среднее число поездов, которые горка может расформировать за 1 ч. Определить вероятность того, что время расформирования состава: а) меньше 30 мин; б) больше 10 мин, но меньше 40 мин.

Решение. а) Здесь нужно использовать функцию распределения показательного распределения F(t)=P(T<t)=1–e^–t. Вероятность того, что расформирование состава займет менее 30 мин = 0,5 ч есть

.

б) Здесь нужно использовать формулу

.

Вероятность того, что расформирование состава займет больше = 10 мин =1/6 ч, но меньше =40 мин = 2/3 ч, равно

Пример 7.2. Вероятность безотказной работы радиоэлемента распределена по показательному закону (t>0). найти вероятность того, что радиоэлемент проработает безотказно не менее 50 ч.

Решение. Используя функцию надежности R(t)=e^–t, получим