
- •ТЕМА 2.3. Частотно-избирательные свойства линейных систем и цепей. Электрические фильтры
- •Основные понятия о сложном сигнале. Частотная избирательность радиотехнических цепей
- •Комплексная частотная характеристика линейных цепей (систем)
- •Пусть на вход линейной цепи (рис. 11.4) подается синусоидальный сигнал
- •Линейные идеальные и реальные цепи
- •Логарифмические АЧХ (ЛАЧХ) и ФЧХ (ЛФЧХ)
- •Основные определения и классификация радиотехнических фильтров
- •Для полосового фильтра коэффициент прямоугольности равен отношению
- •Максимально-гладкая аппроксимация частотных характеристик фильтров
- •Для получения расчетных соотношений, позволяющих производить электрический расчет элементов фильтров, необходимо иметь аналитическое выражение, описывающее частотную характеристику фильтра, в частности АЧХ. Такoe выражение называют аппроксимирующим.
- •Безиндуктивные RC – фильтры
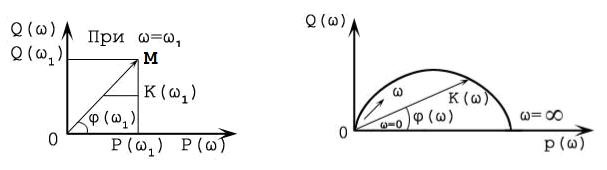
Рис. 11.7 |
Рис. 11.8 |
Таким образом, под АФК понимают кривую, которую описывает конец вектора комплексного коэффициента передачи цепи K( jω) на плоскости в прямоугольной системе координат Р(ω) – 0 - Q(ω).
Линейные идеальные и реальные цепи
Реальные сигналы являются колебаниями сложной формы и могут быть представлены в виде совокупности гармонических составляющих различных частот определяемой соотношением (11.1). Количество гармонических составлявших, их частоты и начальные фаза полностью определяются формой управлявшего сигнала, в котором заложена информация.
Сигнал, проходящий через линейную цепь, не будет искажен, если на выходе цепи сохраняется неизменным количество гармонических составляющих к их частот, а соотношения междуих амплитудами останутся такими же, как ж на входе цепи.
На форму сигнала, проходящего через цепь, влияет его запаздывание во времени на выходе цепи по отношению ко входу. Физически запаздывание объясняется тем, что в частотно-избирательных цепях, имеющих реактивные элементы L и С, время протекания электрических процессов конечно. Сигнал не будетискажен,есливсегармоническиесоставляющиенавыходецеписдвигаются по отношению к входу на одно и то же время.
Таким образом, электрическая цепь является неискажающей, если выполняются два условия:
•АЧХ цепи не зависит от частоты, т.е. K(ω) = const (рис. 11.9);
•все гармонические составляющие сигнала должны запаздывать на выходе цепи на одно и то же время, т.е. ФЧХ должна быть линейной
функцией |
частоты |
(рис.11.10): |
ϕ(ω) = −ω∆t3 ± nπ, |
|
|
где n = 0, ±1, ±2, ... ; |
∆t3 - время запаздывания |
|

Рис. 11.9 Рис. 11.10
Идеальной избирательной цепью называется цепь, которая не искажает сигнал с ограниченным спектром частот и не пропускает на выход сигналы, частотный диапазон которых лежит за пределами спектра полезного сигнала.
АЧХ идеальной избирательной цепи имеет прямоугольную (П - образную) форму, а ФЧХ является линейной функцией (рис. 11.11). Диапазон частот от ω1 до ω2 называется полосой пропускания идеальной избирательной цепи и
обозначается ∆ωπ .
Рис. 11.11 |
Рис. 11.12 |
Вреальных избирательных цепях технически реализовать идеальные АЧХ
иФЧХ практически невозможно (рис. 11.12). Однако при конструировании частотно-избирательных цепей стремятся приблизить АЧХ и ФЧХ к идеальным.
Логарифмические АЧХ (ЛАЧХ) и ФЧХ (ЛФЧХ)
При построении графиков АЧХ по оси ординат откладываются значения функции К(f). Однако диапазон изменения К(f) может быть значительным, что не только создает неудобства в графическом построении. АЧХ (за счет большой протяженности графика по оси ординат), но и снижает ценность его использования при анализе АЧХ на отдельных участках (рис. 11.13, а).
В целях устранения указанных недостатков при построении графиков АЧХ значения функции К(f) = Xm / Sm откладывают в логарифмическом масштабе:
N(Б) = lg K( f ) = lg Xm ,
Sm
где N (Б) - логарифмическая единица, получившая название бел (Б).
Однако на практике получила широкое применение другая логарифмическая единица, названная децибелом (дБ) (см. рис. 11.13, б). Причем, если Xm и Sm имеют смысл мощности, тогда децибел определяется как

N, дБ =10lg X m .
Sm
Так как мощность пропорциональна квадрату напряжения или тока, то логарифмические единицы в применении к этим электрическим величинам
запишутсяввиде N,дБ = 20lg Xm гдеХm, Sm имеютсмыслнапряженияилитока.
Sm
Если при построении графика АЧХ по оси абсцисс откладывать непосредственно значения частоты (см. рис. 11.13, а, б), то такой график будет иметь те же недостатки (по оси абсцисс), которые были указаны при построении масштаба по оси ординат. Поэтому при графическом построении АЧХ по оси абсцисс откладывают часто не абсолютные значения частоты f, а десятичный логарифм (см. рис. 11.13, в).
Логарифмической фазо-частотной характеристикой (ЛФЧХ) называют ФЧХ φ(ω), построенную в логарифмическом масштабе частот.
Основные определения и классификация радиотехнических фильтров
Радиотехническим фильтром, называется устройство, обладающее частотной избирательностью и предназначенное для селекции электрических колебаний в заданной полосе частот. Область частот, в которой фильтр пропускает колебания с небольшим затуханием, называется полосой пропускания фильтра или полосой прозрачности.
Фильтры могут быть классифицированы по различным признакам, например:
•по типам схем;
•по типам используемых элементов;
•по пропускным частотам.
Классификация фильтров по типам схем.
Взависимости от конструкции цепи различают следующие типы фильтров:
•Г-образный (рис. 11.14);
•Т-образные (рис. 11.15);

•П-образные (рис. 11.16);
•Лестничные фильтры, состоящие из элементарных Г-, Т- и П- образных фильтров (рис. 11.17);
•Мостовые фильтры (рис. 11.18);
Классификация Фильтров по типам элементов.
В зависимости от вида применяемых элементов различают следующие типы фильров:
•LС (реактивные) фильтры;
•RC (без индуктивные) фильтры;

•Электромеханические фильтры, в которых применяются пьезоэлектрические и магнитнострикционные резонаторы.
Классификация фильтров по пропускаемым частотам.
Взависимостиотназначенияиместоположенияполосыпропусканиянаоси частот различают следующие вида фильтров.
Фильтры нижних частот (ФНЧ) пропускают колебания с частотами ниже заданной частоты, называемой частотой среза, и подавляют колебания других, более высоких частот. На рис. 11.19 приведены нормированные АЧХ для идеального и реального ФНЧ;
KH (ω) = |
K(ω) |
= |
K(ω) |
. |
|
|
|||
|
Kmax |
K(0) |
||
На рис. 11.20 приведены примеры схем ФНЧ.
Основнойколичественнойхарактеристикойфильтраявляетсякоэффициент прямоугольности
Kn = ∆ω0.1 , ∆ω0.7
равный отношению полос пропускания на уровне 0.1 и 0.7 соответственно. Для идеального ФНЧ Kn = 1, для реального ФНЧ – Kn > 1.
Фильтры высоких частот (ФВЧ), пропускают колебания на частотах выше заданной ωси подавляют колебания более низких частот. Нарис. 11.22 – примеры схем ФВЧ. Коэффициент прямоугольности ФВЧ равен отношению частот среза
ωс и ω0.1:
Kn = ωc .
ω0.1
