
LR_TsOS_1_LDS
.pdf
Федеральное агентство связи ордена Трудового Красного Знамени
федеральное государственное бюджетное образовательное учреждение высшего образования
«Московский технический университет связи и информатики»
Кафедра радиотехнических систем
Практикум по дисциплине
ЦИФРОВАЯ ОБРАБОТКА СИГНАЛОВ
Лабораторная работа № 2
ИССЛЕДОВАНИЕ ХАРАКТЕРИСТИК ЛИНЕЙНЫХ ДИСКРЕТНЫХ СИСТЕМ
Москва, 2016 г
УДК 621.391:519.27 |
План подготовки УМД 2016/2017 уч. года |
Практикум по дисциплине
«ЦИФРОВАЯ ОБРАБОТКА СИГНАЛОВ»
ИССЛЕДОВАНИЕ ХАРАКТЕРИСТИК ЛИНЕЙНЫХ ДИСКРЕТНЫХ СИСТЕМ
В лабораторной работе № 2 производится моделирование линейных дискретных систем, вычисляются импульсные и передаточные, амплитудно-частотные и фазочастотные характеристики рекурсивных звеньев 2-го порядка.
Основной применяемый метод экспериментального исследования – имитационное моделирование на персональной ЭВМ с применением среды имитационного моделирования радиотехнических систем «Спектр-2».
Для студентов радиотехнических и телекоммуникационных специальностей.
Список лит. 3 назв., ил. 19, табл. 5.
Составители: Лобов Е.М., Смердова Е.О. Рецензент:
Издание утверждено советом факультета Радио и Телевидения. Протокол № … от
_._.2016 г.
2
ЛАБОРАТОРНАЯ РАБОТА № 2
ИССЛЕДОВАНИЕ ХАРАКТЕРИСТИК ЛИНЕЙНЫХ ДИСКРЕТНЫХ СИСТЕМ
Цель работы:
Изучить математическое описание линейных дискретных систем (ЛДС) и овладеть программными средствами их моделирования и анализа в среде «Спектр-2»
Номер варианта выбирается студентом из следующей таблицы:
Таблица 1. Исходные данные
Переменная |
Назначение |
Значение |
||
|
|
|
|
|
Nбр |
Номер бригады |
|
Nбр |
|
b0 |
Коэффициенты |
числителя |
b0 0,5 0, 02Nбр |
|
|
|
|||
b1 |
передаточной функции |
b1 b0 ( 1)Nбр 1(0,9822 0, 0178Nбр ) |
||
b2 |
|
|
b2 b0 0,8 0, 2(Nбр mod 5) |
|
|
|
|
|
|
a0 |
Коэффициенты |
знаменателя |
a0 1 |
|
a1 |
передаточной функции |
a1 ( 1)Nбр (0, 7778 0, 025Nбр ) |
||
a2 |
|
|
a2 0, 64 0, 006Nбр |
|
|
|
|
|
|
|
|
|
|
|
N1 |
Длина ИХ |
|
10 |
|
|
|
|
|
|
N2 |
Длина воздействия |
4 |
|
|
|
|
|
|
|
fд |
Частота дискретизации |
fд 1000Nбр |
|
|
|
|
|||
|
|
|
|
|
Nбр 1, 2,..., 40
3
1 Домашний расчёт.
1.1 Домашний расчёт состоит из следующих пунктов:
1.Формирование основных характеристик линейной дискретной системы.
2.Определение устойчивости линейной дискретной системы.
3.Вычисление импульсной характеристики по разностному уравнению.
4.Вычисление импульсной характеристики по общей формуле.
5.Вычисление реакции линейной дискретной системы по формуле свёртки.
6.Вычисление реакции линейной дискретной системы по разностному уравнению.
7.Экспресс-анализ АЧХ и ФЧХ.
Пример расчёта домашнего задания.
1.2 Формирование основных характеристик линейной дискретной системы второго порядка.
Зададим линейную дискретную систему (ЛДС) её передаточной (системной) функцией H (z) и разностным уравнением с коэффициентами:
b0 1, b1 0.7 , b2 0.49 , a1 0.7 , a2 0.49 .
Общий вид разностного уравнения (1) и передаточной (системной) функции (2):
|
|
M |
|
|
|
|
|
N |
|
|
|
|
|
y(n) bk x(n k) ak y(n k) . |
(1) |
||||||||||||
|
|
k 0 |
|
|
|
|
|
k 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
M |
|
|
|
|
|
|
|
|
Y (z) |
|
|
|
|
bk z k |
|
|
|
|
|
|
H (z) |
|
|
|
k 0 |
|
|
|
(2) |
||||
|
|
|
|
|
|
|
|||||||
|
X (z) |
|
|
N |
|
|
|
||||||
|
|
|
|
|
1 ak z k |
|
|
|
|
||||
|
|
|
|
|
|
|
|
k 1 |
|
|
|
|
|
Порядок ЛДС определяется наибольшим из значений M и N , в нашем |
|||||||||||||
случае M N 2 (ЛДС второго |
порядка). Тогда |
|
разностное уравнение |
и |
|||||||||
передаточная функция будут выглядеть следующим образом: |
|
||||||||||||
y(n) b0 x(n) b1x(n 1) b2 x(n 2) a1 y(n 1) a2 y(n 2) |
(3) |
||||||||||||
x(n) 0.7x(n 1) 0.49x(n 2) 0.7 y(n 1) 0.49 y(n 2) |
|
||||||||||||
H (z) |
b |
b z 1 |
b z 2 |
|
1 0.7z 1 |
0.49z 2 |
|
||||||
0 |
1 |
2 |
|
|
|
|
|
|
(4) |
||||
1 a z 1 a z 2 |
1 0.7z 1 |
0.49z 2 |
|||||||||||
|
|
|
|
||||||||||
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
На этом будем считать ЛДС заданной.
4

1.3 Определение устойчивости ЛДС.
ЛДС считается устойчивой, если ограниченное по амплитуде воздействие на входе системы порождает ограниченную по амплитуде реакцию системы на выходе.
Одним из критериев устойчивости является нахождение полюсов передаточной (системной) функции внутри единичной окружности с центром в начале координат z -плоскости.
Полюсы - это корни полинома знаменателя системной функции. Для их нахождения нужно приравнять знаменатель передаточной (системной) функции к нулю и решить получившееся уравнение.
Умножим числитель и знаменатель (4) на z2 и получим H (z) в дробнорациональной форме (в форме отношения полиномов от z):
|
|
|
|
|
|
|
|
|
|
|
|
|
|
H (z) |
z2 0.7z 0.49 |
|
|
|
(5) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z2 0.7z 0.49 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Приравняем к нулю полином знаменателя: |
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z2 0.7z 0.49 0 , |
|
|
(6) |
|||||||
и найдем его корни: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
z |
|
|
0.7 |
|
|
0.72 4 * 0.49 *1 |
|
|
0.7 |
|
1.47 |
|
0.35 j1.2124 |
0.35 j0.6062 , |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
1,2 |
|
|
|
|
|
|
|
|
|
|
|
2 *1 |
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(7) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
где |
|
j |
1 - |
мнимая единица. Полюсы передаточной функции (4) |
равны |
||||||||||||||||||||||
z |
0.35 j0.6062 , |
причем |
z |
z* , |
где звездочка сверху означает операцию |
||||||||||||||||||||||
1,2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
комплексного |
|
сопряжения. |
|
|
Модуль |
полюсов |
равен |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
r |
|
z |
|
|
|
|
z* |
|
|
0.352 |
0.60622 |
|
0.7 . |
То есть |
мы |
имеем два комплексно- |
|||||||||||
|
|
|
|
|
|
||||||||||||||||||||||
|
|
||||||||||||||||||||||||||
|
|
1 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
сопряжённых полюса по модулю меньших единицы, – следовательно, ЛДС устойчива. Полюса ЛДС могут быть записаны в показательной форме как
z re j , r |
|
|
arctg |
|
0.6062 |
|
1.0472 |
|
|
0.352 0.60622 |
0.7 , |
. (8) |
|||||||
|
|
|
|||||||
1,2 |
|
|
|
|
|
|
|||
|
|
|
|
0.35 |
|
|
|
||
|
|
|
|
|
|
Нули ЛДС (корни числителя передаточной функции) находятся аналогичным образом, приравнивая к нулю числитель дробно-рациональной функции (5). Нули ЛДС равны
z |
0.7 |
0.72 4 * 0.49 *1 |
|
0.7 |
|
1.47 |
|
0.35 j1.2124 |
0.35 |
j0.6062 |
|
|
|
|
|
|
|||||
01,2 |
|
2 *1 |
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
(9) |
Запишем нули в показательной форме:
5
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.6062 |
|
|
|
|
|
j |
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|||
z |
01,2 |
r e 0 |
, r |
0.35 |
|
0.6062 |
|
0.7 |
, |
|
0 |
arctg |
|
|
|
2.0944 |
. (10) |
|
|
|
|||||||||||||||
|
0 |
0 |
|
|
|
|
|
|
|
|
0.35 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
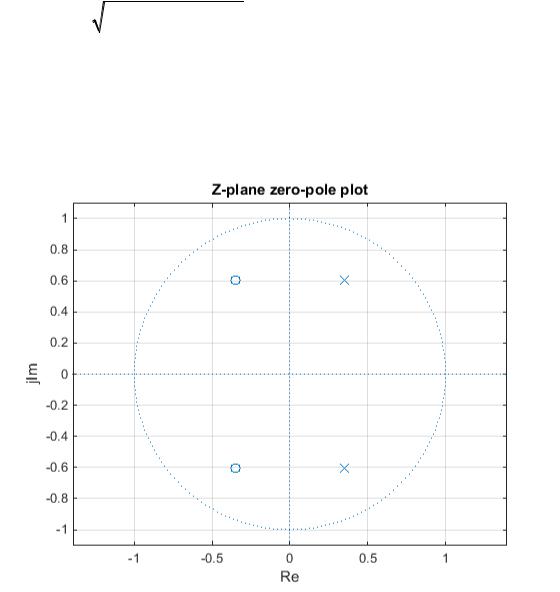
Нуль-полюсная диаграмма представлена ниже на рисунке 1. Крестиками на диаграмме отмечены полюса, а кружочками – нули ЛДС. Как видно из диаграммы, полюса лежат внутри единичной окружности с центром в начале координат. ЛДС устойчива. Положение нулей на устойчивость ЛДС не влияет.
Рисунок 1. Нуль-полюсная диаграмма
1.4 Вычисление импульсной характеристики по разностному уравнению.
Для примера возьмём длину импульсной характеристики (ИХ) равную десяти отсчётам ( n 0,1,2,...,9 в (1)).
Как известно, импульсная характеристика – это реакция ЛДС на цифровой единичный импульс при нулевых начальных условиях. Поэтому для определения ИХ по разностному уравнению требуется принять за входной сигнал воздействие вида:
|
|
|
1, n 0 |
|
|
x(n) (n) |
, |
(11) |
0,иначе |
|
|
т.е. входной сигнал не равен нулю только при x(n) x(0) 1.
6

Перейдём к определению отсчётов ИХ по формуле (3). При этом последовательность на выходе ЛДС будет являться ее импульсной характеристикой h(n) y(n) .
Положим n 0
h(0) b0 x(0) b1x( 1) b2 x( 2) a1h( 1) a2h( 2) b0 x(0) 1 1 1 Отсчёты входного сигнала x( 1) x( 2) 0 по форме воздействия (см.(11)), а отсчёты
реакции ЛДС h( 1) и h( 2) равны нулю исходя из нулевых начальных условий1 и физической реализуемости ЛДС. Далее отсчёты воздействия и ИХ, равные нулю из этих соображений, будут опускаться.
Продолжим расчёт. n 1
h(1) b1x(0) a1h(0) 0.7 1 0.7 1 1.4 n 2
h(2) b2 x(0) a1h(1) a2h(0) 0.49 0.7 1.4 0.49 0.98 n 3
h(3) a1h(2) a2h(1) 0.7 0.98 0.49 1.4 0
Начиная с h(3) и далее все отсчёты воздействия будут равны нулю, поэтому реакция будет определяться только предыдущими своими отсчётами, умноженными на соответствующие им коэффициенты a1 и a2 . Поэтому дальнейшие вычисления производятся по сокращённой формуле:
h(n) a1h(n 1) a2h(n 2) |
(12) |
Подставляя в (12) значения отсчётов ИХ и коэффициентов a1 и a2 вычислим
оставшиеся 6 отсчётов: n 4
h(4) a1h(3) a2h(2) 0.4802 n 5
h(5) a1h(4) a2h(3) 0.3361 n 6
h(6) a1h(5) a2h(4) 0 n 7
h(7) a1h(6) a2h(5) 0.1647 n 8
h(8) a1h(7) a2h(6) 0.1153
1 Входные и выходные отсчеты с формально отрицательными значениями индекса физически хранятся в элементах памяти ЛДС. Нулевые начальные условия требуют, чтобы в начальный момент времени все элементы памяти были сброшены в нулевое состояние (хранение нулей).
7

n 9
h(9) a1h(8) a2h(7) 0
Десять отсчётов импульсной характеристики по разностному уравнению найдены.
1.5Пример расчёта домашнего задания. Вычисление импульсной характеристики по общей формуле для рекурсивного звена 2-го порядка с учетом нулевых начальных условий (ННУ).
Вычислим импульсную характеристику для ЛДС второго порядка по общей формуле, полученной из передаточной функции с помощью обратного z - преобразования:
|
b rn |
sin (n 1) |
|
, n 0 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
0 |
|
sin() |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
sin (n 1) |
|
|
|
|
|
|
|
|
|
|
||
h(n) |
b rn |
|
b rn 1 |
sin(n ) |
, n 1 |
|
|
, (13) |
||||||||
|
|
|
|
|
||||||||||||
|
|
0 |
|
sin() |
1 |
sin() |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
sin (n 1) |
|
|
|
|
|
|
sin (n 1) |
|
|
|||
|
|
|
|
|
|
b rn 1 |
sin(n ) |
b rn 2 |
|
, n 2 |
||||||
|
b rn |
|
|
|||||||||||||
|
|
|
|
|
||||||||||||
|
|
0 |
|
sin() |
1 |
sin() |
2 |
|
sin() |
|
||||||
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
где r 0.7 |
|
0.352 0.60622 |
- модуль полюсов (корней |
знаменателя) |
||||||||||||
|
|
|
|
|
|
|
|
|
|
0.6062 |
|
|
|
|||
передаточной |
|
|
функции, arctg |
|
|
1.0472 |
- положительный |
|||||||||
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
0.35 |
|
|
|
|
|
|
аргумент одного из полюсов передаточной функции (см. (8) и пункт 1.3). Также, как и в предыдущем задании вычисляем десять отсчётов ИХ начиная с нулевого:
h(0) b r0 |
|
sin( ) |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
0 |
|
|
|
sin( ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
h(1) b r |
sin 2 |
|
b 1.4 |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
0 |
sin( ) |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
h(2) b r2 |
sin 3 |
|
|
b r |
sin(2 ) |
|
b |
0.98 |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||
0 |
|
|
|
|
sin( ) |
|
|
|
|
1 |
sin( ) |
|
|
2 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
h(3) b r3 |
sin 4 |
|
|
b r2 |
sin(3 ) |
|
b r |
sin 2 |
|
0 |
|||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||
0 |
|
|
|
|
sin( ) |
|
|
|
|
1 |
|
|
sin( ) |
|
|
|
2 |
sin( ) |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
h(4) b r4 |
sin 5 |
|
b r3 |
sin(4 ) |
b r2 |
sin 3 |
0.4802 |
||||||||||||||||||
|
|
|
|||||||||||||||||||||||
0 |
|
|
|
|
sin( ) |
1 |
|
|
sin( ) |
|
|
|
2 |
|
sin( ) |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
h(5) b r5 |
sin 6 |
|
|
b r4 |
|
sin(5 ) |
|
|
|
b r3 |
sin 4 |
|
|
|
0.3361 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
0 |
|
|
|
sin( ) |
1 |
|
|
|
|
sin( ) |
2 |
|
|
|
|
sin( ) |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
h(6) b r6 |
|
sin 7 |
b r5 |
sin(6 ) |
|
b r4 |
sin 5 |
|
0 |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
0 |
|
|
|
sin( ) |
1 |
|
|
|
|
sin( ) |
2 |
|
|
|
|
sin( ) |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
h(7) b r7 |
sin 8 |
|
b r6 |
sin(7 ) |
b r5 |
sin 6 |
0.1647 |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
0 |
|
|
|
sin( ) |
1 |
|
|
|
|
sin( ) |
2 |
|
|
|
|
sin( ) |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
h(8) b r8 |
sin 9 |
|
b r7 |
sin(8 ) |
|
b r6 |
sin 7 |
|
0.1153 |
||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||
0 |
|
|
|
sin( ) |
1 |
|
|
|
|
sin( ) |
2 |
|
|
|
|
sin( ) |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
sin 10 |
|
|
|
|
|
|
|
sin(9 ) |
|
|
|
|
|
|
sin 8 |
|
|
|||||||||||
h(9) b r9 |
|
|
|
b r8 |
b r7 |
|
|
0 |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
0 |
|
|
|
sin( ) |
|
|
1 |
|
|
|
|
sin( ) |
2 |
|
|
|
|
|
sin( ) |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Как видно из расчёта, отсчёты ИХ, рассчитанные двумя методами, совпадают.
1.6Вычисление реакции ЛДС по формуле свёртки.
Вкачестве воздействия x(n) примем прямоугольный импульс длины
N x 4 : |
|
|
|
|
x |
1 |
|
1,0 n N |
|
|
|
x(n) |
|
|
(14) |
0,иначе |
|
|
|
Формула свёртки, по которой будет определяться реакция ЛДС, |
|||
представляет собой следующее выражение: |
|
|
|
n |
|
|
|
y(n) h(k)x(n k) |
(15) |
||
k 0 |
|
|
|
Общая длина выходного сигнала дискретной системы определяется |
|||
как: |
|
|
|
N y N Nx 1 , |
(16) |
||
где N - длина импульсной характеристики системы h(n) , Nx |
-длина входного |
||
сигнала x(n) . |
|
|
|
В рассматриваемом примере N y 10 4 1 13 отсчётов выходного
сигнала.
После определения длины последовательности выходного сигнала y(n) необходимо рассчитать его отсчёты по формуле свёртки (см. (15)) следующим образом:
положим n 0
9
n 0
y(0) h(k)x(n k) h(0)x(n) h(0)x(0) 11 1
k 0
n 1
n 1
y(1) h(k)x(n k) h(0)x(n) h(1)x(n 1) h(0)x(1) h(1)x(0) 2.4
k 0
n 2
n 2
y(2) h(k)x(n k) h(0)x(n) h(1)x(n 1) h(2)x(n 2)
k0
h(0)x(2) h(1)x(1) h(2)x(0) 3.38
n 3
n 3
y(3) h(k)x(n k) h(0)x(n) h(1)x(n 1) h(2)x(n 2) h(3)x(n 3)
k 0
h(0)x(3) h(1)x(2) h(2)x(1)
n 4
n 4
y(4) h(k)x(n k) h(0)x(4)
k 0
h(3)x(0) 3.38
h(1)x(3) h(2)x(2) h(3)x(1) h(4)x(0) 1.8998
Здесь умножение h(0)x(4) 0 из-за равенства нулю пятого отсчёта воздействия x(4) 0 (см. (14)). Далее расчётные формулы будут приведены
без равных нулю множителей. n 5
n 5
y(5) h(k)x(n k) h(2)x(3) h(3)x(2) h(4)x(1) h(5)x(0) 0.1637
k 0
n 6
n 6
y(6) h(k)x(n k) h(3)x(3) h(4)x(2) h(5)x(1) h(6)x(0) 0.8163
k 0
n 7
n 7
y(7) h(k)x(n k) h(4)x(3) h(5)x(2) h(6)x(1) h(7)x(0) 0.6516 .
k 0
Продолжая считать таким же образом и учитывая, что, начиная с 11 отсчёта, ИХ полагается равной нулю, получим следующие значения оставшихся пяти отсчётов реакции ЛДС на прямоугольный единичный импульс:
y(8) 0.0561 y(9) 0.28
10
