
LR_TsOS_4_BIKh_IKh
.pdf
Федеральное агентство связи
ордена Трудового Красного Знамени
федеральное государственное бюджетное образовательное учреждение высшего образования
«Московский Технический Университет Связи и Информатики»
Кафедра радиотехнических систем
Практикум по дисциплине
ЦИФРОВАЯ ОБРАБОТКА СИГНАЛОВ
Лабораторная работа № 5
СИНТЕЗ ЦИФРОВЫХ БИХ-ФИЛЬТРОВ МЕТОДОМ ИНВАРИАНТНОСТИ ИМПУЛЬСНОЙ ХАРАКТЕРИСТИКИ
Москва, 2019 г.
УДК 621.391:519.27
Практикум
по дисциплине
«ЦИФРОВАЯ ОБРАБОТКА СИГНАЛОВ»
СИНТЕЗ ЦИФРОВЫХ БИХ-ФИЛЬТРОВ
МЕТОДОМ ИНВАРИАНТНОСТИ ИМПУЛЬСНОЙ ХАРАКТЕРИСТИКИ
В лабораторной работе № 5 изучается метод инвариантности импульсной характеристики на примере синтеза цифрового ФНЧ по аналоговым фильтрам прототипам Чебышёва и Баттерворта. Проводится моделирование синтезированного цифрового фильтра в среде «Спектр-2».
Для студентов радиотехнических и телекоммуникационных направлений.
Список лит. 3 назв., ил. 6, табл. 5.
Составители: доц. Лобов Е.М., Лобова Е.О.
Рецензент
2
ЛАБОРАТОРНАЯ РАБОТА № 5
СИНТЕЗ ЦИФРОВЫХ БИХ-ФИЛЬТРОВ МЕТОДОМ ИНВАРИАНТНОСТИ ИМПУЛЬСНОЙ ХАРАКТЕРИСТИКИ
Цель работы: Изучение синтеза цифровых БИХ-фильтров методом инвариантности импульсной характеристики на примере синтеза цифрового ФНЧ по аналоговым фильтрам прототипам Чебышёва и Баттерворта. Проведение моделирования синтезированного цифрового фильтра проводится в среде «Спектр-2».
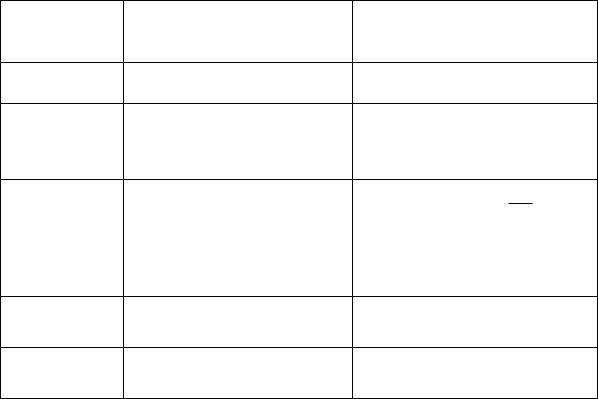
Номер варианта выбирается студентом из следующей таблицы:
Условные
обозначения
Fд
F1
Fз
a |
р max |
|
a р min
Список требований |
Задаваемые значения |
|
Частота дискретизации |
F 10000 200N |
бр |
д |
||
Граничная частота ПП
Граничная частота ПЗ
Максимально допустимое затухание в ПП (дБ)
Минимально допустимое затухание в ПЗ (дБ)
F 1200 20N |
бр |
– Баттерворт |
||||||
1 |
|
|
|
|
|
|
||
F 1500 30N |
бр |
– Чебышев |
||||||
1 |
|
|
|
|
|
|
||
F 3120 50N |
|
10 |
N |
бр |
|
– |
||
бр |
|
|
|
|
||||
з |
|
|
5 |
|
||||
|
|
|
|
|
|
|
||
Баттерворт |
|
|
|
|
|
|
|
|
F 2800 40N |
бр |
– Чебышев |
||||||
з |
|
|
|
|
|
|
|
|
a |
р max |
0.4455 |
|
|
|
a |
р min |
40 |
|
|
N |
b |
1, 2,...30 |
|
|
Тип функции фильтрации определяется по чётности/нечётности последней цифры в номере студенческого билета. Если последняя цифра номера нечётная, то требуется провести синтез фильтра Чебышёва, если чётная, то рассчитывается фильтр Баттерворта. Все рассматриваемые фильтры являются фильтрами нижних частот.
3

1 Домашний расчёт
1.1Домашний расчёт состоит из следующих пунктов:
1.Формулировка требований к ЦФ.
2.Запись аналитического выражения передаточной функции АФП ФНЧ (передаточная функция АФП ФНЧ берётся из лабораторной работы «Синтез цифровых БИХ-фильтров методом билинейного z - преобразования»).
3.Переход от передаточной функции АФП к передаточной функции ЦФ с помощью метода инвариантности импульсной характеристики.
4.Запись аналитического выражения передаточной функции ЦФ в виде суммы передаточных функций биквадратных звеньев.
1.2Пример расчёта домашнего задания для ФНЧ Баттерворта
Спроектируем ФНЧ Баттерворта. Сформулируем требования к фильтру, - для ФНЧ это:
1. |
значения граничных частот полосы задержания и полосы пропускания |
F |
и |
|
( |
3 |
|||
соответственно); |
|
|
|
|
2. |
значение коэффициента максимального ослабления в полосе пропускания aр max |
, дБ; |
||
3. |
значение коэффициента минимального ослабления в полосе задержания aр min |
, дБ; |
|
|
F1
4. частота дискретизации сигналов, обрабатываемых фильтром, |
F |
|
|
д |
|
Примем значения граничных частот и коэффициентов aр max |
, |
|
аналогового фильтра прототипа (АФП) равными: |
|
|
.
a |
р min |
|
низкочастотного
F1 1900 Гц, F3 |
4940 |
Гц, |
Fд 17000 Гц , |
|
|
aр max 0.4455 , |
aр min 40 |
|
|
|
|
|
F |
|
|
Проведём нормировку частоты дискретизации |
Fд |
: Fs |
|
д |
1.424 |
|
2 F |
||||||
|
|
|
|
|
||
|
|
|
|
1 |
|
нормированное значение периода дискретизации T 1 / Fs 0.7022 .
ивычислим
В лабораторной работе «Синтез цифровых БИХ-фильтров методом билинейного z - преобразования» в соответствии с вариантом была получена операторная передаточная функция АФП нижних частот шестого порядка N 6 , записывающаяся в общем виде как
|
|
|
Н ( p) |
k |
, |
(1.1) |
|
|
|
|
|
||||
|
|
|
( p p1 )( p p2 )( p p3 )( p p4 )( p p5 )( p p6 ) |
||||
где k |
1 |
|
- коэффициент усиления, - коэффициент неравномерности |
рабочего |
|||
|
|||||||
|
|
|
|
|
|||
ослабления, |
pi , i 1 6 - комплексные полюса передаточной функции. |
|
|
||||
Рассчитаем передаточную характеристику для цифрового фильтра (ЦФ) методом инвариантности импульсной характеристики (метод инвариантности ИХ).
4

Для примера возьмём операторную передаточную функцию фильтра Баттерворта нижних
частот из домашнего |
расчёта лабораторной работы «Синтез цифровых БИХ-фильтров |
методом билинейного |
z - преобразования». |
Полюсы передаточной функции в этом случае равны
а коэффициент усиления равен
p |
0.31235 j1.1657 |
|
|
1 |
|
|
|
p |
0.31235 j1.1657 |
|
|
2 |
|
|
|
p |
0.85335 j0.85335 |
|
|
3 |
|
, |
|
p |
0.85335 j0.85335 |
||
|
|||
4 |
|
|
|
p |
1.1657 j0.31235 |
|
|
5 |
|
|
|
p |
1.1657 j0.31235 |
|
|
6 |
|
|
|
k 3.0893. |
|
||
(1.2)
Разложим операторную передаточную функцию (1.1) дробь на простые дроби.
Н ( p) |
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( p p )( p p )( p p )( p p |
)( p p )( p p ) |
||||||||
1 |
|
2 |
|
3 |
|
4 |
5 |
|
6 |
|
|
A |
|
A |
|
|
A |
|
A |
|
1 |
2 |
|
3 |
4 |
||||
|
|
|
|
|
|
||||
|
|
( p p ) |
|
( p p |
) |
( p p ) |
|
( p p |
|
|
|
1 |
|
2 |
|
|
3 |
|
4 |
представляющую собой правильную
|
|
|
|
|
|
|
A |
|
A |
|
|
|
5 |
|
6 |
, |
(1.3) |
|
|
||||
) |
( p p ) |
|
( p p |
) |
|
|
5 |
|
6 |
|
|
где Ai , |
i 1 6 - |
коэффициенты разложения на простые дроби, |
которые определяются |
|||||||||||||||||||||
согласно следующему правилу |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
A lim |
p p |
H |
p , |
i 1 6 |
. |
|
|
|
|
|
|
|
(1.4) |
||||||
|
|
|
|
|
i |
p p |
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Используя правило (1.4) и выражение (1.1) определим значения коэффициентов |
Ai , |
i 1 6 |
||||||||||||||||||||||
в общем виде |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
A1 lim p p1 H p lim |
p p1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
p |
p1 |
|
|
p p1 |
|
|
( p p1 )( p p2 )( p p3 )( p p4 )( p p5 )( p p6 ) |
|
||||||||||||||||
lim |
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
( p p )( p p )( p p )( p p )( p p ) |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
1 |
|
( p p )( p p )( p p )( p p )( p p ) |
||||||||||||||||||||||
p p |
|
|
2 |
3 |
4 |
5 |
|
|
6 |
|
|
|
1 |
2 |
1 |
|
3 |
1 |
4 |
1 |
5 |
1 |
|
6 |
|
|
|
|
|
|
|
|
|||||||||||||||||
0.2495 j0.4321 ;
аналогично
A lim |
p p |
H p |
|
|
|
|
|
k |
|
|
|
0.2495 |
||
|
|
|
|
|
|
|
|
|
||||||
2 |
2 |
|
2 |
|
( p |
p )( p |
p )( p |
p )( p |
p )( p |
p ) |
||||
|
p p |
|
|
|
2 |
1 |
2 |
3 |
2 |
4 |
2 |
5 |
2 |
6 |
|
|
|
|
|
||||||||||
j
0.4321
;
A lim |
p p |
H p |
|
|
|
|
|
k |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|||||
3 |
3 |
|
2 |
|
( p |
p )( p |
p )( p |
p )( p p )( p p ) |
||||||
|
p p |
|
|
|
3 |
1 |
3 |
2 |
3 |
4 |
3 |
5 |
3 |
6 |
|
|
|
|
|
||||||||||
1.8622
;
4 |
p p |
|
4 |
|
|
|
|
|
|
|
k |
1.8622 ; |
A |
lim |
|
p p |
H |
|
p |
|
|
( p4 |
p1 )( p4 |
p2 )( p4 p3 )( p4 p5 )( p4 p6 ) |
|
|
4 |
|
|
|
|
|
|
|
|
5

A lim |
p p |
H p |
|
|
|
|
|
k |
|
|
|
1.6127 |
||
|
|
|
|
|
|
|
|
|
||||||
5 |
5 |
|
5 |
|
( p |
p )( p |
p )( p |
p )( p |
p )( p |
p ) |
||||
|
p p |
|
|
|
5 |
1 |
5 |
2 |
5 |
3 |
5 |
4 |
5 |
6 |
|
|
|
|
|
||||||||||
j2.7933
;
A lim |
p p |
H p |
|
|
|
|
|
k |
|
|
|
1.6127 |
||
|
|
|
|
|
|
|
|
|
||||||
6 |
6 |
|
6 |
|
( p |
p )( p |
p )( p |
p )( p |
p )( p |
p ) |
||||
|
p p |
|
|
|
6 |
1 |
6 |
2 |
6 |
3 |
6 |
4 |
6 |
5 |
|
|
|
|
|
||||||||||
j2.7933
.
Из расчёта видно, что четыре из шести коэффициентов
Ai
,
i
1 6
являются комплексными
и попарно комплексно сопряжены:
A1
и
A2
,
A5
и
A6
. Обозначим для удобства
A2
A* 1
,
A6 A5* . Коэффициенты
нулю) и равными |
A3 |
|
A3 и A4 являются вещественными (то есть мнимая часть равна
A4 |
. Можно представить коэффициенты |
Ai |
как |
Ai |
ci |
jdi |
, |
A* c |
jd |
i |
i 1 3 , где |
c |
и d |
i |
- вещественная и |
|
i i |
|
|
i |
|
|
|
||
соответственно. Полагается, что коэффициент |
Ai ci |
|||||||
мнимая часть коэффициента
jdi |
вычислен для полюса |
pi |
Ai
из
второго квадранта (т.е. с отрицательной вещественной частью и положительной мнимой частью).
Передаточная функция цифрового фильтра синтезированного по методу инвариантности ИХ определяется как
H N - порядок фильтра, в данном случае
Удобно представить формулу (1.5) как объединить попарно слагаемые,
N |
A |
|
|
|
|
|
z |
|
|
|
|
||
|
i |
|
|
, |
(1.5) |
|
1 e |
p T |
z |
1 |
|||
i 1 |
i |
|
|
|
||
|
|
|
|
|
||
|
|
|
|
|
|
|
N 6 . |
|
|
|
|
|
|
сумму биквадратных звеньев. Для этого необходимо имеющие комплексно сопряжённые значения
коэффициентов
Ai
,
i 1 6
и
e |
p T |
|
i |
||
|
.
Для
A1
и
A* 1
вещественная часть равна
c1
0.2495
, мнимая
d1
0.4321
;
Коэффициенты
A3
и
A4
,
A |
A |
3 |
4 |
является вещественными, поэтому
c2
1.8622
, а
d |
2 |
|
0
;
Для
A5
и
A* 5
вещественная часть равна
c3
1.6127
, мнимая
d |
3 |
|
2.7933
;
Экспонента в формуле (1.5) может быть представлена в общем виде как
|
|
e piT e i j i T |
e iT e j iT |
e iT cos iT je T |
sin iT i j i , |
|
(1.6) |
|||||||||||||||
где |
i и i - вещественная и мнимая (без учёта знака) часть e |
p T |
соответственно. |
|
||||||||||||||||||
i |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Полюса можно представить как |
p |
|
i |
j |
, |
p* |
i |
j |
, i 1 3 |
в силу их комплексной |
||||||||||||
|
|
|
|
|
i |
|
|
|
i |
|
i |
i |
|
|
|
|
|
|
|
|
||
сопряжённости, где i и i |
- вещественная и мнимая (без учёта знака) часть комплексного |
|||||||||||||||||||||
полюса. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Полюса |
p являются попарно комплексно сопряжёнными - p |
|
и |
p |
p* , |
p и |
p p* , |
|||||||||||||||
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
2 |
1 |
3 |
4 |
3 |
p |
и p |
p* . Определим |
|
i |
и |
|
i |
- |
вещественную и мнимую (без учёта знака) |
часть |
||||||||||||
5 |
6 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
комплексного полюса: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
для |
p и |
p* вещественная часть |
1 |
0.31235 , мнимая часть |
1.1657 ; |
|
|
|||||||||||||||
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
6

для
p3
и
p |
* |
|
|
3 |
|
вещественная часть
|
2 |
|
0.85335
, мнимая часть
|
2 |
|
0.85335
;
для
p5
и p5*
вещественная часть
|
3 |
|
1.1657
, мнимая часть
|
3 |
|
0.31235
.
Подставим рассчитанные значения i и i в (1.6) и получим
e p1T e 1 j 1 T
e 1T cos 1T je 1T sin 1T 0.5502
j0.5856 ,
1
0.5502
,
1
0.5856
;
e |
p T |
e |
|
|
j |
T |
3 |
|
2 |
2 |
|
||
|
|
|
|
T |
T |
sin T 0.4547 |
||
e |
2 |
cos T je |
2 |
|
|
|
|
||
|
|
2 |
|
2 |
j0.3096
,
|
2 |
|
0.4547
,
|
2 |
|
0.3096
;
e p5T e 3 j 3 T
e 3T cos 3T je 3T sin 3T 0.4314
j0.0959 ,
|
3 |
|
0.4314
,
|
3 |
|
0.0959
;
Объедения попарно комплексно сопряжённые слагаемые в выражении (1.5) передаточной функции цифрового ФНЧ в виде суммы биквадратных звеньев
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N /2 |
|
|
b |
|
b |
|
z 1 |
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
H z |
|
|
0i |
|
|
|
|
1i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 a |
z |
1 |
a |
|
|
z |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1i |
|
|
|
|
|
|
|
2i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
где b |
2c , b |
2 c d |
, a |
2 , |
a |
|
|
2 |
|
2 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
0i |
|
i |
1i |
|
|
|
|
i |
i |
i |
i |
1i |
|
|
i |
|
2i |
|
|
i |
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для фильтра порядка N 6 |
имеем в три биквадратных звена вида |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
3 |
|
b |
|
b |
z 1 |
|
|
|
b |
b z 1 |
|
|
|
|
|
b |
|
|
b |
|
z 1 |
|
|
|
b |
b |
z 1 |
|
|
|||||||||||||
H z |
|
0i |
|
|
1i |
|
|
2 |
01 |
|
|
11 |
|
|
|
|
|
|
02 |
|
|
|
|
12 |
|
|
|
|
|
03 |
|
|
13 |
|
|
|
|
||||||
1 |
a |
|
z |
1 |
a |
z |
a |
z |
1 |
a |
z |
2 |
|
|
|
|
|
z |
1 |
a |
|
z |
2 |
a |
z |
1 |
a |
|
z |
2 |
|||||||||||||
|
i 0 |
|
|
|
1 |
|
|
|
1 a |
|
|
|
22 |
|
1 |
|
23 |
|
|||||||||||||||||||||||||
|
|
1i |
|
|
|
2i |
|
|
|
11 |
|
|
21 |
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
13 |
|
|
|
|
|
|
||||||
Коэффициенты фильтра равны:
придём к
(1.7)
. (1.8)
b01 2c1 0.4990 ,
b02
2c2
3.7244
, b03
2c3
3.2255
, b11 2 c1 1 d1 1 0.7806 ,
b12 |
2 c2 2 |
d2 2 1.6934 |
, |
|
b13 2 c3 3 d3 3 |
0.8557 , |
, |
||||||||
a |
2 |
|
0.9094 , a |
2 |
|
0.8629 , |
a |
|
2 |
|
2 |
0.6456 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
12 |
|
2 |
|
13 |
|
|
3 |
|
21 |
1 |
1 |
|
|
||
a23 |
2 |
|
2 |
0.1953 . |
|
|
|
|
|
|
|
|
|
|
|
3 3 |
|
|
|
|
|
|
|
|
|
|
|
||||
a11 2 1 |
1.1004 |
, |
||
2 |
|
2 |
0.3026 |
, |
a22 2 |
2 |
|||
Подставив рассчитанные коэффициенты в выражение (1.8) получим окончательное выражение передаточной характеристики синтезируемого фильтра
H z 3.0893 |
|
0.4990 0.7806z 1 |
|
|
3.7244 1.6934z 1 |
|
|
3.2255 0.8557z 1 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
1 1.1004z |
1 |
0.6456z |
2 |
1 0.9094z |
1 |
0.3026z |
2 |
1 0.8629z |
1 |
0.1953z |
2 |
|||||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
(1.9) |
|
|
|
|
|
|
|
|
|
ВАЖНО! Из общей формулы (1.7) и полученного выражения для передаточной характеристики цифрового БИХ фильтра (1.9) видно, что метод инвариантности ИХ приводит к параллельному соединению биквадратных звеньев, тогда как метод билинейного преобразования (см. лабораторную работу «Синтез цифровых БИХфильтров методом билинейного z - преобразования») приводит к каскадному
соединению звеньев.
Расчёт ЦФ по методу инвариантности ИХ закончен.
7
1.3Процедура проведения домашнего задания и рекомендации по численным
расчётам
В итоге, для расчёта передаточной функции цифрового ФНЧ по методу инвариантности ИХ студенту требуется выполнить следующие действия:
1.Выписать граничные частоты фильтра, частоту дискретизации, передаточную функцию АФП ФНЧ и соответствующие ей полюса из лабораторной работы «Синтез
2.
3.
цифровых БИХ-фильтров методом билинейного |
z - преобразования»; |
|
Рассчитать нормированный период дискретизации; |
|
|
Рассчитать по формуле (1.4) коэффициенты Ai , |
i 1 6 |
; |
4. Выделить вещественную и мнимую часть коэффициентов
Ai
-
c |
i |
|
и
d |
i |
|
, выделить
вещественную и мнимую части экспоненты e |
p T |
- |
i и i |
соответственно; |
|
i |
|||||
|
|
|
|
||
5. Рассчитать коэффициенты биквадратного звена b0i |
, b1i , a1i |
, a2i ; |
|||
6.Подставить рассчитанные коэффициенты биквадратного звена b0i , b1i , a1i , выражение для передаточной функции (1.8).
Домашний расчёт окончен.
a2i
в
2 Лабораторное задание
1.Собрать синтезированный в домашнем задании фильтр в среде имитационного моделирования РТС «Спектр-2» в виде параллельно соединённых биквадратных звеньев (каждое звено представляет собой прямую форму первого типа).
2.Снять основные характеристики собранного фильтра (амплитудно-частотную характеристику (АЧХ) в логарифмическом и линейном масштабе и ИХ).
3.По получившемуся графику АЧХ определить граничные значения частоты полосы пропускания и полосы задержания фильтра. Сравнить их с рассчитанными в домашнем задании.
4.Проанализировать характер ИХ.
5.Провести сравнение основных характеристик фильтра, синтезированного по методу билинейного z -преобразования и метода инвариантности ИХ при одних и тех же требованиях.
2.1Рекомендации к выполнению лабораторной работы
Необходимо запустить программу «Spectr-2» двойным нажатием левой кнопки мыши по исполняемому файлу Spectr2.exe. В открывшемся окне следует выбрать пункт меню «Файл» - «Собрать систему». После выполнения данных действий появится окно «Параметры системы», в которое требуется ввести частоту дискретизации и размер рабочего поля, измеряемое в количестве ячеек.
Открывается редактор систем, имеющий вид, представленный на рисунке 1:
8

Рисунок 1. Рабочее поле Спектр-2 Слева в редакторе схем находится дерево устройств. Чтобы собрать схему исследуемого
фильтра нужно выбрать папку «Временной тракт», в которой содержатся необходимые элементы. Во внутренней папке «Устройства обработки» находится сумматор, сумматор (3 вх) и усилитель. Из папки «Линии задержки» берётся линия задержки (ЛЗ). Требуемое количество элементов для рассчитанного в домашнем задании фильтра переносится на рабочее поле. ло
Также на рабочее поле ставится генератор тактовых импульсов, который берётся в папке «Вход» - «Генераторы» - ГТИ. ГТИ нужен для подачи на вход фильтра цифрового единичного импульса. Внутренние настройки ГТИ: период - размер пачки системы (см. свойства системы, по умолчанию 4096); ширина импульса - 1. После того, как все необходимые элементы введены на поле и расставлены, в верхнем левом углу необходимо нажать кнопку «Соединение устройств» и соединить между собой все элементы фильтра. То есть соединить все элементы биквадратного звена и сами биквадратные звенья между собой. Количество биквадратных звеньев определяется порядком фильтра n . В случае чётного порядка количество биквадратных звеньев n / 2 . Для анализа основных характеристик БИХ-фильтра необходимо ввести в схему спектроанализатор и осциллограф. Для этого нужно щёлкнуть по свободной клетке рабочего поля правой кнопкой мыши, выбрать «осциллограмма» («спектр»), в появившемся окне нажать «ОК». Спектроанализатор и осциллограф требуется поставить на выходе фильтра. Также, по желанию, можно поставить их на выходе ГТИ.
Когда схема фильтра собрана, в усилители записываются значения коэффициентов См. пример расчёта домашнего задания 1.2.
a
и b .
ВАЖНО!! Коэффициенты |
a |
(кроме |
a0 |
, который по умолчанию всегда равен 1) |
вносятся в усилитель со знаком противоположным рассчитанному.
Например, у первого биквадратного звена ФНЧ Баттерворта, рассчитанного выше, коэффициенты b равны b0 0.4990 , b1 0.7806 , а коэффициенты a равны a0 1
9

a1
1.1004
, a2
0.6456
. Тогда коэффициенты для первого звена необходимо ввести как
показано на рисунке 2. Для остальных биквадратных звеньев коэффициенты вводятся аналогично.
Рисунок 2. Первое биквадратное звено ФНЧ Чебышева
ВАЖНО! Метод инвариантности ИХ приводит к параллельному соединению биквадратных звеньев, а не каскадному как при синтезе БИХ фильтров методом билинейного z - преобразования.
Схема для ФНЧ Баттерворта представлена на рисунке 3, на котором отмечены:
1 - одно биквадратное звено;
1.1 - усилитель; 1.2-сумматор с тремя входами;
1.3– сумматор с двумя входами;
1.4- элемент линии задержки;
2 - генератор цифровых единичных импульсов;
3 - спектроанализатор и осциллограф.
10
