
LR_TsOS_5_KIKh_KAJZER
.pdf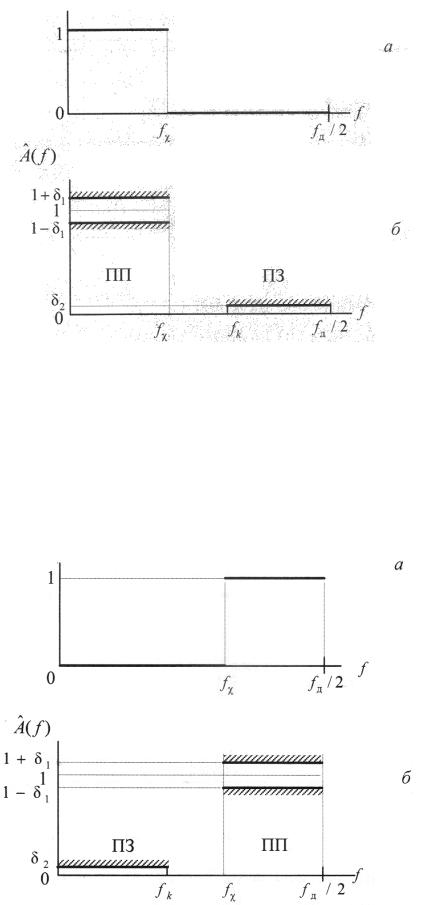
Рисунок 12. Идеальная АЧХ ФНЧ (а), требования к АЧХ ФНЧ (б) Требования могут задаваться к АЧХ в децибелах – к характеристике
ослабления:
ˆ |
|
|
ˆ |
A f |
|
20 lg A f |
|
|
дБ |
|
|
или к характеристике затухания: |
|
|
|
ˆ |
|
|
ˆ |
A f |
|
20 lg A f . |
|
дБ |
|
|
|
(25)
(26)
Рисунок 13. Идеальная АЧХ ФВЧ (а), требования к АЧХ ФВЧ (б)
21
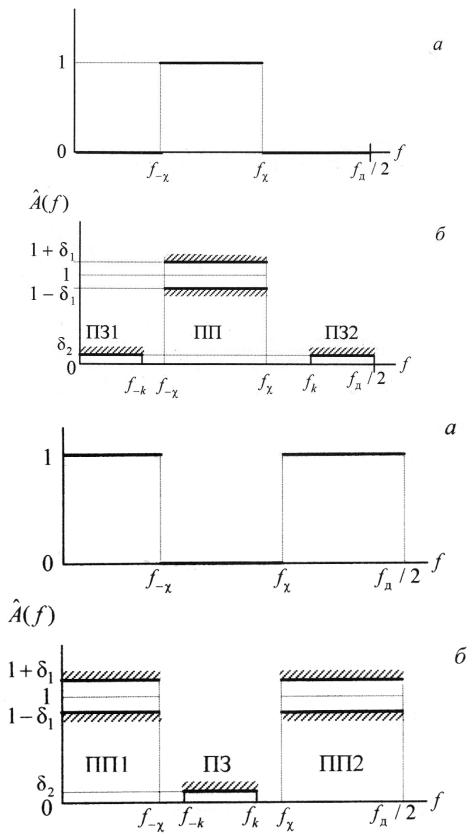
Рисунок 14. Идеальная АЧХ ПФ (а), требования к АЧХ ПФ (б)
Рисунок 15. Идеальная АЧХ РФ (а), требования к АЧХ (б) РФ (б)
22
В требованиях к характеристике максимально допустимых отклонений 1 ,
затухания
2 , 11 , 12 ,
(26)
21 ,
вместо значений 22 задаются:
|
a |
|
max дБ |
– максимально допустимое затухание в ПП (для ФНЧ, ФВЧ и ПФ);
|
a |
|
min дБ |
– минимально допустимое затухание в ПЗ (для ФНЧ, ФВЧ и РФ);
a1max дБ – максимально допустимое затухание в ПП1 (для РФ);
a2 max дБ – максимально допустимое затухание в ПП2 (для РФ);
|
a |
|
1min дБ |
– минимально допустимое затухание в П31 (для ПФ);
|
a |
|
2 min дБ |
– минимально допустимое затухание в П32 (для ПФ).
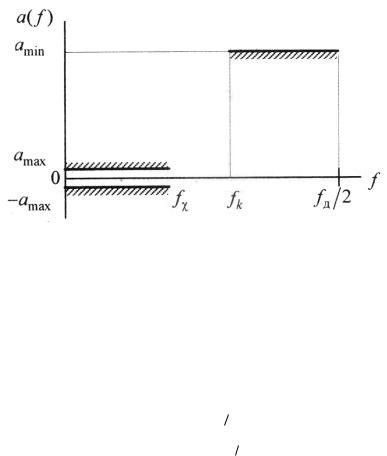
На рисунке 16 приведен пример требований к характеристике затухания ФНЧ.
Рисунок 16. Требования к характеристике затухания ФНЧ Взаимосвязь между значениями максимально допустимых отклонений
и их соответствующими значениями в децибелах, например, между 1 |
, и 2 и |
||||||
amax и amin |
устанавливается формулами: |
|
|
||||
|
amax 20 lg 1 1 дБ |
; |
(27) |
||||
|
am шт 20 |
lg 2 дБ , |
|
(28) |
|||
и наоборот: |
|
|
|
|
|
|
|
|
|
1 |
1 |
10 amax 20 ; |
|
(29) |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
1 |
10 amin 20 . |
|
(30) |
|
|
|
|
|
|
|
|
5.4 Синтез КИХ-фильтров методом окон
Среди достаточного разнообразия методов синтеза КИХ-фильтров наибольшее применение в различных приложениях получили два «классических»: метод окон и метод оптимального (по Чебышеву) синтеза.
23
5.4.1 Общая характеристика задачи синтеза КИХ-фильтров методом окон
Зададимся целью рассчитать коэффициенты (импульсную характеристику) одного из частотно-избирательных фильтров, представленных на рисунках 12 – 15, например ФНЧ.
Рассматриваемый фильтр имеет идеальную АЧХ, поэтому его частотная характеристика может быть представлена только бесконечным рядом Фурье:
|
и |
|
|
|
|
|
и |
|
|
|
j T |
|
|
j nT |
|||
H |
|
e |
|
|
|
|
h (n)e |
|
|
|
|
|
|
|
n |
|
|
,
(31)
где T |
– интервал дискретизации. |
|
|
|
|
|
||
|
Импульсная характеристика такого |
|||||||
формуле: |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
/2 |
|
|
|
|
|
|
д |
|
|
и |
|
|
|
и |
|
|
|
|
|
||
|
|
|
|
|
|
|||
|
h |
(n) |
|
|
|
H |
|
e |
|
|
|
|
|
/2 |
|
|
|
|
|
|
д |
|
|
|
||
|
|
|
|
д |
|
|
|
|
фильтра может быть найдена по
j T |
e |
j nT |
d , |
(32) |
|
|
где д – угловая частота ФНЧ с частотой среза с
дискретизации д |
2 T |
1 |
|
|
|||
2 fc |
АЧХ имеет вид: |
|
|
рад/с. Для идеального
|
|
|
|
|
|
|
|
|
j T |
|
|
1, |
|
, |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
Hи e |
|
|
|
|
|
|
с |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
с . |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
0, |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тогда ИХ найдется в форме: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin |
nT |
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
1 |
c |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
h |
(n) |
|
e |
j nT |
d |
|
|
e |
j nT |
e |
j nT |
|
|
c |
||||||||||
|
|
|
|
|
|
|
c |
|
|
c |
|
c |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
j nT |
|
|
|
|
|
|
|
|
|
|
|
nT |
|
|||
|
|
|
|
д |
c |
|
|
д |
|
|
|
|
|
|
|
|
|
|
|
д |
|
c |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
sinc nT |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
2 |
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
д |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где sinc x sin x / x . Выражение (34) можно переписать в форме:
|
|
|
ˆ |
, |
|
|
|
|
|
2 f |
|
|
|
||
|
|
|
c |
|
|
|
|
h |
(n) |
|
|
|
ˆ |
|
|
sin |
|
|
|
||||
и |
|
2 fcn |
|||||
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
||
где |
|
|
|
|
|
|
|
|
|
|
ˆ |
|
|
c |
|
|
|
|
fc |
|
|||
|
|
|
|
|
|
д |
|
– нормированная частота среза.
n 0,
, n 0, n 0
fc , fд
(33)
(34)
(35)
Ясно, что это – физически нереализуемый БИХ-фильтр, поскольку импульсная характеристика бесконечна и начинается в минус бесконечности,
24
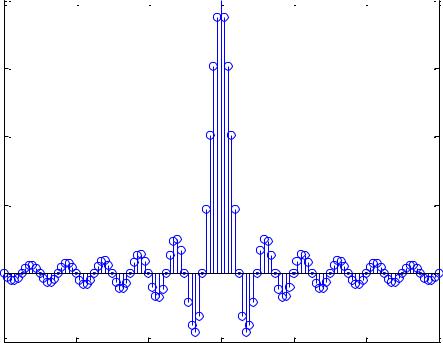
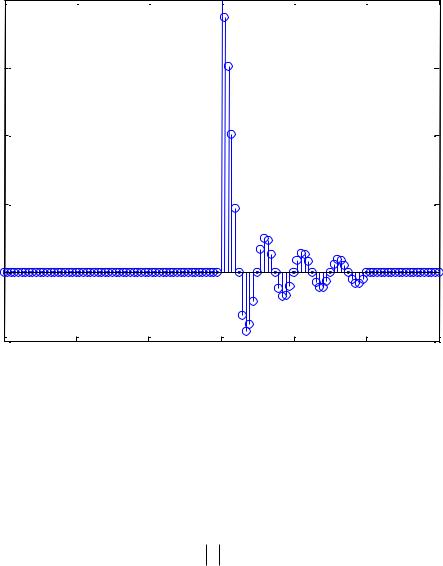
то есть реакция будет предшествовать воздействию (см. рисунок 17). Простейший путь конструирования физически реализуемой передаточной функции фильтра состоит в исключении всех членов ряда (31) (т.е. элементов последовательности (35)), имеющих отрицательный индекс. В результате получается импульсная характеристика, соответствующая БИХ-фильтру. Для получения импульсной характеристики КИХ-фильтра необходимо ограничить ряд (31) сверху до N+1 членов. Однако, при такой последовательности действий нарушается симметрия ИХ, а значит и линейность ФЧХ полученного фильтра (см. рисунок 18). Поэтому обычно поступают следующим образом: ограничивают ряд (31) (т.е.
последовательность (35)) |
в |
симметричных |
пределах относительно нуля |
(например, от N 1 / 2 |
до |
N 1 / 2 ), а |
затем полученную конечную |
последовательность сдвигают таким образом, чтобы первый отличный от нуля отсчеты имел индекс n = 0. Изложенное иллюстрируется рисунком 19.
ИХ идеального фильтра 0.2 






0.15
0.1
hi(n)
0.05 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
-0.05 |
|
|
|
|
|
|
-60 |
-40 |
-20 |
0 |
20 |
40 |
60 |
|
|
|
n |
|
|
|
Рисунок 17. Бесконечная импульсная характеристика идеального ФНЧ
25
ИХ идеального фильтра усеченная 0.2 





0.15
0.1
hy(n)
0.05 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
-0.05 |
|
|
|
|
|
|
-60 |
-40 |
-20 |
0 |
20 |
40 |
60 |
|
|
|
n |
|
|
|
Рисунок 18. Усеченная ИХ физически реализуемого КИХ-фильтра
n
ИХ идеального
20, 19,..., 1,0,1,...,19,
фильтра
20 .
усекается до длины Усечение эквивалентно
N 41 |
, |
поотсченому
умножению ИХ идеального фильтра на конечную симметричную оконную последовательность (прямоугольное окно):
1, n 20, w(n)
. (36)
0,  n
n 20
20
Далее полученная таким образом усеченная ИХ сдвигается вправо в область положительных индексов таким образом, чтобы первый отличный от
нуля отсчет имел индекс |
n 0 |
. ИХ изображены для фильтра с |
нормированной частотой среза |
ˆ |
0.1 |
fc |
,частота дискретизации fд 48000Гц ) .
(реальная частота среза
f |
c |
4800 Гц |
|
|
Сдвиг последовательности вправо эквивалентен задержке на сдвигаемое количество отсчетов. Задержка во временной области приводит к появлению множителя с линейным фазовым сдвигом, что не нарушает линейности ФЧХ фильтра. Полученные после усечения и сдвига отсчеты h(n) используются в качестве коэффициентов КИХ-фильтра:
b(i) h(i), i 0,1,..., 41.
26
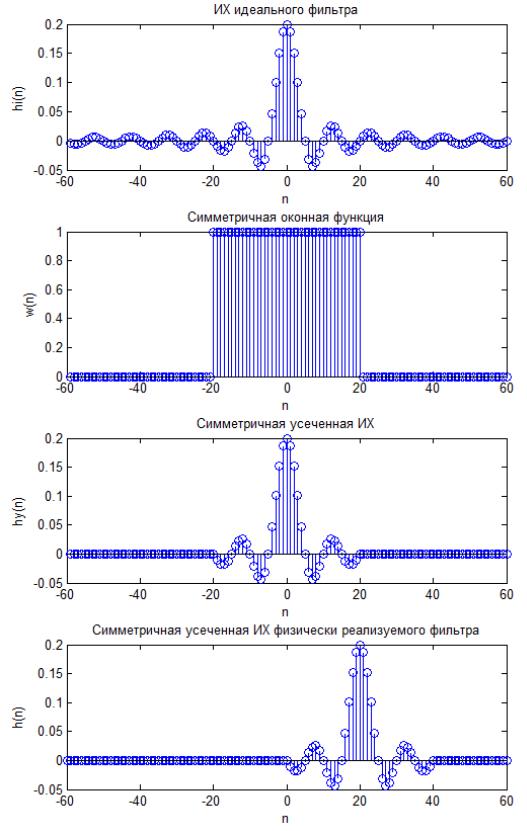
Рисунок 19. Сверху вниз: 1) ИХ идеального ФНЧ, 2) симметричная оконная последовательность (прямоугольное окно), 3) симметричная усеченная ИХ, 4) симметричная усеченная ИХ физически реализуемого фильтра
27
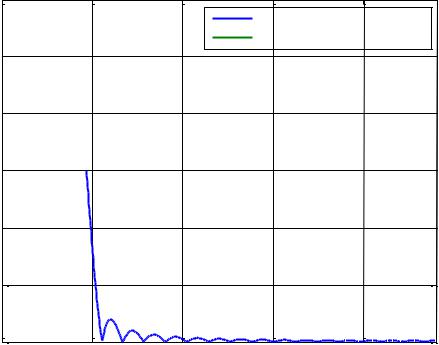
На рисунке 20 изображены АЧХ идеального и реального ФНЧ. Видно, что АЧХ реального фильтра аппроксимирует АЧХ идеального фильтра. Обе кривых пересекаются в точке, соответствующей частоте среза fc 4800 Гц (АЧХ на частоте среза равно 0.5). При этом у АЧХ реального фильтра наблюдаются отклонения колебательного характера от АЧХ идеального фильтра, как в полосе пропускания, так и в полосе задержания.
H(exp(jwT))
АЧХ КИХ R = 40-го порядка АЧХ идеального ФНЧ
1
0.8
0.6
0.4
0.2
00 |
0.5 |
1 |
1.5 |
2 |
|
|
|
f, Гц |
4 |
|
|
|
|
x 10 |
Рисунок 20. АЧХ идеального и реального ФНЧ |
|
|
Казалось бы, решение найдено. Действительно, подбирая значения |
N |
|
и контролируя поведение АЧХ, за несколько итераций можно найти такое |
N |
, |
при котором требования к заданному фильтру будут выполнены.
Однако усечение ряда Фурье вследствие разрывности АЧХ приводит к существенным ошибкам.
5.4.2Явление Гиббса
Появляющиеся ошибки связаны с характером сходимости ряда Фурье в
точке разрыва частоте среза f
c
первого рода, каковой и является точка, соответствующая (см. рисунок 20).
Во-первых, в точке разрыва
f |
c |
|
первого рода ряд Фурье сходится к
среднему предельных значений функции слева и справа. Предел слева
28
равняется 1 (АЧХ в полосе пропускания), задержания), тогда
H e |
j T |
0.5 . |
|
c |
|||
|
|
а справа 0 (АЧХ в полосе
(37)
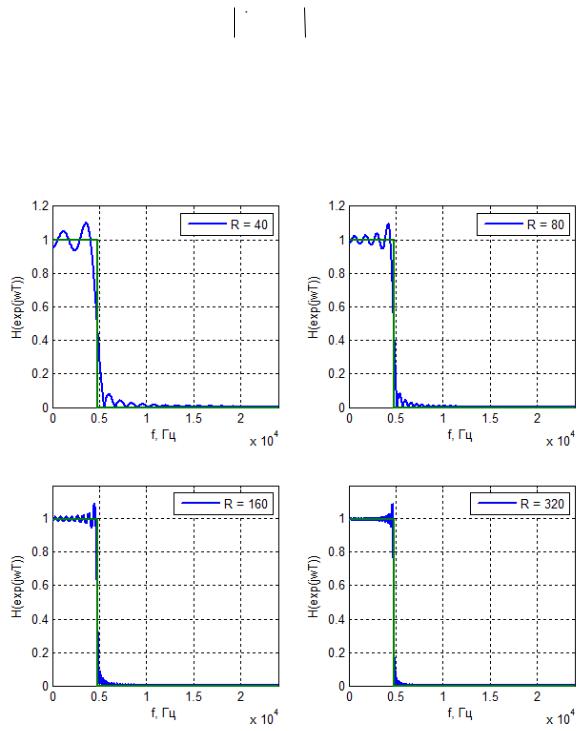
Во-вторых, в точке разрыва сходимость ряда Фурье не является равномерной и носит особый характер, который выражается в появлении пульсаций вблизи точки разрыва, максимум которых слева и справа составляет порядка 9% от АЧХ и остается таковым вне зависимости от порядка фильтра R (см. рисунок 21). Этот феномен получил название явления Гиббса.
Рисунок 21. АЧХ КИХ-фильтров различного порядка, иллюстрирующие явление Гиббса
В результате формируются пульсации как в полосе задержания, так и в полосе пропускания фильтра; кроме того образуется переходная полоса, ширина которой тем меньше, чем больше порядок фильтра R (см. рисунок
21).
29

Рассмотрим характеристика h(
n)
явление Гиббса более подробно. Импульсная проектируемого фильтра может быть записана в форме:
h(n) hи (n)w(n) , |
(38) |
где hи (n) – бесконечная ИХ идеального фильтра, w(n) |
– конечная оконная |
последовательность. Выражение (38) соответствует произведению двух последовательностей. Тогда, переходя в частотную область, получим:
|
|
|
|
|
|
/2 |
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
1 |
д |
|
|
|
|
e j u T |
|
|
|
H |
|
e j T |
|
|
|
H |
|
e juT W |
|
|
du |
|||
|
|
|
|
|
|
|
/2 |
|
|
|
|
|
|
|
|
|
|
|
|
д |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
д |
|
|
|
|
|
|
|
|
Выражение (39) (с |
|
учетом |
периодичности |
|
с |
периодом |
||||||||
д
(39)
частотных
характеристик дискретных систем и спектров дискретных сигналов)
описывает |
циклическую |
(круговую) |
|
|
свертку |
спектральной плотности |
|||||||||
оконной |
последовательности |
W e |
j T |
|
и |
частотной |
характеристики |
||||||||
|
|
||||||||||||||
идеального |
фильтра Hи e |
j T |
|
. Найдем |
|
|
|
спектральную плотность оконной |
|||||||
|
|
|
|
||||||||||||
последовательности длины |
N R 1 (полагая порядок фильтра R четным): |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
R 1 |
|
|
||
|
|
|
|
R/2 |
|
|
|
|
sin |
2 |
|
T |
|
||
|
W e j T |
e j nT |
|
|
|
|
|
|
|
(40) |
|||||
|
|
|
|
|
|
||||||||||
|
|
|
|
T |
|
||||||||||
|
|
|
n R/2 |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
sin |
2 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Выражение (40) известно как ядро Дирихле (см. рисунок 22). Это
колеблющаяся функция с максимальным значением |
N R 1 |
при |
0 . |
Область которой с максимальной амплитудой называется главным лепестком, а остальные области – боковыми лепестками. Очевидно, что функция W e j T принимает нулевые значения на частотах:
|
ˆ |
T k |
2 |
, |
(41) |
|
|
|
|||||
|
k |
k |
R 1 |
|
||
|
|
|
|
|||
а ширина всех лепестков, включая главный, одинакова и равна |
|
|||||
|
ˆ T |
2 |
. |
(42) |
||
|
|
|||||
|
|
|
R 1 |
|
||
Причем с увеличением R |
ширина главного лепестка уменьшается, а число |
|||||
боковых лепестков увеличивается. |
|
|
|
|
||
30
