2.16 Каноническая структура операционного автомата.

Операционный автомат (ОА) оценивается по следующим параметрам: производительность, быстродействие, сложность и однородность. Структура ОА зависит от класса задач, которые он решает.

Структура ОА определяется следующим образом:

1. Внутреннее состояние представлено набором регистров, соответствующих словам операционного автомата.

2. Входные слова связаны с входными полюсами.

3. Выходные слова соответствуют выходным полюсам.

4. Микрооперации и логические условия представлены комбинационными схемами.

Каноническая структура ОА достигается заменой каждого элемента функции соответствующими элементами структурного базиса, такими как регистры и комбинационные схемы.

Эта структура имеет следующий вид:

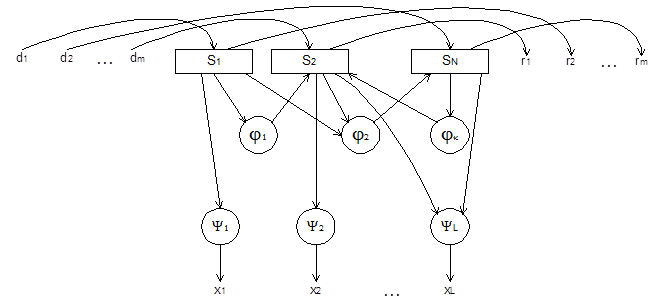
Пути оптимизации затрат оборудования включают:

1. Реализацию однотипных микроопераций на общих комбинационных схемах.

2. Объединение комбинационных схем для каждого элемента памяти.

Это позволяет повысить эффективность использования ресурсов и уменьшить сложность структуры ОА.

2.17 Гонки в автоматах и методы их устранения.

При функционировании автомата могут возникать состязания из-за различных времен срабатывания элементов памяти и задержек сигналов. Это может привести к нежелательным переходам и нарушению работы автомата. Гонки могут быть критическими и некритическими. Для ликвидации гонок используются аппаратурные методы, такие как двойная память и тактирование входных сигналов, а также методы кодирования, например, противогоночное кодирование и соседнее кодирование.

Таким образом, имеются 4 способа устранения гонок:

- двойная память;

-рациональный выбор длительности синхроимпульса;

- развязывание пар переходов;

- соседнее кодирование.

- укороти текст не теряя смысла

Один из способов ликвидации гонок состоит в тактировании входных сигналов автомата импульсами определенной длительности. Предполагается, что кроме входных полюсов x1,…, xl имеется еще один полюс р от генератора синхроимпульсов (ГСИ), по которому поступает сигнал р = 1 в момент прихода импульса и р = 0 при его отсутствии. В связи с этим на переходе (аm, аS) входным сигналом будет не z, а рz. Тогда, если длительность импульса меньше самого короткого пути прохождения тактированного сигнала обратной связи по комбинационной схеме, то к моменту перехода в промежуточное состояние аk сигнал р равен нулю и, следовательно, рz = 0, что и исключает гонки.

Другой способ ликвидации гонок заключается во введении двойной памяти. В этом случае каждый элемент памяти дублируется, причем перепись из нижнего элемента памяти в верхний происходит в момент отсутствия тактирующего импульса (р=0). Сигналы обратной связи для получения функций возбуждения и функций выходов автомата снимаются с верхнего ряда триггеров.

Таким образом, состязания могут возникнуть только между нижними триггерами, сигналы обратной связи не смогут измениться до тех пор, пока р не станет равным нулю. Но тогда входной сигнал рzf также равен нулю, а потому гонок быть не может.

Наряду с аппаратурными способами для устранения гонок могут использоваться специальные методы кодирования, которым посвящено большое число работ. Например, предлагается метод противогоночного кодирования, основная идея которого сводится к следующему: пусть (a,b) и (c,d) - две пары двоичных кодов длиной m. Пары (a,b) и (c,d) называются развязанными, если при некотором 1 ≤ r ≤mr -й разряд кода принимает одно значение на паре (a,b) и противоположное на паре (c,d). В противном случае пары двоичных кодов (a,b) и (c,d) называются связанными.