Как ставится и решается задача синтеза комбинационных схем.
Задача синтеза комбинационной схемы состоит в построении схемы для заданной булевой функции или системы булевых функций на основе определенной системы логических элементов. Как правило, исходное описание для синтеза схемы задается либо в виде таблицы истинности, либо в аналитической форме в виде системы.
На основе физического описания схемы строится таблица истинности, в которой каждому набору сигналов на входах схемы ставится в соответствие выходной сигнал. По этой таблице составляется система логических функций (ЛФ):
Система ЛФ, минимизируется любым классическим методом в заданном базисе.
П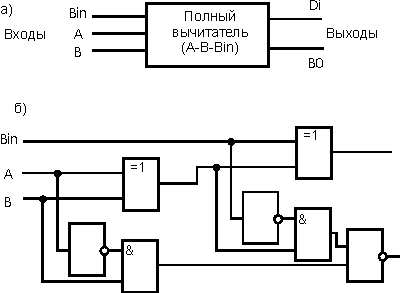
о
МДНФ или скобочной форме строится
логическая схема уст-ройства.
Канонический синтез одноразрядного полного двоичного сумматора.
Для создания одноразрядного полного двоичного сумматора можно использовать следующую схему:
Используйте два полу-сумматора для суммирования двух битов (A и B).
Результат суммирования этих двух битов будет представлен двумя битами: младший бит суммы (S) и перенос (C).
Для вычисления младшего бита суммы (S) используйте операцию исключающего ИЛИ между входными битами A и B.
Для вычисления переноса (C) используйте операцию И между входными битами A и B.
Таким образом, выходы S и C будут представлять собой результат Вот алгоритм для построения одноразрядного полного двоичного сумматора:
Примите два входных бита A и B.
Используйте операцию исключающего ИЛИ (XOR) для вычисления младшего бита суммы (S): S = A XOR B.
Используйте операцию И (AND) для вычисления переноса (C): C = A AND B.
Верните пару значений (S, C), где S - младший бит суммы, а C - перенос. Этот алгоритм создает полный двоичный сумматор, который может сложить два одноразрядных числа и выдать результат в виде младшего бита суммы (S) и переноса (C), который используется для сложения более старших разрядов в многоразрядном сумматоре. суммы и перенос соответственно.
П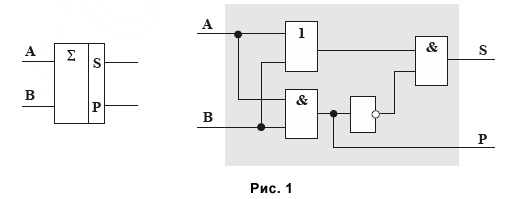
остроим
таблицу истинности для устройства
реализующего арифметическую операцию
сложения. Операция «+» бинарная, поэтому полусумматор должен иметь два входа (A и B). В результате сложения двух одноразрядных двоичных чисел может получиться двухразрядное число (с переносом в следующий разряд). Значит, устройство должно иметь два выхода (P - перенос в следующий разряд, S - результат, остающийся в текущем разряде).
A B P S
0 0 0 0
0 1 0 1
1 0 0 1
1 1 1 0
По данной таблице истинности построим СДНФ
Для переноса в старший разряд: P = A ∧ B
Для текущего разряда: S = ¬ A ∧ B ∨ A ∧ ¬ B
Преобразуем логическую формулу для S: (¬ A • B) + (A • ¬ B) = (¬ A • A) + ( ¬ A • B) + (A • ¬ B) + (¬ B • B) = = ¬ A • (A + B) + ¬ B • (A + B) = (A + B) • ¬ (A • B)
С учетом формулы для переноса имеем: S = (A + B) • ¬ (A • B) = (A + B) • ¬ P
1.3.Канонический синтез одноразрядного полного двоичного вычитателя.
Для создания одноразрядного полного двоичного вычитателя можно использовать следующую схему: Используйте два полу-вычитателя для вычитания второго бита из первого (A и B). Результат вычитания этих двух битов будет представлен двумя битами: младший бит разности (D) и заем (Borrow). Для вычисления младшего бита разности (D) используйте операцию исключающего ИЛИ между входными битами A и B. Для вычисления заема (Borrow) используйте операцию НЕ для инвертирования второго входного бита B, а затем примените операцию И между инвертированным значением B и первым входным битом A. Таким образом, выходы D и Borrow будут представлять собой результат вычитания и заем соответственно.