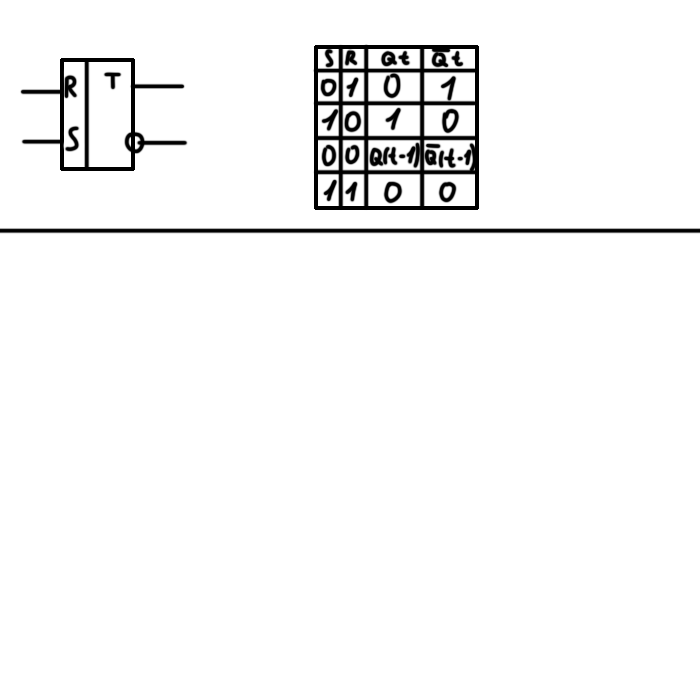
2.13 Разновидности элементарных цифровых автоматов (триггеров). Привести примеры.

Элементарные цифровые автоматы, или триггеры, представляют собой основные строительные блоки в цифровой логике и используются для хранения одного бита информации.

Асинхронный триггер изменяет своё состояние непосредственно в момент появления соответствующего информационного сигнала

Синхронные триггеры с динамическим тактированием изменяют своё состояние только в момент определённого перехода тактового сигнала Типы:

RS-триггер - асинхронный триггер, который сохраняет своё предыдущее состояние при неактивном состоянии обоих входов и изменяет своё состояние при подаче на один из его входов активного уровня.

______

S --| |--- Q

| RS |

R --|_____|--- /Q

D-триггер - запоминает состояние входа и выдаёт его на выход.

D Q(t) Q(t+1)

0 0 0

0 1 0

1 0 1

1 1 1

Т-триггер он является простейшим счётчиком по модулю 2. После поступления на вход "T" импульса, состояние триггера меняется на прямо противоположное.

____

T -- -| |--- Q

| T |

CLK -|____|--- /Q

JK триггер - работает так же как RS-триггер, но при подаче логической единицы на оба входа J и K состояние выхода триггера изменяется на противоположное, то есть выполняется операция инверсии

J K Q(t) Q(t+1)

0 0 0 0

0 0 1 1

0 1 0 0

0 1 1 0

1 0 0 1

1 0 1 1

1 1 0 1

1 1 1 0

2.14 Канонический синтез микропрограммного управляющего автомата по модели Мили.

Для построения канонического синтеза УА по Мили, нужно для начала сделать разметку графической схемы автомата по состояниям.

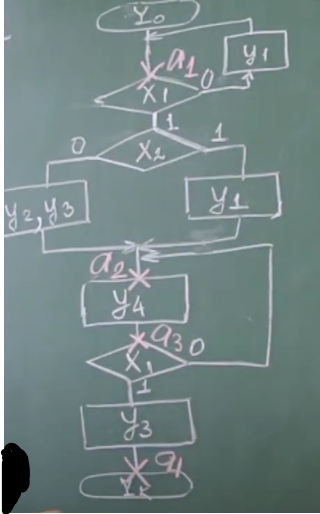
Затем по выделенным состоянием начинаем заплнять таблицу переходов, учитывая состояния и микрооперации между ними

2.15 Канонический синтез микропрограммного управляющего автомата по модели Мура.

Канонический синтез микропрограммного управляющего автомата по модели Мура включает в себя несколько этапов:

1. Определение состояний автомата: Начинается с определения всех возможных состояний автомата на основе его спецификаций и требований к функционированию.

2. Разметка состояний: Каждому состоянию присваивается уникальная метка, которая будет использоваться для дальнейшей работы.

3. Анализ переходов: Изучаются возможные переходы между состояниями автомата на основе его структуры и задач, которые он должен выполнять.

4. Формирование обратной структуры и таблицы переходов: Строится таблица, которая описывает переходы между состояниями автомата и условия, при которых эти переходы происходят. Эта таблица может быть упорядочена по состояниям или по условиям, в зависимости от удобства анализа.

5. Кодирование состояний: Каждому состоянию присваивается уникальный код, который будет использоваться для управления автоматом.

6. Формирование уравнений для функции переходов: На основе таблицы переходов формулируются уравнения, которые определяют условия перехода между состояниями автомата.

7. Реализация и тестирование: Полученные уравнения используются для разработки программы управления автоматом, которая затем тестируется на соответствие требованиям и корректность работы.

Таким образом, канонический синтез микропрограммного управляющего автомата по модели Мура включает в себя анализ, проектирование и реализацию управляющей программы, основанной на заданных условиях и требованиях к автомату.