



Рис. 9.11. Эквивалентные схемы полупроводникового диода в двух состояниях: а – управляющий ток подан; б - управляющий ток отсутствует
На рис. 9.12, 9.13 приведены некоторые результаты моделирования на ЭВМ одноступенчатого отражательного фазовращателя [(9.17)-(9.21)] при следующих исходных данных:  =1 Ом,
=1 Ом,  = 0,2 пФ,
= 0,2 пФ,  =2 Ом и
=2 Ом и  =50 Ом. На рис. 9.12 можно определить значения характеристического сопротивления
=50 Ом. На рис. 9.12 можно определить значения характеристического сопротивления  и электрической длины
и электрической длины  трансформирующего отрезка длинной линии, обеспечивающей требуемый дискрет фазы
трансформирующего отрезка длинной линии, обеспечивающей требуемый дискрет фазы  . Экстремальные точки кривых на этом рисунке определяют оптимальные значения параметров
. Экстремальные точки кривых на этом рисунке определяют оптимальные значения параметров  и
и  , обеспечивающие минимальное изменение
, обеспечивающие минимальное изменение  в диапазоне частот. Например, для
в диапазоне частот. Например, для
 =180°
=180°  =33 Ом,
=33 Ом,  =122°, для
=122°, для  =90°
=90° 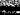 =29 Ом,
=29 Ом,  =33° и
=33° и  =60 0м,
=60 0м,  =120°, для
=120°, для  =45° имеем
=45° имеем  =92 Ом,
=92 Ом,  =110°. Как видно из рис. 9.12, для неко-
=110°. Как видно из рис. 9.12, для неко-
торых фазовых сдвигов  может быть получено до четырех решений, определяющих топологию схемы фазовращателя.
может быть получено до четырех решений, определяющих топологию схемы фазовращателя.
 Рис. 9.12. Зависимость фазы фазовращателя от 1
Рис. 9.12. Зависимость фазы фазовращателя от 1
Графики на рис. 9.13 позволяют определить для всех конструкций фазовращателя, в том числе и оптимальных, модули коэффициентов отражения для открытого  и закрытого
и закрытого  состояний диода, а, следовательно, и потери.
состояний диода, а, следовательно, и потери.
8
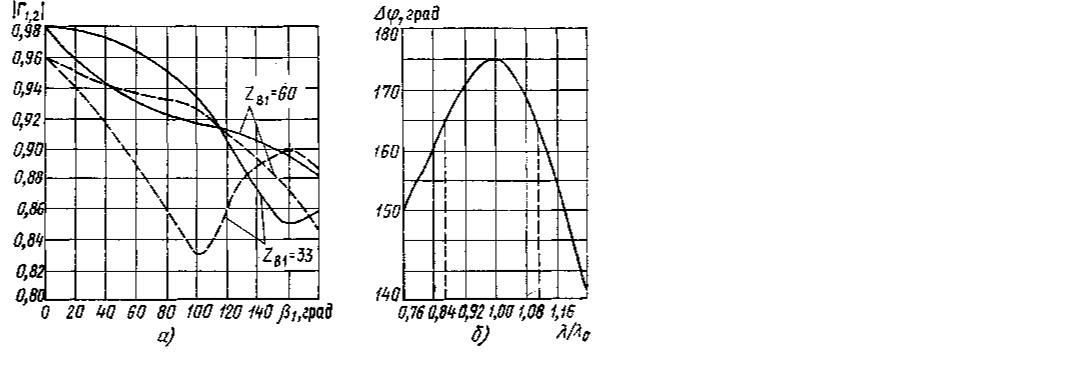
Рис. 9.13. Параметры фазовращателя: а – коэффициент отражения; б – фазовый сдвиг
Так, для  =180°
=180°  =0,86 и
=0,86 и  =0,9, а для
=0,9, а для  =90°
=90°  =0,94 и
=0,94 и  =0,97. Потери в этом случае соответственно равны 1,3 и 0,64 дБ. Наконец, на рис. 9.13,б представлена зависимость изменения оптимального фазового дискрета
=0,97. Потери в этом случае соответственно равны 1,3 и 0,64 дБ. Наконец, на рис. 9.13,б представлена зависимость изменения оптимального фазового дискрета  =180° от частоты, из которой видно, что при ±10%-ных расстройках фаза изменяется лишь на 10°.
=180° от частоты, из которой видно, что при ±10%-ных расстройках фаза изменяется лишь на 10°.
Многоступенчатые отражательные фазовращатели строятся по принципу последовательного соединения нескольких одноступенчатых ОФ. Поэтому их моделирование практически ничем не отличается от моделирования одноступенчатого ОФ. Проектирование реальных PC ФАР, состоящих из сотен и тысяч излучателей, осуществляется на ЭВМ на основании разработанной математической модели. При этом с учетом выбранных базовых элементов определяется
ожидаемый закон АФР возбуждения  , его отличие от требуемого. Если необходимо, следует изменить характеристики тех или иных устройств СВЧ. Отметим следующие важные для практики особенности разработанной модели PC:
, его отличие от требуемого. Если необходимо, следует изменить характеристики тех или иных устройств СВЧ. Отметим следующие важные для практики особенности разработанной модели PC:
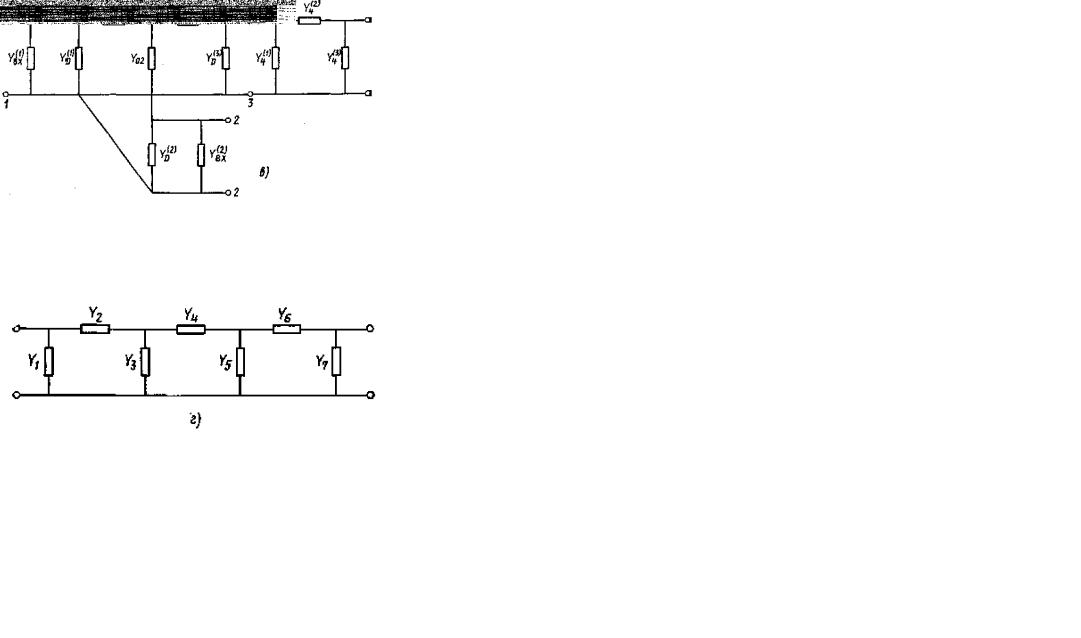
1)автоматически учитывается взаимовлияние всех каналов PC, так как электродинамическая информация о них передается через входные проводимости, подключаемые к анализируемому каналу через MD на различных этажах (это легко проследить с помощью рис. 9.5);
2)зная функции изменения проводимостей и ДН излучателей при сканировании ФАР, можно рассчитать ожидаемые АФР  и соответствующие им ДН решетки в рабочем секторе углов;
и соответствующие им ДН решетки в рабочем секторе углов;
3)открывается возможность для решения актуальной задачи автоматизированного проектирования по требуемому АФР возбуждения  в раскрыве антенны и выбранной схеме PC оптимальных проводимостей базовых элементов;
в раскрыве антенны и выбранной схеме PC оптимальных проводимостей базовых элементов;
4)эта модель полностью применима и для анализа ФАР, в каждом модуле которой имеется свой генератор; в этом случае, как видно из структурной схемы рис. 9.6, весь расчет сводится, по существу, к уже известной задаче моделирования нулевого этажа с использованием затем формул (9.9)-(9.13).
9




 (9.13)
(9.13) рассчитанной по формуле типа (9.13) с использованием соотношений (9.11), (9.12).
рассчитанной по формуле типа (9.13) с использованием соотношений (9.11), (9.12). .
. и
и  первого и второго каналов нулевого этажа и линии
первого и второго каналов нулевого этажа и линии  подключены соответственно к полюсам 1-1,
подключены соответственно к полюсам 1-1,  -параметров:
-параметров: 

 соответствующими схемами замещения, получаем схему рис. 9.9,б, описывающую первый этаж и его связь с нулевым и вторым этажами. Преобразуем треугольник, образованный проводимостями
соответствующими схемами замещения, получаем схему рис. 9.9,б, описывающую первый этаж и его связь с нулевым и вторым этажами. Преобразуем треугольник, образованный проводимостями  в звезду. Проводимости
в звезду. Проводимости  последней определяются:
последней определяются:

 (9.15)
(9.15)
 (9.16)
(9.16) и
и  представляют входные проводимости каналов предыдущего этажа, подключенных к
представляют входные проводимости каналов предыдущего этажа, подключенных к  последнего этажа для каждого
последнего этажа для каждого  , реализуемый PC в раскрыве антенны. Для этого представим генератор в виде четырехполюсника с известной матрицей
, реализуемый PC в раскрыве антенны. Для этого представим генератор в виде четырехполюсника с известной матрицей  -параметров и подставим в (9.4)
-параметров и подставим в (9.4)  вместо
вместо Тогда получим
Тогда получим – напряжение генератора;
– напряжение генератора;  и
и  – параметры его матрицы.
– параметры его матрицы.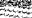 , естественно, в общем случае будет отличаться, от требуемого закона возбуждения
, естественно, в общем случае будет отличаться, от требуемого закона возбуждения  . Чтобы реализовать АФР
. Чтобы реализовать АФР  , необходимо, как видно из приведенной выше формулы, подобрать БЭ PC с вполне определенными значениями
, необходимо, как видно из приведенной выше формулы, подобрать БЭ PC с вполне определенными значениями  -параметров. Эту задачу моделирования можно решать в интерактивном, режиме с помощью разработанной выше модели PC, целенаправленно изменяя
-параметров. Эту задачу моделирования можно решать в интерактивном, режиме с помощью разработанной выше модели PC, целенаправленно изменяя  -параметры БЭ, например, нулевого этажа (соединительных линий, Ф и т. п.).
-параметры БЭ, например, нулевого этажа (соединительных линий, Ф и т. п.). =5...200 кВт,
=5...200 кВт,  =5...50 Вт), малое время переключения (0,1...100 мкс), минимальные потери (0,1...1 дБ), хорошее согласование (КСВ<=1,5).
=5...50 Вт), малое время переключения (0,1...100 мкс), минимальные потери (0,1...1 дБ), хорошее согласование (КСВ<=1,5). коэффициента отражения ОФ при двух состояниях полупроводникового диода. Известно, что эти два состояния характери-
коэффициента отражения ОФ при двух состояниях полупроводникового диода. Известно, что эти два состояния характери- и
и  составляют соответственно единицы, единицы - десятки Ом и единицы пикофарад. Таким образом, фазовый дискрет Δφ является функцией от
составляют соответственно единицы, единицы - десятки Ом и единицы пикофарад. Таким образом, фазовый дискрет Δφ является функцией от  и параметров
и параметров  и
и  :
: 

 и
и  – соответственно волновое сопротивление и длина соединительной линии
– соответственно волновое сопротивление и длина соединительной линии  (9.17)
(9.17) (9.18)
(9.18) (9.19)
(9.19) проводимость этой цепочки определяется формулой типа (9.13), а коэффициент отражения
проводимость этой цепочки определяется формулой типа (9.13), а коэффициент отражения (9.20) поэтому
(9.20) поэтому  (9.21)
(9.21) и
и  - значения коэффициента отражения, соответствующие двум состояниям диода.
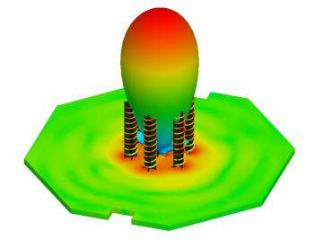
- значения коэффициента отражения, соответствующие двум состояниям диода. Модель антенны, установленной на истребитель-бомбардировщик F-35. ДН излучения
Модель антенны, установленной на истребитель-бомбардировщик F-35. ДН излучения