862

Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Пермский Государственный аграрно-технологический университет им. Д.Н. Прянишникова

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

D t 2 f (t)dt M 2 t 2е t

.pdf

Скачиваний:

Добавлен:

09.01.2024

Размер:

6.93 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 1213 / 2213 14 15 16 17 18 19 20 21 22 > Следующая >>>

121

Рис. 5.8. Схема к выводу уравнения распределения семян в рядке в случае нецелого числа суммируемых отрезков t

Для определения закона распределения расстояний Т в этом случае нужно дополнительно определить распределение отрезков AB и BC.

Пусть, например, промежуток ti, с функцией распределения

F(t) 1 е t

продолжался некоторое время η (рис.5.9) т.е. произошло событие ti > η.

Рис.5.9. Схема к определению распределения участков η и Т1

Условный закон распределения оставшейся части промежутка Т1=ti- η обозначен как F(η)(t)

	( )		t t
F		(t) P (ti )	t t	i	.
				i

Для вычисления F(η)(t) необходимо найти вероятность одновременного наступления событий

		ti и					(ti ) t .
По теореме умножения вероятностей
P (t ) (t t) P(t ) P(t t								) P(t ) F ( ) (t) ,
i	i		i			i		ti	i
i	i		i			i			i
откуда					P (ti	)(ti t) .
		F ( ) (t)			P (ti
		F ( ) (t)
						P(ti )
Но событие ( ti ) ( ti				t ) равносильно
				ti		t ,

вероятность которого равна

P( ti ) F(t ) F( ) .

С другой стороны,

P(ti ) 1 F( )

следовательно,
F ( ) (t)	F (t ) F ( )	.

	1 F ( )

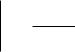
122

Откуда, согласно (5.4) можно получить

F ( ) (t)	е	е (t )	1 е t F(t) .
		е t

Таким образом, условный закон распределения вероятностей F ( ) (t)

не зависит от η и равен F(t), иначе говоря, любая точка внутри промежутка ti, распределенного по показательному закону, делит этот промежуток на две части, каждая из которых является отрезком, распределенным по тому же закону, т.е. с любой частью отрезка ti можно оперировать как с целым.

Плотность распределения промежутков Т можно найти как композицию k + 1 отрезка с распределением (5.5).

Для определения такой композиции удобно воспользоваться свойствами характеристических функций θ(х). Характеристической функцией случайной величины t, как известно является

(x) еixt f (t)dt ,

где x - вспомогательный действительный параметр, представляющий собой интегральное преобразование Фурье от функции f(t).

Поскольку t – величина принципиально положительная, то


		(x) еixt f (t)dt ,
			0
а так как	f (t) е t ,
то
				е ( ix)t
(x)	еixt е t dt		е ( ix)t dt	( ix)
		0		( ix)
		0

(5.7)

		. (5.8)
	ix

С помощью характеристической функции легко определяется распределение композиции случайных величин.

Известно, что если

		k 1
	U (t) f j (t) ,
		j 1
то
			k 1
(U ) (x) xj (t) .
			j 1
В таком случае
		(x) (			)k 1 .	(5.9)
	(U )
			ix


Характеристическая функция однозначно определяет дифференци-
альную функцию распределения f(k ) (t)				искомой композиции.

Заменяя в уравнении ix на комплексный параметр – Р, можно полу-

чить

123


(U ) (x) е pt f(k ) (t)dt .	(5.10)
0
Если правую и левую части этого уравнения умножить на Р и под-

ставить значение (U ) (x) по уравнению (5.9), то можно получить интегральное уравнение ЛапласаКарсона


P(				)k 1		P		е Pt fk	(t)dt


			Р				0		.
							0
Решением этого уравнения является
fk (t) k 1							t(k 1) 1		е t
fk (t) k 1							(k 1) 1 !		е t
							(k 1) 1 !
или
	f		(t)		( t)k
	f	k	(t)				k!	е t
		k						.	(5.11)
								.	(5.11)

Полученное соотношение fk(t) соответствует закону Эрланга k-го по-

рядка.

Числовые характеристики этого распределения найти следующим образом.

По теореме сложения математических ожиданий

k 1

M k M i (k 1)M ,

i 1

где М – математическое ожидание промежутков ti с показательным распределением.

В свою очередь

							1
M t f (t)dt tе t dt							1
M t f (t)dt tе t dt							,
0				0			,
0				0
тогда
M			k 1	.			(5.12)
M	k			.			(5.12)
	k

Плотность потока Эрланга равна
			1			.	(5.13)
						.	(5.13)
k		M k			k 1
		M k			k 1
Аналогично по теореме сложения дисперсий
		k 1
Dk Di				(k 1)D ,

i 1

где D – дисперсия промежутков ti с распределением по показательному закону.

тогда

124

	D		k 1	.					(5.14)
	D			.					(5.14)
	k		2
			2
Использование закона Эрланга (5.11) затруднено тем, что по экспе-
риментальным данным можно найти k , а не λ.
Зная зависимость между ними (5.13), можно найти
~	k (k 1)				k	e	k (k 1)t	,	(5.15)
fok (t)	k!	k (k 1)t				e		,	(5.15)

где fok (t) - плотность нормированного по k закона Эрланга.

Численное значение k можно определить на основании экспериментальных значений k и Dk.

В самом деле из уравнения (5.13)

k (k 1) ,

подставляя λ в уравнение (5.14) можно получить
Dk		k 1				1		,

	2	(k 1)2			2 (k		1)
	2	(k 1)2			2 (k		1)
	k					k
в таком случае
	D 2		(k 1) 1
	k k
или
		k		1		1 .		(5.16)

			D		2
			D
			k		k

При подсчете по этой формуле k может оказаться дробным.

Для вычисления k! в уравнении (5.15) в этом случае удобней использовать равное ему значение гамма-функции Г(k+1).

Уравнение (5.15) примет тогда вид

fok (t)	k (k 1)	k	e	k (k 1)t	,	(5.17)
	(k 1)	k (k 1) t

который полностью соответствует плотности известного гаммараспределения.

5.4.Частные случаи распределения семян в рядке

исвязь гамма-распределения с другими

Уравнение распределения семян при посеве (5.15), (5.17) содержит два параметра k и k.

Как уже было отмечено, k - средняя плотность семян при посеве, зависящая от нормы высева, диктуется агротехническими соображениями и хозяйственно-экономическими условиями.

Среднее расстояние между семенами равно M 1 ,

		k	k
			k
а, в свою очередь,	1	.
а, в свою очередь,		.
k	M k
	M k

Влияние параметра k на распределение семян гораздо значительней.

125

При k = 0 распределения (5.15) и (5.17) примут вид:
~		(t) е k t	,
f	ok
		k

т.е. показательное распределение с дисперсией Dk 1 .

При k → ∞ значение дисперсии

Dk		1		0 .

	2	(k
	2	(k	1)
	k

Таким образом при k → ∞ уравнения (5.15) и (5.17) опишут регулярный поток событий с нулевой дисперсией.

Разумеется, что значение k = ∞, - практически невозможное событие, и для практических целей гораздо важнее знать как будет изменяться распределение семян и его числовые характеристики при больших, но все же ограниченных значениях k.

О виде распределения, как известно, можно судить по таким характеристикам, как показатель ассиметрии Sk

					S			3	,
					S	k			,
						k	3
							3
и эксцесса E			4	3 ,
и эксцесса E	k			3 ,
	k	4
		4
где 3 и 4 –соответственно,					третий и четвертый центральные моменты
распределения,
ζ – среднеквадратическое отклонение.
Для определения 3 и 4					можно вновь воспользоваться значением ха-
рактеристической функции гамма-распределения.
Начальные моменты mr (r = 1,2…) в этом случае определяют просто
				m	i	r (r)				(0) ,
				r				U ( x)

т.е. необходимо найти r-тую производную характеристической функции по x и приравнять x нулю.

По формуле (5.9)

	(		)k 1 .
u( x)
		ix

Первый начальный момент

m1 i 1 u' (x) при х = 0.

После подстановки u(x) и незначительных преобразований получа-

ется

m1 k 1 .

Соответственно, второй, третий и четвертый моменты равны:

m	(k 1)(k 2)	;	m	(k 1)(k 2)(k 3)	;

2	2		3	3

126

m	(k 1)(k 2)(k 3)(k 4)				.
m					.
4				4
				4
Для перехода от начальных моментов к центральным пользуются
формулами
			1 0
		2	m m2
		2	2	1

3 m3 3m1m2 2m13

4 m4 4m3m1 6m2m12 3m14

После подстановки значений mi центральные моменты оказываются равными, соответственно,

	(k 1)	;		2(k 1)	;		3(k 1)(k 3)	;	(5.18)
2	2		3	3		4	4

С учетом этих значений i и того, что λ = k(k+1) коэффициент асимметрии будет равен

				2 3
		M	3	2 3	(k 1) k 1		2
S			3	k				,
	k	3		3		(k 1)2
							k 1


					k
а эксцесс

		M	4	3	3 4	(k 1)3 (k 3)		3	3(k 3)	3.
Е			4		k
Е	k	4				4	(k 1)4		(k 1)
	k

						k

Нетрудно заметить, что с ростом k, Sk и Ek будут стремиться к нулю. Если учесть дополнительно, что вычисление высших моментов на

основе экспериментальных данных связано с большими ошибками, то можно считать, что значения k в нескольких десятков единиц приводят Sk и Ek к несущественным величинам. Но равенство Sk и Ek нулю характерно лишь для нормального закона распределения.

Таким образом, при возрастании k распределение семян в рядке стремится к нормальному, которое таким образом можно считать частным случаем распределения семян.

При постоянном значении λ возрастание k связано с ростом Мk (5.12), так что увеличение среднего расстояния между семенами приближает распределение к нормальному.

В свою очередь, Т. Саати [5.31], А. Кофман, Р. Крюон [5.4] называют гамма-распределение частным случаем распределения Пирсона III-го рода.

Действительно, распределение Персона III-го рода, согласно Л.К. Лахтину [5.33], имеет вид:

y y0 e x (1 x)m ,

где	y		N m 1	m e	,	(5.19)
где	y	0	Г (m 1)		,	(5.19)
		0

N – количество проведенных опытов; γ, m – параметры распределения;

127

ℓ - среднее значение; x – текущий параметр.

Управление написано для начала координат в точке х = ℓ .

Перенеся координаты в начало кривой распределения (как это сдела-

но для уравнений 5.15 и 5.17), можно получить

х =-ℓ + х1,

где х1 – новый текущий параметр.

Уравнение (5.19) примет в этом случае вид

	е	x	m
y y0	е		x	,
где

N m 1

Г (m 1)

Если параметром γ и m придать соответствующие значения

k (k 1)

m k ,

то можно найти

N k (k 1) k 1

k (k 1) x

Г(k 1)

N k (k 1)

k (k 1) x

(k 1)x

Г(k 1)

Сравнив этот результат с формулой (5.17), можно сделать вывод об их полном сходстве.

Результаты данного анализа позволяют объяснить широкое разнообразие мнений о виде закона распределения семян [5.34].

5.5.Экспериментальная проверка применимости гамма-распределения

кописанию распределения семени при пунктирном посеве

5.5.1. Методика проведения эксперимента

Проверку распределения семян проводят обычно в лабораторных и полевых условиях.

В лабораториях эксперименты проводят обычно на установках с клейкой лентой или в почвенном канале.

Лабораторные опыты более сопоставимы, на них легче определять влияние тех или иных факторов и устанавливать определенные закономерности.

Недостатком известных лабораторных устройств исследования сеялок является ограниченность числа наблюдений (особенно это касается почвенного канала) и отсутствие воздействий на аппарат ряда факторов внешней среды (неровностей поля, твердость почвы и т.д.).

Результатам полевых опытов доверяют гораздо больше, но и в этом случае необходимо видеть крупные недостатки, связанные с той же ограниченностью количества измерений и их полной невоспроизводимостью.

128

Очень важным, с методологической точки зрения, является вопрос о количестве измерений, представляющих репрезентативную выборку.

Сложность решения этой задачи вызывает то обстоятельство, что практически все существующие рекомендации по выбору числа наблюдений гарантируют лишь определенную точность в оценке математического ожидания изучаемой величины. Но равномерность размещения зависит от дисперсии.

Построение доверительного интервала для дисперсии, как правило, основано на использовании 2 – распределения (распределения Пирсона), но, строго говоря, этот метод совершенно точен, если изучаемые величины имеют нормальное распределение вероятностей.

В работе [5.35] удалось доказать, что среди оценок, характеризую-

щих гамма-распределение, DK и k являются оценками максимального

правдоподобия. Известно также, что оценки максимального правдоподобия имеют нормальное распределение.

Доверительный интервал для дисперсии в этом случае строят [5.30] по уравнению:

I (Dk~ ) (Dk	t (Dk~ ) ;	Dk t (Dk~ ) )	,	(5.20)
~		~
где ( D~ ) - среднеквадратическое		отклонение распределения		дисперсии,
k

вычисляемой по результатам выборочного наблюдения.

Дисперсия дисперсии выборочной величины t определяется согласно А.Хальду [5.36] и Е.С. Вентцель [5.30] формулой:

D(Dk )	1	4	n 3	2
D(Dk )		4		Dk	.
~	n		п(п 1)
	n		п(п 1)

Значения второго и четвертого центральных моментов уже определе-

ны (5.18)

k 1

;

3(k 1)(k 3)

Кроме этого, в целях упрощения расчетов отношение

n 3

1, так

n 1

как число измерений определяется многими сотнями, тысячами.

В этом случае

D( Dk )

(

4 2 ) ,

3(k 1)(k 3)

(k 1)4

( Dk )

После некоторых преобразований можно получить

D( Dk )

2(k 1)(k 4)

n 4

и, соответственно,

2(k 1)(k 4)

( Dk )

D( Dk~ )

(5.21)

129

Когда значение ~ найдено, то доверительный интервал для дис-

( Dk )

персии может быть построен по уравнению (5.20), где величину tβ в зависимости от принятой доверительной вероятности β и числа степеней свободы k = n-1, по таблицам tβ – распределения [5.30].

Уравнение (5.21) можно использовать и для обоснования числа необходимых замеров, при которых относительная ошибка в определении дисперсии ε не превысит заданный уровень.

Относительная ошибка ε может быть выбрана равной, например 0,025; 0,05; 0,075; 0,1, что соответствует определению дисперсии с точно-

стью до 2,5…10%.

Доверительный интервал I (Dk~ ) тогда может быть представлен как

I (D~ ) 2 Dk .

В таком случае из уравнения (5.20) следует, что

( D )

I ( D )

После подстановки этого значения в формулу (5.21) и некоторых

преобразований можно получить

2(k 1)(k 4)

8t 2 (k 1)(k 4)

2 ~

(Dk )

D( Dk )

I ( Dk)

Если вместо λ подставить равное ему значение (5.13)

(k 1) , где

, то

M k

2 (k 4)

I 2

(k 1)3

( Dk)

По этой формуле можно оценить порядок величины n, подставляя в нее типичные значения входящих параметров.

Пример.

Пусть среднее расстояние между семенами Мk = 4 см, коэффициент вариации V = 60%, доверительная вероятность β = 0,95. Требуется определить, при каком количестве измерений дисперсия Dk может быть определена с относительной ошибкой, не превышающей ε = 0,05 (т.е. 5%).

Расчет осуществляется достаточно просто:

						1		1	0,25 ;						V Vk		60 4		2,4 см.
									0,25 ;				k						2,4 см.
				k		M k	4						k	100		100
						M k	4							100		100
	D 2				2,42		5,76см2 ;					k		1		1			1	1	1,77


		k		k										D 2				5,76 0,252
														D 2				5,76 0,252
				1,96, 82 ;										k k
t		t	95	1,96, 82 ;					I	(	D~	) 2 D				2 0,05 5,76 0,575см2
			95								D~				k
											k

130

n			8t 2 (k 4)			8 1,962 (1,77 4)					6448 .
n	I	2		4	3	0,576	2	0,25	2	(1,77 1)	6448 .
	I		( Dk)	(k 1)		0,576		0,25		(1,77 1)
			( Dk)	k

Результаты расчета для других значений коэффициента вариации и желаемой точности в определении дисперсии приведены в табл.5.2.

Таблица 5.2

Количество измерений, необходимых для оценки дисперсий

сопределенной относительной точностью при шаге посева Mk = 4 см

идоверительной вероятности β = 0,95

Желательная	Возможные оценки равномерности распределения семян
точность в
определении	V=20%	V=40%	V=60%	V=80%	V=100%
дисперсии,	D=0,64см2	D=2,65см2	D=5,76см2	D=10,24см2	D=16см2
%
2,5	13790	18220	25700	36026	49113
5,0	3442	4560	6448	9220	12278
7,5	1532	2021	2860	4339	5457
10,0	862	1141	1612	2450	3070
12,5	552	729	1031	1561	1965
15,0	383	506	715	1086	1364

Из данных таблицы 5.2 следует, что для повышения точности в определении статистической дисперсии требуется существенное увеличение числа измерений.

Устройство для автоматического анализа равномерности высева семян

Проведение массовых наблюдений расстояний между семенами возможно лишь при наличии приборов, позволяющих иметь достаточно большой объем непрерывной записи и автоматическую обработку результатов.

Известно большое количество работ, направленных на создание таких устройств. При этом в качестве датчиков импульсов от пролетающих семян были использованы пьезодатчики, фотоэлементы и фотодиоды, емкостные и индуктивные преобразователи. К сожалению, с помощью этих устройств удавалось фиксировать лишь время между выходом семян из высевающего аппарата. Различие в траекториях падающих семян они не отражали и, тем самым, вносили существенное искажение в характеристики различных распределений.

Для устранения этого недостатка была разработана аппаратура, позволяющая учитывать как временную, так и пространственную сторону этого технологического процесса [5.37].

Достигается это тем, что искусственная поверхность для высева выполнена в виде блока пьезодатчиков, преобразующих механические им-

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 1213 / 2213 14 15 16 17 18 19 20 21 22 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
09.01.20246.75 Mб1858.pdf
#
09.01.20246.76 Mб0859.pdf
#
09.01.2024449.76 Кб086.pdf
#
09.01.20246.83 Mб0860.pdf
#
09.01.20246.88 Mб2861.pdf
#
09.01.20246.93 Mб2862.pdf
#
09.01.20247.06 Mб0863.pdf
#
09.01.20247.07 Mб0864.pdf
#
09.01.20247.21 Mб1865.pdf
#
09.01.20247.21 Mб0866.pdf
#
09.01.20247.3 Mб0867.pdf