Метод узловых напряжений

Метод основан на применении первого закона Кирхгофа. Составляется уравнение для потенциалов узлов схемы, при условии, что потенциал одного из узлов принят равным нулю. После того как найдены потенциалы узлов, находят токи в ветвях по закону Ома.

При составлении уравнений следует пользоваться следующими правилами:

1. В левой части уравнения записывают произведение потенциала рассматриваемого узла, умноженного на сумму проводимостей ветвей, примыкающих к этому узлу, а вычитают произведения, учитывающие связи соседних узлов, в которых потенциал соседнего узла умножается на суммарную проводимость ветвей связи.

2. Правая часть уравнений представляет собой алгебраическую сумму произведений ЭДС на соответствующие проводимости тех ветвей, которые присоединены к рассматриваемому узлу. Это произведение берется с положительным знаком, если ЭДС направлена к узлу.

3. Если ветвь содержит источник тока, и он направлен к узлу, то в правой части уравнения его учитывают со знаком плюс.

Рассмотрим принцип составления уравнений методом узловых напряжений.

Для данной схемы необходимо составить систему из трех уравнений для узлов 1,2,3. Потенциал четвертого узла равен нулю. Тогда с учетом сформулированных правил получим:

Здесь G₁= 1/R₁; G₂= 1/R₂; G₃= 1/R₃; G₄= 1/R₄; G₅= 1/R₅.

После нахождения потенциалов, ищем токи в ветвях, предварительно указав на схеме выбранные направления токов.

; ;;;

.

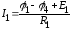Метод наложения

При действии нескольких источников напряжения и токов в линейной электрической цепи неизвестные токи в ветвях такой цепи можно найти суммированием токов от каждого источника в отдельности. При этом, исключенные из схемы источники заменяют их внутренними сопротивлениями, закорачивая источники ЭДС и размыкая источники тока. Рассмотрим электрическую цепь. Пользуясь методом наложения, определим токи в ветвях схемы.

R3 E1 J2 R2 R1 I1 I3 I2

E1 R1 R2 R3 R1 1 2

R2 R3 J2 1 2

Исключив из схемы источник тока J₂ , найдем частичные токи в ветвях под воздействием источника ЭДС E₁.

; .

Теперь исключим из схемы источник E₁ и найдем частичные токи в ветвях от воздействия источника тока J₂. Согласно первому закону Кирхгофа имеем: , тогда положив,можем записать:

.

; ;.

Истинные значения токов в ветвях найдем из соответствующих сумм частных токов:

; ;.

Рассмотренный метод, однако, не применим при вычислении мощностей, так как мощность есть квадратичная функция тока или напряжения.

Свойство взаимности

Если в ветвь «n» электрической цепи включить единственный источник ЭДС E_n, то в ветви «m» он создаст ток I_m и тот же источник ЭДС E_m = E_n, включенный в ветвь «m», создаст в ветви «n» ток I_n = I_m.

Или иначе:

Взаимная проводимость двух любых ветвей определяется отношением тока в одной ветви к ЭДС в другой при равных нулю ЭДС в остальных ветвях, а взаимное сопротивление двух ветвей обратно взаимной проводимости тех же ветвей.

Рассмотрим электрическую цепь:

Преобразуем схему к виду:

Следующее преобразование схемы имеет вид:

Наконец последнее преобразование схемы дает:

; ; .

.

Принцип взаимности был установлен Кирхгофом. Обычно этот метод эффективен при расчете цепей с ограниченном числом источников.