Действующее значение и мощность при несинусоидальных напряжениях и токах

Действующее значение несинусоидального тока определяется, как и для синусоидального тока, по равенству средней мощности перемен­ного тока и мощности постоянного тока в том же сопротивлении r.

,

т. е. действующее значение периодического переменного тока

является его среднеквадратичным значением за период. После подстановки в это выражение тока i в виде ряда Фурье:

Следовательно,

т. е. действующее значение тока равно корню квадратному из суммы квадратов постоянной составляющей и действующих значений токов всех гармоник, и не зависит от их начальных фаз.

По аналогии действующее значение напряжения .

Важной характеристикой кривой является среднее значение ее абсолютной величины за период

.

Например, для синусоиды

.

Для характеристики кривых без постоянной составляющей пользуются несколькими коэффициентами.

Коэффициент иска­жения равен отношению действующего значения первой гармоники к действующему значению всей кривой: ; в случае синусоиды.

Коэффициент амплитуды равен отно­шению максимального значения U_m к действующему U: ; для синусоиды .

Коэффициент формы равен отношению действующего значения U к среднему значению кривой: ; для синусоиды.

Мгновенная мощность р после разложения напряжения и тока в ряды Фурье получает вид:

,

т.е., кривая мгновенной мощности имеет весьма сложную форму, но средняя мощность равна сумме средних мощностей, создаваемых одноименными гармониками напряжения и тока:

.

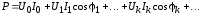Расчет линейных цепей при несинусоидальных напряжениях и токах

Если напряжение, приложенное к цепи, имеет сложную форму:

,

то ток цепи с активным сопротивлением

,

ток в цепи с индуктивностью L

,

ток цепи с емкостью С

.

Отсюда видно, что каждой гармонике напряжения соответствует своя гармоника тока, вычисляемая независимо от других гармоник.

При пренебрежении поверхностным эффектом активное сопротивление для всех гармоник одинаково. Индуктивное сопротивление растет, а емкостное-убывает пропорционально порядку гармоники.

Таким образом, для расчета сложных линейных цепей может быть применен метод наложения: после разложения кривых заданных напряжений и токов в ряд Фурье задача решается для каждой гармоники в отдельности; при этом сопротивления ветвей для каждой гармоники в общем случае будут различными. Задачи для отдельных гармоник решаются однотипно и при их решении может быть использован весь аппарат теории синусоидальных токов – векторные диаграммы, символический метод и т. д. Затем можно произвести наложение решений для мгновенных значений отдельных гармоник – напряжений и токов каждой ветви и вычислить их действующие значения и мощность.