Определение параметров четырехполюсника

Если известны конкретная схема и сопротивления (проводимости) ветвей четырехполюсника, то его параметры могут быть определены расчетным путем по входным и взаимным проводимостям. Можно также исходить непосредственно из зависимостей, устанавливаемых зако­нами Кирхгофа.

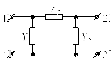
В качестве примера рассмотрим простейшие схемы четы­рехполюсников. Так как из четырех параметров четырехполюсника независимыми являются три, то простейшие схемы должны содержать три ветви, т. е. представлять собой соединение звездой (Т-образная схема) или треугольником (П-образная схема).

Для Т-образной схемы при режиме холостого хода очевидны следующие соотношения:

, ;

при коротком замыкании:

,

Отсюда параметры этого четырехполюсника:

, ,,

Параметры П-образной схемы могут быть определены аналогич­но:

при холостом ходе:

, ;

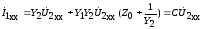при коротком замыкании

,

Отсюда параметры П-схемы

, ,,

Любой сложный четырех­полюсник можно заменить простейшим эквивалентным ему, т. е. Т- или П-схемой. Параметры этих эквивалентных схем выражаются через параметры четырехполюсника.

Для Т-схемы: ,,;

Для П-схемы: ,,.

Из этих выражений видно, что схемы, эквивалентные симметрич­ным четырехполюсникам, сами тоже симметричны, так как, если , то и.

Если конкретная схема и параметры ветвей четырехполюсника неизвестны, его параметры могут быть определены из опытов холостого хода и короткого замыкания при питании и измерениях со стороны входа и со стороны выхода. Эти измерения позволяют опре­делить комплексы сопротивлений короткого замыкания и холо­стого ходапри питании схемы со стороны входных зажимов 1'-1″ иипри питании схемы со стороны выходных зажимов 2' -2":

; ;

; ;

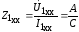Как видно из этих выражений, полные сопротивления при корот­ком замыкании и холостом ходе связаны между собой соотношением:

,

поэтому из четырех вышеупомянутых опытов необходимы лишь три, а четвертый может служить для контроля.

Параметры четырехполюсника находят по формулам:

; ;;.

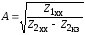Периодические несинусоидальные напряжения и токи в линейных цепях Разложение периодических функций в ряд Фурье

До сих пор рассматривались линейные цепи при постоянных и синусоидальных напряжениях и токах. Синусоидальная форма кривых позволила применить векторные диаграммы и символический метод, весьма упростившие расчет цепей.

В электротехнике стремятся к синусоидальной форме периодических кривых, так как большинство устройств при этом работает лучше, однако на практике кривые несколько отличаются от синусоид. Более того, в устройствах электронной и вычислительной техники часто напряжения и токи должны быть несинусоидальными. В этих случаях можно использовать рассмотренные ранее методы расчета цепей, если разложить периодические несинусоидальные кривые в ряд Фурье.

Как известно из математики, периодическая функция , удовлетворяющая условиям Дирихле, может быть приближенно представлена тригонометрическим рядом. Этот ряд состоит из суммы постоянной составляющейА₀ и синусоид разных частот , гдеk – целые числа, начиная с единицы, :

.

Причем член называют постоянной составляющей, член, имеющей частоту, равную частоте данной функции, называют основной или первой гармоникой, а все остальные члены виданосят название высших гармоник.

Ряд Фурье может быть записан в другой форме, если развернуть синусы сумм:

,

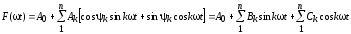где и,

т.е. ,.

Коэффициенты ряда необходимо вычислять следующим образом:

, и.

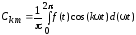Постоянная составляющая ряда является, очевидно, средним значением функции за период.

Часто периодическая функция, подлежащая разложению в ряд Фурье, задается не аналитическим выражением, а в виде графика. В этом случае разложение в ряд можно выпол­нить приближенно, заменив интегрирование суммированием подын­тегральных выражений для конечного числа ординат кривой . Дляп равноотстоящих друг от друга на ординат следует подставитьвместо.

Тогда . Аналогично ,