
- •Тема № 13. Гироскопические приборы и устройства
- •Основные понятия
- •Гироскоп с тремя степенями свободы
- •1. Поворотное (кориолисово) ускорение
- •2. Гироскопический момент
- •3. Движение гироскопа под действием внешних сил
- •Роторные вибрационные гироскопы роторные вибрационные гироскопы
- •4. Гироскоп с внутренним кардановым подвесом
- •1. Погрешности гироскопа, методы их компенсации.
- •1.1. Кажущееся движение гироскопа
- •2. Системы коррекции.
- •2.1. Необходимость коррекции в гироскопическихприборах.
- •3. Гироскопические вертикали
- •2. Авиагоризонт бомбардировщика агб-3
- •Основные проверяемые характеристики
- •Основные технические данные агд-1
- •Гировертикали с силовой гироскопической стабилизацией
- •1. Свойства гироскопа с двумя степенями свободы
- •2. Гироприборы на основе двухстепенного гироскопа
- •Вставить
- •Выключатель коррекции вк-90
- •Основные технические данные выключателя коррекции вк-90
- •3. Особенности эксплуатации гироскопических устройств
2. Гироскопический момент
Предположим,
что ротор гироскопа, вращаясь вокруг
главной оси XX
с угловой скоростью
![]() ,
поворачивается вокруг оси УУ с угловой
скоростью
,
поворачивается вокруг оси УУ с угловой
скоростью![]() (рис. 3.). Причем
(рис. 3.). Причем![]() значительно больше
значительно больше![]() .
.
Рассмотрим
на роторе симметрично расположенные
четыре материальные точки
![]() ,
,![]() ,
,![]() и
и![]() ,.
Все эти четыре материальные точки будут
участвовать в сложном движении и будут
иметь поворотные ускорения. Определим
направления этих ускорений в каждой
точке в отдельности.
,.
Все эти четыре материальные точки будут
участвовать в сложном движении и будут
иметь поворотные ускорения. Определим
направления этих ускорений в каждой
точке в отдельности.
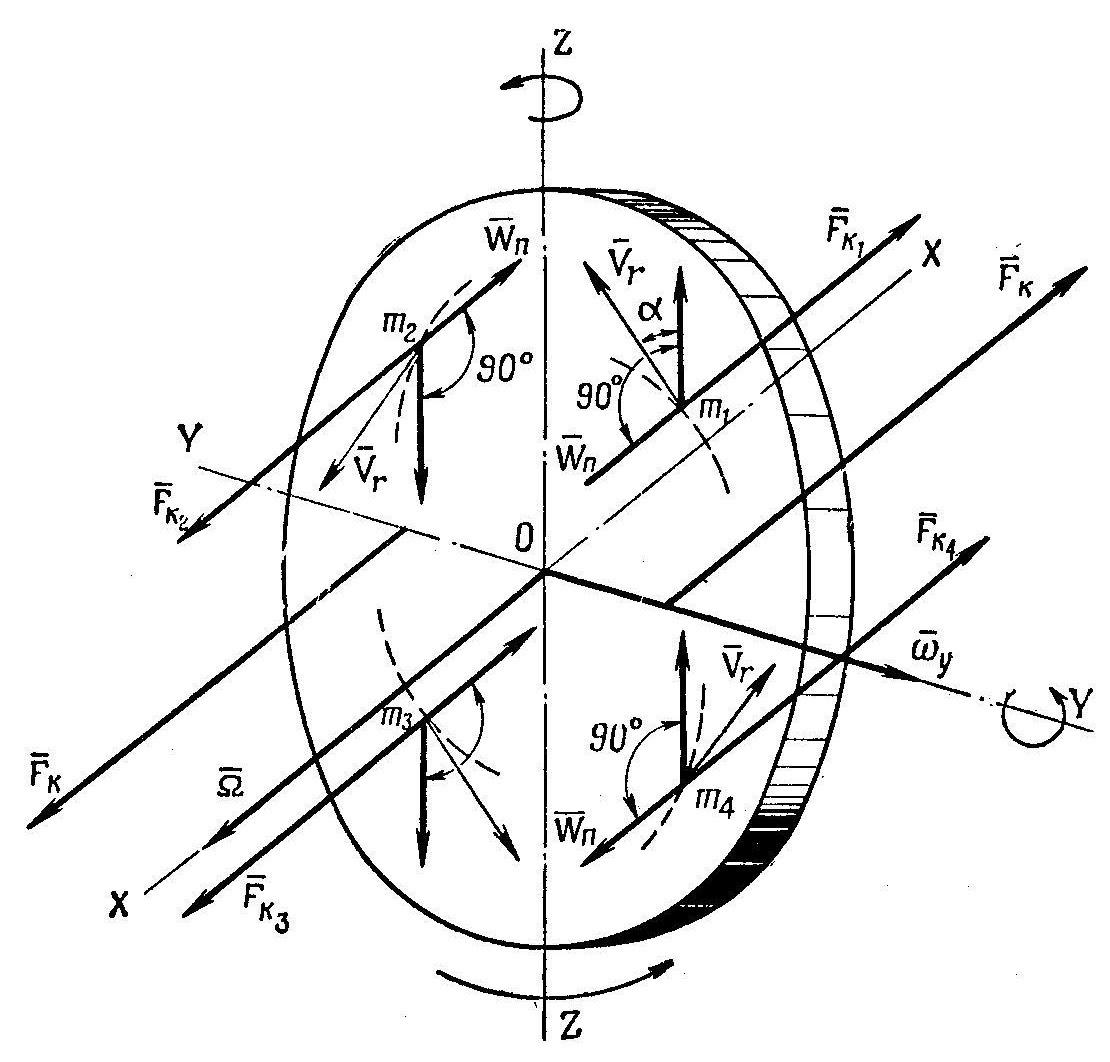
рис.3
Точка
![]() совершает относительное вращательное
движение вокруг осиXX.
Вектор относительной скорости
совершает относительное вращательное
движение вокруг осиXX.
Вектор относительной скорости
![]() направлен по касательной к траектории
движения точки
направлен по касательной к траектории
движения точки
![]() .
Так как вектор
.
Так как вектор
![]() не перпендикулярен оси УУ (оси переносного
движения), в создании поворотного
ускорения будет участвовать та
составляющая скорости, которая
перпендикулярна оси УУ. Из рис. 3, видно,
что эта часть скорости равна
не перпендикулярен оси УУ (оси переносного
движения), в создании поворотного
ускорения будет участвовать та
составляющая скорости, которая
перпендикулярна оси УУ. Из рис. 3, видно,
что эта часть скорости равна
;
V=V![]() cos
cos![]() .
.
Для
определения направления поворотного
ускорения
![]() необходимо повернуть векторV
на угол 90° в направлении переносного
движения. Очевидно, направление
поворотного ускорения
необходимо повернуть векторV
на угол 90° в направлении переносного
движения. Очевидно, направление
поворотного ускорения
![]() будет перпендикулярно плоскости ротора
и совпадет по направлению с вектором
угловой скорости относительного
вращательного движения
будет перпендикулярно плоскости ротора
и совпадет по направлению с вектором
угловой скорости относительного
вращательного движения![]() .
.
Рассуждая подобным образом, нетрудно определить:
а) что
поворотные ускорения точек
![]() и
и![]() направлены в сторону, противоположную
направлению вектора
направлены в сторону, противоположную
направлению вектора![]() .
.
б) что
поворотное ускорение точки
![]() направлено по направлению вектора
направлено по направлению вектора![]() .
.
Инерционные
силы Кориолиса
![]() ,
,![]() ,
,![]() и
и![]() этих точек направлены в стороны,
противоположные поворотным ускорениям.
Такие же инерционные силы вызываются
и всеми остальными материальными точками
тела. Каждая материальная точка правой
части ротора будет находиться под
воздействием инерционной силы определенной
величины, которая направлена в сторону,
противоположную направлению вектора
этих точек направлены в стороны,
противоположные поворотным ускорениям.
Такие же инерционные силы вызываются
и всеми остальными материальными точками
тела. Каждая материальная точка правой
части ротора будет находиться под
воздействием инерционной силы определенной
величины, которая направлена в сторону,
противоположную направлению вектора![]() .
Направление инерционных сил, действующих
на материальные точки левой части
ротора, будет совпадать с направлением
вектора
.
Направление инерционных сил, действующих
на материальные точки левой части
ротора, будет совпадать с направлением
вектора![]() .
.
Результирующие
инерционных сил Кориолиса
![]() правой и левой части ротора будут
создавать пару сил относительно осиZZ.Под
действием этой пары сил возникнет
реактивный момент
правой и левой части ротора будут
создавать пару сил относительно осиZZ.Под
действием этой пары сил возникнет
реактивный момент
![]() ,
действующий вокруг осиZZ
и стремящийся повернуть ось XX
собственного вращения гироcкопа
к оси УУ вынужденного вращения. Реактивный
момент этой пары сил
,
действующий вокруг осиZZ
и стремящийся повернуть ось XX
собственного вращения гироcкопа
к оси УУ вынужденного вращения. Реактивный
момент этой пары сил
![]() называется гироскопическим моментом.
Аналогично можно доказать, что если
гироскоп, вращающийся вокруг осиXX,
поворачивать вокруг оси ZZ,
то появится гироскопический момент М
называется гироскопическим моментом.
Аналогично можно доказать, что если
гироскоп, вращающийся вокруг осиXX,
поворачивать вокруг оси ZZ,
то появится гироскопический момент М![]() .
вызывающий вращение гироскопа вокруг
оси УУ. Для определения направления
гироскопического момента существует
несколько правил. Наиболее часто
пользуются правилом профессора Н.Е.
Жуковского.
Правило профессора Н. Е. Жуковского:
если гироскоп, вращающийся вокруг
собственной оси, поворачивать вокруг
другой оси, то возникает гироскопический
момент, стремящийся совместить по
кратчайшему пути угловую скорость
собственного вращения с угловой скоростью
вынужденного вращения.
.
вызывающий вращение гироскопа вокруг
оси УУ. Для определения направления
гироскопического момента существует
несколько правил. Наиболее часто
пользуются правилом профессора Н.Е.
Жуковского.
Правило профессора Н. Е. Жуковского:
если гироскоп, вращающийся вокруг
собственной оси, поворачивать вокруг
другой оси, то возникает гироскопический
момент, стремящийся совместить по
кратчайшему пути угловую скорость
собственного вращения с угловой скоростью
вынужденного вращения.
Для
вывода формулы значения гироскопического
момента возьмем гироскоп, ротор которого
имеет форму диска и вращается с угловой
скоростью
![]() .
вокруг собственной оси вращения XX
(рис.
4). Допустим, что мы пытаемся повернуть
ротор гироскопа относительно оси УУ
(оси внутренней рамки) с угловой скоростью
.
вокруг собственной оси вращения XX
(рис.
4). Допустим, что мы пытаемся повернуть
ротор гироскопа относительно оси УУ
(оси внутренней рамки) с угловой скоростью
![]() .
Выделим в теле ротора гироскопа
элементарный объем, образованный
сторонами dr,
dr
.
Выделим в теле ротора гироскопа
элементарный объем, образованный
сторонами dr,
dr![]() и b.
Определим действующую на этот элементарный
объем инерционную силу Кориолиса
и b.
Определим действующую на этот элементарный
объем инерционную силу Кориолиса
![]() Она
| равна произведению поворотного
ускорения
Она
| равна произведению поворотного
ускорения
![]() на массу выделенного элементарного
объемаdт:
на массу выделенного элементарного
объемаdт:
![]() =
=![]() dт.
dт.
Масса элементарного объема равна
dт=
![]() rd
rd![]() drb,
drb,
где
![]() -
массовая плотность материала ротора.
-
массовая плотность материала ротора.
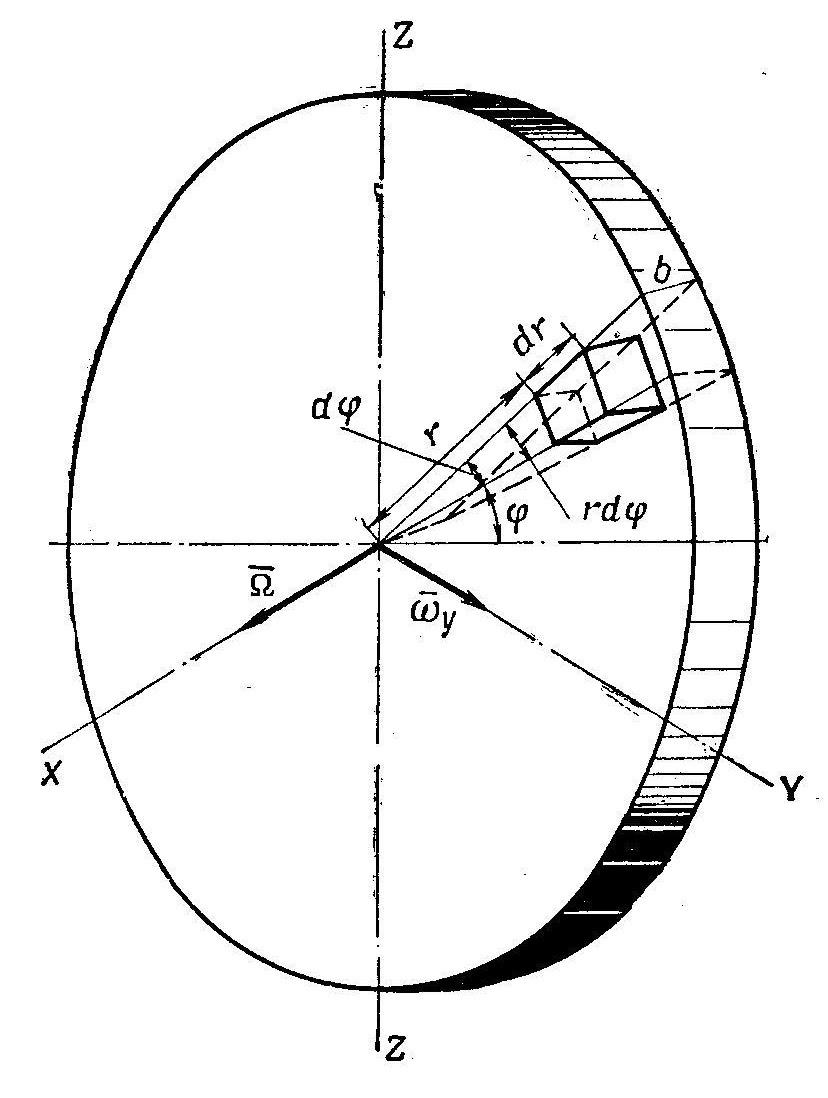
рис.4
Значение
поворотного ускорения
![]() находим из выражения
находим из выражения
![]() =2
=2![]() cos
cos![]() =2
=2![]()
Тогда
![]() =
=![]()
Элементарный
гироскопический момент
![]() ,
развиваемый инерционной силой
,
развиваемый инерционной силой![]() относительно оси
ZZ,
будет равен произведению этой силы на
расстояние от точки ее приложения до
оси
ZZ
(на
расстояние, равное rcos
относительно оси
ZZ,
будет равен произведению этой силы на
расстояние от точки ее приложения до
оси
ZZ
(на
расстояние, равное rcos![]() ),
т. е.
),
т. е.
![]() .
.
Для
получения значения полного гироскопического
момента М![]() проинтегрируем полученное выражение
при изменении r
от 0 до R
и
проинтегрируем полученное выражение
при изменении r
от 0 до R
и
![]() от
от![]() до
+
до
+![]() (гдеК—радиус
ротора гироскопа):
(гдеК—радиус
ротора гироскопа):
М![]() =
2
=
2![]() b
b![]() r
r![]() dr
dr![]() cos
cos![]()
![]() d
d![]() = =2
= =2![]() b|
b|![]() /4||
/4||![]() |
|![]() /2
+ 1/4sin2
/2
+ 1/4sin2![]() ||
||![]()
Подставив пределы интегрирования, получим
М![]() =
2
=
2![]()
![]() b
R
b
R![]()
![]() /4
=
/4
=
![]() R
R![]() b
R
b
R![]() /2
/2
![]()
В этом
выражении
![]() R
R![]() b
=т—масса
ротора, а выражение
b
=т—масса
ротора, а выражение
M
R![]() /2
=
j
— момент инерции ротора гироскопа
относительно оси его симметрии.
/2
=
j
— момент инерции ротора гироскопа
относительно оси его симметрии.
Таким образом, окончательно будем иметь
М![]() = J
= J![]()
![]() (13.1)
(13.1)
Тогда выражение (13.1) принимает вид
M![]() = H
= H![]() (13.2)
(13.2)
Величину
J![]() =
Н
в технике называют кинетическим моментом
гироскопа, а в прикладной теории
гироскопов —собственным моментом
гироскопа. Мы рассмотрели случай, когда
вынужденное вращение ротора гироскопа
происходило вокруг оси УУ. Если вынужденное
вращение ротора происходит вокруг оси
ZZ,
то возникает гироскопический момент
М
=
Н
в технике называют кинетическим моментом
гироскопа, а в прикладной теории
гироскопов —собственным моментом
гироскопа. Мы рассмотрели случай, когда
вынужденное вращение ротора гироскопа
происходило вокруг оси УУ. Если вынужденное
вращение ротора происходит вокруг оси
ZZ,
то возникает гироскопический момент
М![]() действующий относительно оси УУ.
Величина
действующий относительно оси УУ.
Величина
гироскопического
момента М![]() (аналогично рассмотренному выше) равна
(аналогично рассмотренному выше) равна
М![]() = H
= H![]()
Выражение
для гироскопического момента М![]() было выведено для частного случая, когда
угол между осями собственного и
вынужденного вращений гироскопа, т. е.
угол между векторами
было выведено для частного случая, когда
угол между осями собственного и
вынужденного вращений гироскопа, т. е.
угол между векторами
![]() и
и
![]() составлял 90°. В общем случае, когда этот
угол будет отличным от 90°, выражение
гироскопического момента несколько
изменится.
составлял 90°. В общем случае, когда этот
угол будет отличным от 90°, выражение
гироскопического момента несколько
изменится.
Представим
себе, что ротор гироскопа развернут
относительно оси УУ на угол (90°—![]() ).
Пусть ротор гироскопа вращается вокруг
).
Пусть ротор гироскопа вращается вокруг
собственной
оси вращения с постоянной угловой
скоростью
![]() и принудительно поворачивается вокруг
оси
2.2,
внешней рамки карданного подвеса с
угловой скоростью
и принудительно поворачивается вокруг
оси
2.2,
внешней рамки карданного подвеса с
угловой скоростью
![]() (рис.5 ). В этом случае угол между векторами
(рис.5 ). В этом случае угол между векторами![]() и
и![]() равен некоторому углу 5, а не 90°.
равен некоторому углу 5, а не 90°.
Нетрудно
убедиться, что в этом случае инерционная
сила F![]()
будет лежать в горизонтальной плоскости и составлять с плоскостью ротора такой же угол 5. Проекция этой силы на направление, перпендикулярное к плоскости вращения ротора, будет равна
F![]() cos
(90°—
cos
(90°—![]() )
=F
)
=F![]() sin
sin![]()
Подставляя это значение в выражение (13.2), получим
M![]() =
J
=
J![]() sin
sin![]() или
или
M![]() =
H
=
H![]() sin
sin![]() (13.3)
(13.3)
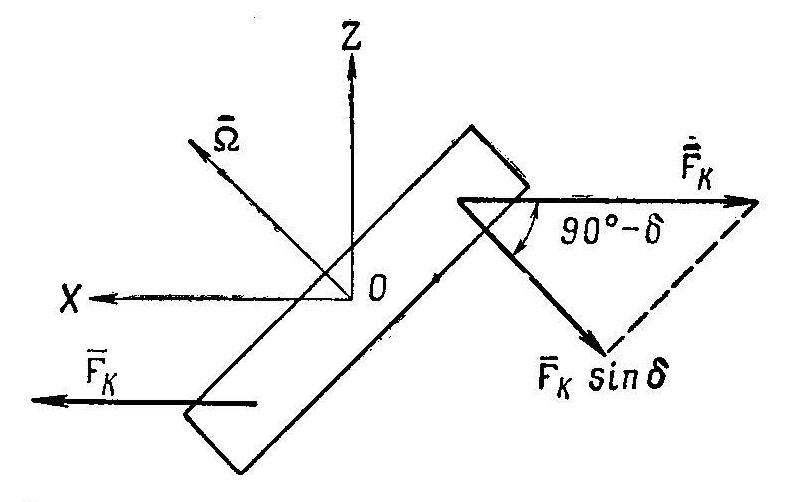
рис.5
Из
уравнения (13.3) видно, что если ось ротора
составляет c
вектором переносной угловой скорости
![]() угол
угол
![]() ,
то возникновение гироскопического
момента обусловлено только составляющей
угловой скорости
,
то возникновение гироскопического
момента обусловлено только составляющей
угловой скорости
![]() sin
sin![]() ,
перпендикулярной вектору кинетического
момента.
,
перпендикулярной вектору кинетического
момента.
