Метод формирования данных.

S_i – оценка показателя эффективности с точки зрения элементов.

d_i ≤ S_i ≤ D_i

d₁ = 1 d₂ = 4

D₁ = 3 D₂ = 8; S_i - ?

(2)

Целевая функция элемента будет иметь следующий вид:

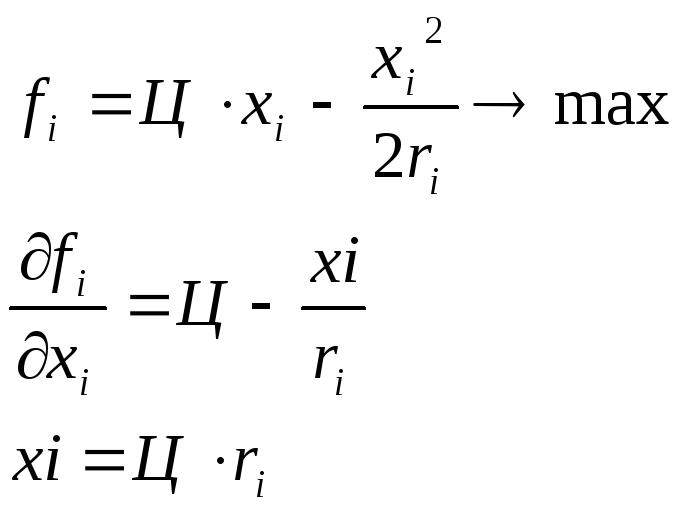
Задача: для рассмотренного выше примера определить оптимальные стратегии элементов S_i –? r₁ = 2, r₂ = 6, Ц = 15

Имея возможность своими сообщениями влиять на те решения, которые принимает центр элементы постараются сообщить такую информацию, чтобы было принято наиболее выгодное для них решение, т.е. та информация, которую сообщает элемент не обязательно будет достоверной. Этот эффект искажения информации называется эффектом манипулирования информацией.

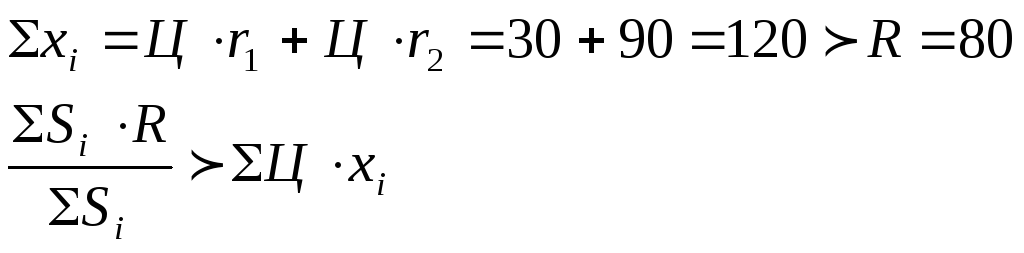
Обозначим через V- желаемый объем производства, а через R – требуемый. Рассмотрим 3 случая:

1. V=R, S_i^p =r_i

2. V>R, S_i^p = D_i

3) V<R, S_i^p = d_i.

Равновесное состояние (состояние Неша) – устойчивым исходом взаимодействия элементов можно считать такой вектор действий, от которого в одиночку никому не выгодно отклонятся. Это значит, что ни один из элементов в одиночку менять свою стратегию не может увеличить свой выигрыш при условии, что остальные элементы своих стратегий не меняют.

Преимущества равновесия Неша:

1. в большинстве моделей это равновесие существует, его можно определить.

Недостатки равновесия Неша:

1. данное равновесие не всегда единственное, в этом случае вводятся дополнительные предложения, чтобы устранить неопределенность

2. равновесие по Нешу не устойчиво к отклонению двух и более игроков.

Лекция №10. 18.04.05

Тема: Постановка задач согласования экономических интересов.

В организационной системе имеет место два вида взаимодействия:

1. горизонтальное (сослуживцы)

2. вертикальное (начальник-подчиненные).

Вертикальное взаимодействие. Центральный орган осуществляет решение задач управления деятельностью элементами – планирование.

Общая постановка:

П – плановое задание, которое обеспечивает экстремум его целевой функции

Х – элементы отрабатывают эти планы и достигают некоторых экономических результатов.

П – желаемое состояние системы с точки зрения оценки

Х – фактическое состояние системы.

1…n – исполнительные элементы.

Управленческой стратегией элемента является х.

В формализованном виде модель принятия решений исполнителем приобретает следующий вид:

Если целевые функции центра Ф и целевые функции элементов не совпадают или не согласованы, то в силу активности исполнительных элементов фактические результаты могут не соответствовать оптимуму всей системы в целом.

Существовали жесткие централизованные системы: пример во время ВОВ на заводах абсолютно не было опозданий на работу.

В настоящее время не так. Сейчас применяют методы согласования интересов.

Одним из подходов согласования являются методы согласования планирования.(необходимо учитывать интересы элементов).

В формализованном виде этот подход имеет следующую запись:

Назначаемые планы должны давать возможность получить максимальную выгоду исполнителю.

Недостаток подхода: попытка «идти на поводу» у элементов может приводить к снижению эффективности всей системы в целом.

Второй подход согласование интересов – параметрическое согласование.

Пусть в системе имеются некоторые параметры, которые являются общими для всех элементов. Допускаем также, что центр имеет юридическую и экономическую возможность варьирования этим параметром.

Тогда назначая то или иное значение параметра центр как игрок, задающий правила игры, может обеспечить согласование экономических интересов участников взаимодействия.

Пример.

Минимум общих затрат

R – общая производственная программа

Оптимальное значение рассчитывается таким образом:

(1)

Получили закон пропорционального распределения.

r_i – показатель эффективности работы предприятия.

Пусть r₁ = 1, r₂ = 2, r₃ = 3, R = 180, Ц = 40

Х₁⁰ = 1*180/6 = 30

Х₂⁰ = 60

Х₃⁰ = 90

У элементов есть свои интересы.

Х_i¹ = Ц*r_i – интерес производственного элемента.

Х₁¹ = 40*1 = 40

Х₂¹ = 80

Х₃¹ = 120

Затраты

Выручка

Прибыль

х

30 40

Угол наклона зависит от цены. Локальный интерес для первого элемента 40, мы даем ему 30, тем самым лишаем его кусочка прибыли.

Пусть применяется метод формирования данных. Каждый элемент сообщает S_i – оценка показателя эффективности. Предположим существует диапазон дополнительных изменений:

d_i ≤ S_i ≤ D_i

Выбор S_i – управленческая стратегия i –го элемента на этапе планирования.

(2) – модель планирования в случае применения процедуры формирования данных.

Плановое задание x_i зависит от той оценки, которую элемент сообщает.

Чтобы получить больше прибыли, элемент будет завышать свою оценку.

Пусть d_i = 1, D_i = 5, S_i^p – равновесие

S₁^p = 5, x₁ =5*180/15 = 60 (хотел 40, дали лишнюю программу)

S₂^p = 5, x₂ = 60 (хотел 80, не додали программу)

S₃^p = 5, x₃ = 60 (ему хотелось получать 120)

Рассчитаем оценку для первого элемента:

Х₁ = S₁*180/5+5+S₁ = S₁*180/10+S₁

40 = 180*S₁/10+S₁

S₁ = 2.857

X₁ = 2.8*180/5+5+2.8 = 39.4 ≈ 40

x₂ = x₃ =70 (180-40=140, 140/2=70)

Цена – общий параметр.

В некоторых случаях можно внедрять так называемые внутрипроизводственные механизмы, и в них назначать внутрифирменные цены.

Каждый i- элемент при некоторой цене заинтересован выпускать x_i = Ц*r_i, V = Σr*x_i = ΣЦ*r_i.

V – желаемый объем производства, который хотели бы выпустить исполнители будь на то их воля.

V ≠ R

Обнаружив это, у центра возникнет идея перейти на внутренние цены: х_i¹ = Ц^в * r_i. В этом случае будут согласованы интересы.

3. V=R, S_i^p =r_i

4. V>R, S_i^p = D_i

5. V<R, S_i^p = d_i.

V = ∑Ц^в * r_i = R

(3)

В процедуре формирования данных дополняется механизм ценообразования.

(4) – модель механизма ценообразования.

- модель механизма согласованного параметрического управления.

Предположим V>R. В этом случае у каждого элемента имеется желание получить большее задание.

Чтобы достичь этого элементы будут завышать заявки.

↑ Х_i →↑S_i →↓Ц^в →↓х_i

↓

↓ S_i

Получилась отрицательная обратная связь.

Все это образует механизм согласования цены.

При достаточно большом n данного механизма обеспечивается равновесие сообщения достоверности заявок.