
СБОРНИК РАСЧЕТНО-ПРОЕКТИРОВОЧНЫХ РАБОТ ПО СОПРОТИВЛЕНИЮ МАТЕРИАЛОВ
.pdfформуле |
|
|
i |
|
Ni i |
T |
i |
|
. Так как напряжения уже вычислены, |
||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
EA |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|||
то воспользуемся формулой |
i |
|
|
|
i |
|
i |
|
a T |
i |
= |
|
|
a T |
i |
||||||||||||||||||||||
|
|
E |
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E |
|
|||||||||
|
|
|
|
247,6 106 |
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
||||||||
|
I |
|
|
|
|
|
|
|
|
|
12,5 10 |
|
|
20 |
|
0,75 1,116 10 |
|
|
м 1,116мм, |
||||||||||||||||||
|
|
|
11 |
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
2 10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
106,1 106 |
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|||||||||||
II |
|
|
|
|
|
|
|
|
|
12,5 10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
м 0,585мм, |
||||||||||
|
|
|
|
11 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
20 0,75 5,854 10 |
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
2 10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
119,4 106 |
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
||||||||
|
III |
|
|
|
|
|
|
|
|
12,5 10 |
|
|
20 |
|
1 8,47 10 |
|
м 0,847мм, |
|
|
||||||||||||||||||
|
|
|
11 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
2 10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
IY |
0 12,5 10 6 20 0,5 1,25 10 4 |
м 0,125мм, |
|
|
|
|
|||||||||||||||||||||||||||||||
Перемещения сечения бруса вычислим по формуле:
ui ui 1 i , где i 0,I,II,III,IY - номера границ между
участками, нулевая граница относится к заделке верхней опоры, граница IY совпадает с нижним концом бруса.
u0 0, uI u0 I 1,116мм,,
uII uI II 1,116 0,585 1,701мм, uIII uII III 1,701 0,847 2,548мм, uIY uIII IY 2,548 0,125 2,673мм.
По вычисленным значениям нормальных сил, нормальных напряжений и перемещений построим соответствующие эпюры (рис.2).
Марку стали назначим из условия прочности при центральном
растяжении - сжатии: |
|
|
|
|
|
Т |
, |
||||||
|
|
||||||||||||
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
наиб |
|
n |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
T |
|
T |
nT |
|
|
|
наиб |
1,5 247,6 371,4МПа . |
|||||||
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
||||
Этому пределу текучести будет соответствовать сталь 45Г2, у которой Т 400МПа .
11
Брус с нижней опорной поверхностью
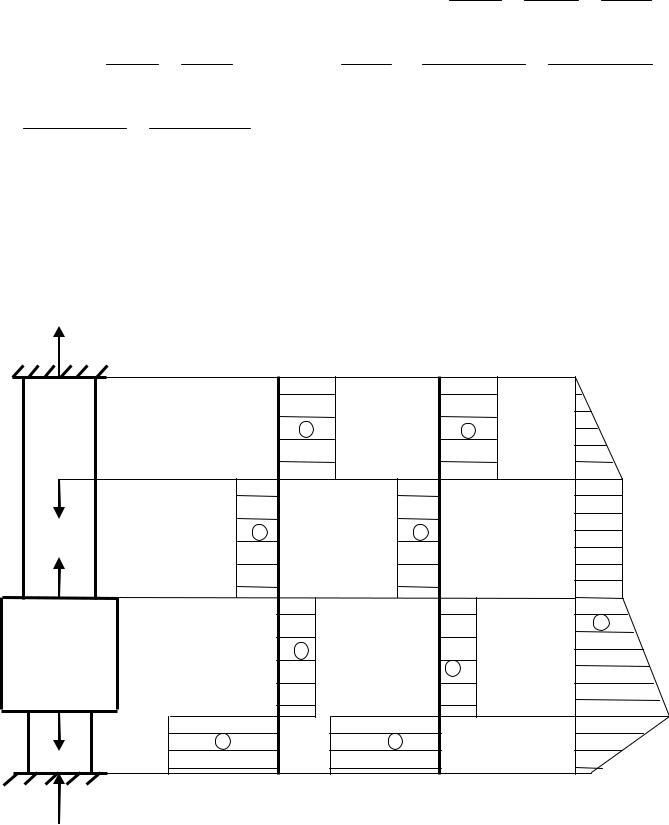
После приложения нагрузки и изменения температуры брус удлинится и коснется нижней опорной поверхности. В обеих опорных
поверхностях появятся реакции RA и RB (рис. 4). |
|
|
Составим уравнение статики:RA F1 F2 F4 RB |
0, |
(1) |
из которого следует, что задача статически неопределима, так как для
определения двух неизвестных сил имеем лишь одно уравнение. |
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
Составим уравнение совместности деформаций бруса: |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
IY |
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2) |
|
|
|
|
||||
|
l |
|
|
lT |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
i 1 |
|
iN |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
где l |
iN |
= |
Ni i |
|
удлинения участков бруса от действия нормальных |
|||||||||||||||||||||||||||||||||||||
|
EA |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
сил; |
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
lT |
|
|
T температурное удлинение бруса. |
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
2 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Определим методом сечений нормальные силы на каждом участке |
|||||||||||||||||||||||||||||||||||||||||
бруса: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
NI RA,NII |
RA F1,NIII |
RA F1 |
F2 ,NIY RA F1 F2 F4 . |
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
Подставим эти |
|
значения нормальных сил в уравнение (2): |
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
||||
|
RA I |
|
|
|
(RA F1 ) II |
|
|
(RA F1 F2 ) III |
|
|
(RA |
F1 F2 |
F4 ) IY |
|
|
|
|
|||||||||||||||||||||||||
|
EAI |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
EAIY |
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
EAII |
|
|
|
|
|
|
|
|
EAIII |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
T ( 1 2 3 ). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
Из этого уравнения следует |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
E T( |
|
|
|
|
|
) F ( |
II |
|
|
III |
|
|
IY |
) F ( |
III |
|
IY |
) F |
IY |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
A |
||||||||||||||||||||||||||||||
RA |
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
|
3 |
|
|
1 A A |
|
|
|
A |
2 A |
|
A |
4 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
II |
|
|
III |
|
|
|
|
IY |
|
III |
|
IY |
|
IY |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I |
|
II |
|
III |
|
|
IY |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
AI |
AII |
AIII |
|
AIY |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
12
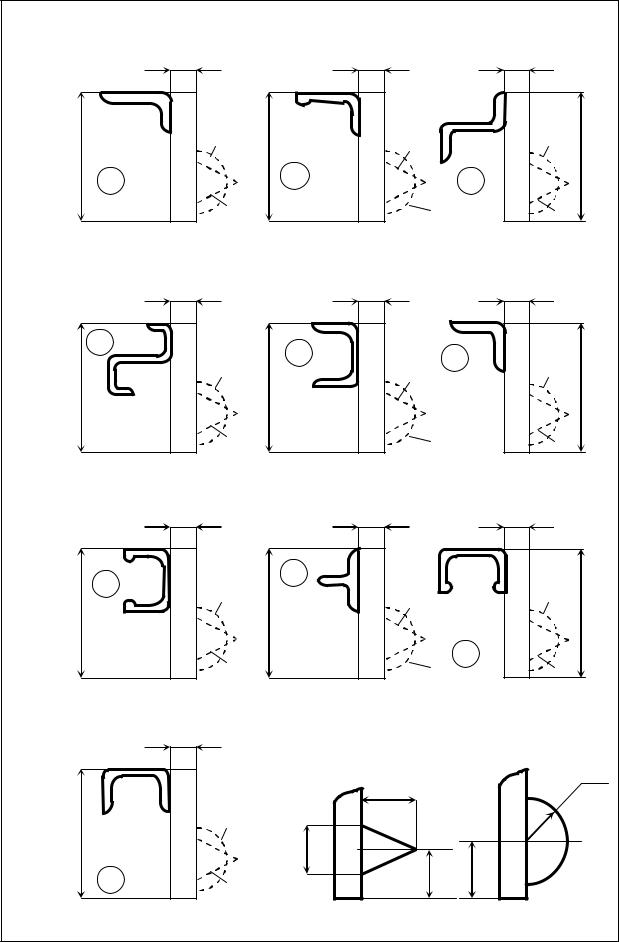
(2 1011(0,1 10 3 12,5 10 6 20 3) 400 107 ( |
0,75 |
|
1 |
|
0,5 |
) |
||||||
|
|
|
|
|
|
|
28,27 |
|
50,27 |
|
12,57 |
|
300 107 ( |
1 |
|
0,5 |
) 600 107 0,5 |
):( |
0,75 |
|
|
0,75 |
|
||
|
|
50,27 |
12,57 |
12,57 |
28,27 10 4 |
28,27 10 4 |
|
|||||
|
1 |
|
|
0,5 |
) 243,5кН. |
|
|
|
|
|
|
|
|
50,27 10 4 |
12,57 10 4 |
|
|
|
|
|
|
|
|||
|
|
|
|
NI 243,5кН , |
|
|
|
|
|
|
|
|
|
|
|
|
NII =243,5 – 400 = -156,5кН, |
|
|
|
|
|
|||
|
|
|
|
NIII =243,5 – 400 + 300 = 143,5кН, |
|
|
|
|
||||
|
|
|
|
NIY =243,5 – 400 + 300 – 600 = - 456,5кН. |
|
|
||||||
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
RA 243,5кН |
N, кН |
σ, МПа |
|
u, мм |
|
|
|||||
|
I |
|
|
243,5 |
|
|
86,1 |
|
|
|
||
|
|
|
+ |
|
+ |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||
|
F1 400кН |
156,5 |
55,4 |
|
|
|
|
0,5 |
|
|||
|
II |
|
|
- |
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
F2 300кН |
|
143,5 |
|
28,6 |
|
|
|
0,4 |
|||
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
III |
|
|
+ |
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F4 600кН |
456,5 |
363,2 |
|
|
|
|
|
|
|
||
|
- |
|
- |
|
|
|
|
|
|
|||
|
|
IY |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
0,103 |
|
|
|
RB |
456,5кН |
Рис.4 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
13 |
|
Вычислим нормальные напряжения на каждом участке:
|
|
|
|
|
|
|
|
|
N |
I |
|
|
|
|
|
|
243,5 103 |
|
86,1МПа , |
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
I |
|
|
A |
|
|
|
|
|
|
28,27 10 4 |
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
N |
|
II |
|
|
|
|
|
156,5 103 |
|
|
55,4МПа , |
|
|
|
|
|
|||||||||||||||||||||||||
|
|
II |
|
|
|
A |
|
|
|
|
|
28,27 10 4 |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
II |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
N |
III |
|
|
|
|
|
143,5 103 |
|
|
28,6МПа, |
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
III |
|
|
|
A |
|
|
|
|
50,27 10 4 |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
III |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N |
IY |
|
|
|
|
|
456,5 103 |
363,2МПа. |
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
IY |
|
|
|
|
A |
|
|
|
|
12,57 10 4 |
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
IY |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Определим абсолютные удлинения участков бруса: |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
N |
I |
|
|
I |
|
|
|
T |
|
|
|
|
243,5 103 0,75 |
|
|
|
|
|||||||||||||||||||||||||||
I |
|
|
|
|
|
|
EA |
|
|
|
|
|
|
|
I |
2 1011 28,27 10 4 |
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12,5 10 6 |
|
0,75 20 6,625 104 |
м 5,0984 10 4 м 0,51мм; |
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
N |
II |
|
|
II |
|
|
|
|
T |
|
|
|
156,5 103 0,75 |
|
|
|||||||||||||||||||||||||||
II |
|
|
|
|
|
|
|
|
|
|
II |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
EA |
|
|
|
|
|
|
|
|
2 1011 28,27 10 4 |
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
II |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
12,5 10 6 0,75 20 0,201 10 4 м 0,02мм. |
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
NIII |
|
|
III |
|
|
T |
|
143,5 103 |
1 |
|
||||||||||||||||||||||||||||||||
III |
|
|
|
|
|
|
EA |
|
|
|
|
|
|
III |
2 1011 50,27 10 4 |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
III1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
12,5 10 6 1 20 3,927 10 4 м 0,393мм; |
|
||||||||||||||||||||||||||||||||||||||||||||||
IY |
|
N |
IY |
|
|
l |
IY |
|
IY |
T |
|
|
456,5 1030,51 |
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
EA |
|
|
|
|
|
|
|
|
|
|
2 1011 12,57 10 |
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
IY |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12,5 10 6 0,5 20 7,829 10 4 м 0,783мм. |
|
||||||||||||||||||||||||||||||||||||||||||||||||
Определим перемещение границ между участками: |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u0 0 ; |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
uI |
|
u0 |
|
I |
|
0 0,51 0,51мм; |
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
uII |
|
uI |
|
|
|
II |
|
|
0,51 0,02 0,49мм;. |
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
uIII |
|
|
uII |
III |
0,49 0,393 0,883мм; |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
uIY |
|
|
uIII |
III 0,883 0,78 0,103мм. |
|
|||||||||||||||||||||||||||||||||||||
Перемещение нижнего конца бруса должно равняться зазору .
14

Вычислим погрешность решения:
|
uIY |
|
|
100% |
|
0,103 0,1 |
|
100% 3%. |
|
|
|
|
|
|
|
||
|
|
|
|
|
0,1 |
|
||
|
|
|
|
|||||
Погрешность в пределах допускаемой.
По вычисленным значениям нормальных сил, нормальных напряжений и перемещений построим соответствующие эпюры (рис.4).
Подберём материал для рассмотренного статически
неопределимого бруса: Т nT 363,2 1,5 544,8МПа. Этому
наиб
условию прочности может соответствовать сталь 20Х, у которой Т 550МПа.
ЛИТЕРАТУРА
1. Феодосьев В.И. Сопротивление материалов [Текст]: Учебник для втузов / В.И. Феодосьев. - М.: МГТУ им. Баумана, 2007. - 512 с.
2.Справочные данные к расчетно-проектировочным и курсовым работам по сопротивлению материалов[Текст]: Методические указания, Ч.1 / В.К. Шадрин, В.С. Вакулюк, В.Б. Иванов, В.А. Кирпичев, С.М. Лежин. - Самара: СГАУ, 2007. – 36 с.
15
Работa № 2
ОПРЕДЕЛЕНИЕ ГЕОМЕТРИЧЕСКИХ ХАРАКТЕРИСТИК ПОПЕРЕЧНОГО СЕЧЕНИЯ БРУСА
1. ПОСТАНОВКА ЗАДАЧИ
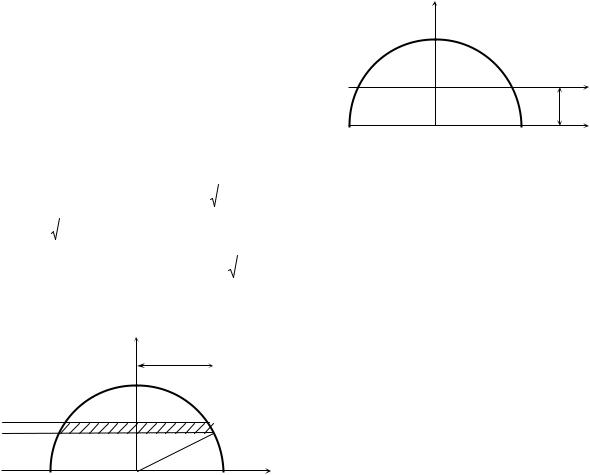
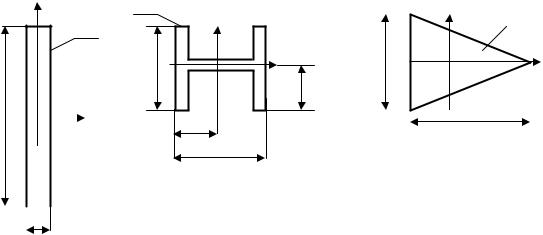
Заданы поперечное сечение бруса сложной формы, составленное из отдельных элементов, и размеры элементов (рис. 1).
Требуется определить положение главных центральных осей, главные центральные моменты инерции сечения, моменты сопротивления изгибу, построить эллипс инерции. Поставленную задачу решить аналитическим и графическим способами.
В пояснительной записке следует представить реферат, чертеж сечения, выполненный в масштабе с изображением центральных и главных центральных осей, эллипса инерции, круг Мора и все необходимые расчеты.
2.ВЫБОР ЗАДАНИЯ
Студенту выдается трехзначный номер, например 376, который следует записать два раза 376 376. Под цифрами следует записать шифр, состоящий из шести букв а, б, в, г, д, е:
376 376
абв где
Цифра над буквой указывает, какую строку следует взять в соответствующем столбце таблицы. Номеру 376 соответствуют следующие данные: схема № 3, вариант А (в нижней части сечения равнобедренный треугольник), = 4 мм, l = 60 мм, h = 50 мм,
r = 20 мм, b = 15 мм, с = 0,5 l = 30 мм, Пр 105 № 1.
3.ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1.Поданным таблицы, соответствующим заданному шифру, вычерчивают в масштабе сечение.
Размеры и геометрические характеристики авиационных
алюминиевых профилей Пр приведены в пособии [2 .
16
|
|
|
|
|
|
|
|
|
|
|
|
Пр-105 |
|
Пр-101 |
Б |
l |
Пр-102 |
А |
|
Бl |
l |
|
|
2 |
|
|
|
1 |
|
|
|
3 |
|
|
|
А |
|
|
Б |
А |
|
|
|
|
|
|
|
|
4 |
|
|
5 |
|
6 |
|
|
Б |
|
А |
Б |
||
l |
l |
|
Пр-100 |
|||
|
|
|
l |
|||
|
|
|
|
|
|
|
Пр-104 |
А |
Пр-106 |
|
Б |
А |
|
|
|
|
||||
|
|
|
|
|
|
|
7 |
Б |
|
8 |
|
|
Бl |
|
|
А |
|
|||
l |
l |
|
|
|||
|
|
|
Пр-107 |
|
||
Пр-107 |
|
|
Пр-109 |
|
|
|
|
А |
|
|
9 |
А |
|
|
|
|
Б |
|||
|
|
|
Вариант А |
Вариант Б |
||
|
|
|
||||
|
|
|
|
h |
|
r |
|
|
|
|
|
|
|
l |
Б |
|
|
|
|
|
Пр-106 |
|
|
b |
|
|
|
|
|
|
c |
c |
|
|
10 |
|
А |
|
|
||
|
|
|
|
|
||
|
|
|
Рис. 1 |
|
|
|
17

№ строки |
№ схемы |
|
вариант |
|
|||
|
|
|
|
Т а б л и ц а
В ы б и р а е м ы е п а р а м е т р ы
, |
l, |
h, |
R, |
b, |
с |
|
|
Н о м е р а п р о ф и л е й |
|
|
||||
|
|
|
|
|
|
|
|
|
||||||
мм |
мм |
мм |
мм |
мм |
|
Пр100 |
Пр101 |
Пр102 |
Пр104 |
Пр105 |
Пр106 |
|
Пр107 |
Пр109 |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
А |
3 |
60 |
30 |
25 |
15 |
0,5l |
9 |
4 |
7 |
1 |
1 |
4 |
1 |
1 |
2 |
2 |
Б |
4 |
70 |
40 |
15 |
20 |
0,4l |
10 |
5 |
8 |
2 |
2 |
5 |
3 |
2 |
3 |
3 |
А |
5 |
80 |
50 |
20 |
30 |
0,3l |
11 |
6 |
9 |
3 |
3 |
6 |
4 |
3 |
4 |
4 |
Б |
6 |
90 |
30 |
25 |
15 |
0,2l |
12 |
7 |
10 |
4 |
4 |
7 |
5 |
4 |
5 |
5 |
А |
3 |
100 |
40 |
15 |
20 |
0,5l |
13 |
8 |
11 |
5 |
5 |
8 |
6 |
1 |
6 |
6 |
Б |
4 |
60 |
50 |
20 |
30 |
0,4l |
9 |
4 |
7 |
1 |
1 |
4 |
1 |
2 |
7 |
7 |
А |
5 |
70 |
30 |
25 |
15 |
0,5l |
10 |
5 |
8 |
2 |
2 |
5 |
3 |
3 |
8 |
8 |
Б |
6 |
80 |
40 |
15 |
20 |
0,2l |
11 |
6 |
9 |
3 |
3 |
6 |
4 |
4 |
9 |
9 |
А |
4 |
90 |
50 |
20 |
30 |
0,5l |
12 |
7 |
10 |
4 |
4 |
7 |
5 |
1 |
0 |
10 |
Б |
5 |
100 |
30 |
25 |
15 |
0,4l |
13 |
8 |
11 |
5 |
5 |
8 |
6 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а |
б |
в |
|
|
г |
|
д |
|
|
|
|
е |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
18
2.Выбирается произвольная система координатных осей, относительно которых определяется положение центра тяжести сечения, и проводятся центральные оси сечения, наиболее рациональные для решения задачи.
3.Вычисляются осевые и центробежные моменты инерции каждой части сечения и моменты инерции всего сечения относительно центральных осей.
4.Вычисляются главные центральные моменты инерции сечения и определяется положение главных центральных осей. Эта задача решается аналитически и графически с помощью круга Мора. Подсчитываются моменты сопротивления сечения изгибу.
5.Вычисляются главные радиусы инерции и строится эллипс инерции.
4.КОНТРОЛЬНЫЕ ВОПРОСЫ
1.Как определяют положение центра тяжести сечения?
2.Какие оси называются главными?
3.Сколько главных осей имеет сечение?
4.Для каких сечений можно, не прибегая к расчетам, установить положение главных осей?
5.Как изменится центробежный момент инерции сечения при повороте осей на 90°?
6.Каким свойством обладает сумма осевых моментов инерции относительно двух взаимно перпендикулярных осей?
7.Для какой цели строят эллипс инерции?
5.ПРИМЕРЫ
Пример 1. Определить положение центра тяжести |
|
|
|
y0 |
|||||||||||||||||
и главные центральные моменты инерции сечения, |
|
|
|
|
|
|
|||||||||||||||
изображенного на рис. 2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Положение центра тяжести сечения определим по |
|
|
|
|
|
|
|||||||||||||||
формуле |
|
|
|
|
|
|
|
A ydA |
|
|
|
|
|
|
|
|
c |
|
x0 |
||
|
|
|
|
|
|
SX |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
c |
||||
|
|
|
c |
|
|
, |
|
|
|
|
|
|
|
|
|
|
y |
||||
|
A |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
x |
||||
где Sx статический момент сечения относительно оси |
|
|
|
0 |
|
||||||||||||||||
|
|
|
|
|
|||||||||||||||||
х; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 2 |
||
A площадь сечения. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
r2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
A |
, |
|
|
dA 2xdy 2 r2 |
y2 dy, |
|
|
|
|
|
|
||||||||||
2 |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где x |
r2 y2 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
r |
|
|
|
dy 2 r2 |
y2 3/ 2 |
|
r 2r3 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
ydA 2y |
|
r2 y2 |
|
, |
|
|||||||||
|
|
|
|
|
|
|
A |
0 |
|
|
3 |
|
|
|
0 |
3 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
y dy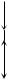
|
|
|
|
|
y |
|
2r3 2 |
|
4r |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
y |
|
|
|
|
c |
|
3 r2 |
3 |
|
|
|
|
|
|||||||
|
|
В связи с симметрией сечения xC 0 . |
|
|
||||||||||||||||
|
|
|
||||||||||||||||||
x |
|
|
Отметим положение |
|
|
центра |
тяжести |
и, |
|
|||||||||||
|
|
|
|
учитывая симметрию сечения, проведем главные |
||||||||||||||||
|
|
|
|
центральные оси xo, yo (рис. 2). |
|
|
|
|
|
|||||||||||
|
|
|
|
Определим |
главные |
центральные моменты |
|
|||||||||||||
|
|
|
|
инерции: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
r4 |
|
|
|
4r |
2 |
r2 |
|
|
||||||||||
2 |
|
|
|
|
4 |
|||||||||||||||
|
|
|
x |
Ix0 Ix yc |
A |
|
|
|
|
|
|
|
|
|
|
|
0,11r |
|
||
|
8 |
|
|
|
2 |
|
||||||||||||||
0 |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
3 |
|
|
|
|
||||||||
Рис. 3 |
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
I |
|
|
|
r4 |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
y0 |
8 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Пример 2. Заданы поперечное сечение бруса сложной формы составленное, составленное из
19
профиля ПР125-2, пластин прямоугольной и треугольной формы, и размеры этих элементов.
Требуется вычислить главные центральные моменты инерции сечения, определить положение главных центральных осей аналитическим и графическим способами, вычислить моменты сопротивления изгибу и радиусы инерции, построить эллипс инерции.
Исходные данные: δ=6мм, ℓ=100мм, h = 42мм, b = 30мм, с = 0,3ℓ = 30мм, Пр-125-2.
Решение
1. Из справочных данных 2 выписываем геометрические характеристики профиля и вычерчиваем в масштабе заданное поперечное сечение (рис.5). Пронумеруем элементы этого сечения, проведём собственные центральные оси для каждого из них, относительно которых
у1 |
|
2 |
|
|
1 |
|
|
у2 |
|
|
|
|
||
|
|
см |
|
х2 |
ℓ=10см |
|
|
|
|
х1 |
В=3 |
1,25см |
1,5см |
|
|
|
|
|
Н=2,5см
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
2,14см2, |
|
|
|
|
δ=0,6см |
2 |
|||||||||||
|
|
|
I |
|
1,099см4, |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
А1=ℓ∙δ=10∙0,6=6см2, |
Iy2 |
4,499см4 |
|||||||||||||
|
Ix |
|
3 |
|
|
0,6 103 |
|
50см4, |
|
|
|
||||
|
|
|
|
|
|
|
|
||||||||
1 |
12 |
|
12 |
|
|
|
|
|
|||||||
|
Iy |
|
3 |
|
0,63 10 |
0,18см4 |
|
|
|||||||
|
|
|
|
|
|||||||||||
1 |
12 |
|
12 |
|
|
|
|
Рис.4 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
у3 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
b=3см |
x3 |
|||
|
|
|||
|
|
|||
|
h=4,2см |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
A |
bh |
|
3 4,2 |
6,3см2, |
|
|
|||||||||||
2 |
|
|
|
|
|||||||||||||
, |
3 |
|
|
|
|
2 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
3 |
|
|
|
|
|
|
|||
|
|
|
|
|
2h |
|
|
|
|
2 4,2 1,53 |
|
|
|||||
|
|
|
|
2 |
|
|
|
||||||||||
I |
x3 |
|
|
|
|
|
|
|
2,36см |
4 |
|||||||
12 |
|
|
|
|
|
12 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Iy |
|
|
bh3 |
|
3 4,23 |
6,174см4 |
|
||||||||||
|
|
|
|
||||||||||||||
|
|
3 |
|
36 |
|
|
|
|
36 |
|
|
|
|||||
вычислим моменты инерции (рис.4) .
2. Определим координаты центра тяжести в произвольных осях U,V, параллельных
центральным осям элементов, используя формулы:
|
3 |
|
|
3 |
|
|
V |
Ai Vci |
, U |
|
|
Ai Uci |
|
i 1 |
c |
i 1 |
, |
|||
3 |
|
|||||
c |
|
3 |
|
|||
|
Ai |
|
|
|
Ai |
|
|
i 1 |
|
|
|
i 1 |
|
где Vci , Uci - координаты центров тяжестей элементов сечения в координатных осях U,V.
V |
|
|
|
10 |
5см, U |
H |
|
2,5 0,3 2,8см, |
|
|
2 |
||||||
c1 |
2 |
2 |
|
c1 |
|
|||
20
