4.5.3. Моделирование финансовых потоков в среде Excel

Задача моделирования финансовых потоков возникает при решении задач финансового менеджмента, т.е. управлении вложением свободных средств в различные инвестиционные проекты. Основная цель финансового менеджмента – сохранение и приумножение денежных средств инвестора.

4.5.3.1. Инвестиционный цикл

Интервал времени, в течение которого инвестиционный проект осуществляется от разработки идеи до ликвидации проекта, называется инвестиционным циклом или жизненным циклом инвестиционного проекта (рис. 4.12).

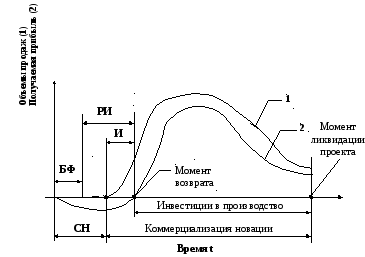
Рис. 4.12. Жизненный цикл инвестиционного проекта

(Пояснить рисунок)

В пределах жизненного цикла можно выделить несколько принципиально важных интервалов времени: бюджетное финансирование (БФ), рискоинвестиции (РИ), инвестирование проекта (И), инвестирование средств в производство. Риск потери вложенных денег убывает по мере перехода от одного интервала к другому.

4.5.3.2. Инструментарий Excelдля моделирования финансовых потоков

Основными проблемами финансового менеджмента являются проблема отбора проектов для инвестирования и распределение средств между ними. Вторая задача была рассмотрена ранее. Не менее важна подготовительная работа (выбор проектов для инвестирования), связанная со сложными финансовыми расчетами, определяющими прибыли и убытки, возможные при реализации проектов. Выбор проектов для инвестирования осложняется следующими обстоятельствами:

• изменение "цены" денег во времени;

• многообразие способов начислений процентов на вложенный капитал инвестора;

• многообразие способов расчетов по ценным бумагам;

• необходимость учета изменения стоимости основных средств во времени.

(Прокомментировать)

Следует обеспечить сопоставимость денежных сумм. Поэтому их приводят к началу осуществления проекта или к концу осуществления проекта. Процесс приведения денежных сумм к началу и к концу проекта (рис. 4.13). Обозначив норму прибыли в j-й период черезp_j, выразим дисконтированную и накопленную суммы следующими выражениями:

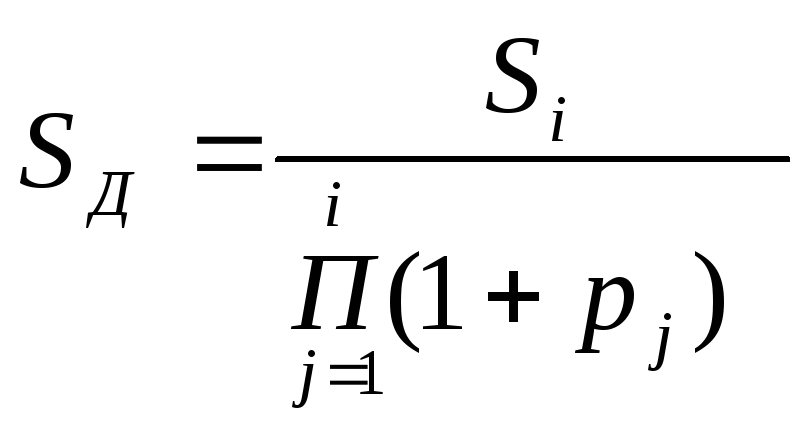(4-5)

(4-6)

Если норма прибыли постоянна для всех периодов и равна p, то выражения (4-5) и (4-6) примут вид:

(4-5')

(4-6')

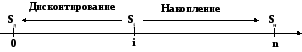
t, пер

Рис. 4.13. Дисконтированная и накопленная суммы

Величины S_диS_нмогут служить мерой эффективности инвестиционного проекта. Особенно часто в качестве характеристики эффективности инвестиционного проекта применяется величинаS_д.

Кроме указанных величин эффективность инвестиционного проекта может быть охарактеризована следующими параметрами:

• чистый дисконтированный доход (ЧДД);

• индекс доходности (ИД);

• внутренняя норма доходности (ВНД);

• срок окупаемости.

Перечисленные показатели определяются по формулам:

(4-7)

(4-7')

(4-8)

ВНД - корень p уравнения

(4-9),

где		- сумма дисконтированных капитальных вложений
	Ri, Ki,Зi, З'I	- результаты, достигнутые на i-том шаге расчета, капиталовложения на этом шаге, затраты с учетом и без учета капиталовложений на указанном шаге расчета соответственно.

Изменение с течением времени стоимости основных средств учитывается начислением амортизации.

Среди ценных бумаг различают долгосрочные и краткосрочные, с регулярным и нерегулярным сроком выплаты процентов, с выплатой всей суммы при погашении и т.д.

Табличный процессор Excelимеет достаточно богатый набор функций, позволяющих вычислять показатели эффективности инвестиционного проекта, параметры проекта, обеспечивающие необходимую эффективность, выполнять амортизационные начисления, а также выполнять различные расчеты по ценным бумагам [17].

Непосредственно для вычисления S_дпредназначены функции ПЗ, НПЗ и ЧИСТНПЗ, а для вычисленияS_н– БЗ, БЗРАСПИС. Указанные функции позволяют также учесть все многообразие способов платежей и начисления процентов.

Кроме финансовых функций табличный процессор Excelимеет такие инструменты моделирования финансовых потоков как таблицы подстановок и сценарии расчета.

Таблица подстановок позволяет выполнить многократный расчет функции одного или двух аргументов по формуле, помещенной в одну ячейку. Соответственно различают два типа таблиц подстановок – одномерные и двумерные. Схема подготовки данных и окно создания таблицы подстановок приведены на рис. 4.14.

A B C 1 Тестовые данные 2 X= <XT> Формула 3 <X1> 4 <X2> 5 <X3> 6 . . . а) A B C 1 Тестовые данные 2 X= <XT> 3 <XT> Формула 4 <X1> 5 <X2> 6 <X3> 7 . . .	A B C D E 1 Тестовые данные 2 X= <XT> 3 Z= <ZT> 4 Формула <Z1> <Z2> . . . 5 <X1> 6 <X2> 7 8 <X4> 9 . . . в)
б)	г)
Рис. 4.14. Схема построения одномерной (а,б) и двумерной (в) таблиц подстановок и окно создания таблицы подстановок (символы "<" и ">" указывают, что в клетке стоит число, а не комбинация обозначающих его символов)

(Прокомментировать рисунок)

Сценариями называются заранее подготовленные наборы данных, которые предполагается подставлять в некоторую формулу, размещенную на том же рабочем листе, где зарегистрированы сценарии. По сценариям может быть построен отчет, обобщающий данные сценариев и результаты расчетов. Примеры создания и применения сценария подсчета суммы данных двух клеток¹, а также получаемых в результате отчетов приведены на рис. 4.15.

Зарегистрировав на листе необходимое количество сценариев (в примере создано два сценария с числами 10,20 и 30,40) посредством диспетчера сценариев открывается окно "Отчет по сценарию" (рис. 4.15,г), в котором указывается тип отчета и адрес ячейки, содержащей результат. В результате в книгу Excelвставляются дополнительные листы с отчетами (рис. 4-15,д,е).

А В 1 =А1+А2+А3 2 а)		г)
б)	в)
д)		е)
Рис. 4.15. Схема подготовки данных для сценария (а) и окна, открываемые при построении и применении сценария (б–е)