
- •А.С. Березина, л.Н. Гавришина, а.Г. Седых математический анализ: дифференциальное исчисление
- •Оглавление
- •Ведение
- •1 Понятие функции
- •2 Предел функции
- •2.1 Понятие предела функции
- •2.2 Правила вычисления пределов
- •2.3 Непрерывность функции
- •3 Производная функции
- •3.1 Понятие производной и дифференциала
- •3.2 Правила дифференцирования
- •4 Использование производных для исследования функций
- •4.1 Возрастание, убывание функции. Точки экстремума
- •4.2 Выпуклость, вогнутость функции. Точки перегиба
- •4.3 Асимптоты графика функции
- •4.4 Общая схема исследования функции
- •5 Применение производной в экономических задачах
- •5.1 Предельные показатели в экономике
- •5.2 Понятие эластичности
- •5.3 Оптимальное значение экономических функций
- •6 Функция двух переменных
- •6.1 Частные производные. Градиент
- •6.2 Экстремум функции двух переменных
- •6.3 Условный экстремум функции двух переменных
- •7 Варианты контрольной работы
- •9 Контрольные вопросы для зачета
- •Что нужно уметь:
- •10 Контрольный тест для самопроверки
- •11 Задачи для самостоятельного решения
- •11.1 Понятие функции
- •11.2 Предел функции
- •11.3 Непрерывность функции Исследовать на непрерывность функцию , найти точки разрыва и указать характер разрыва.
- •11.4 Производная функции
- •11.5 Приложение производной
- •11.6 Применение производной в экономике
- •11.7 Функция многих переменных
- •Список литературы
- •Математический анализ: дифференциальное исчисление
- •650992, Г. Кемерово, пр. Кузнецкий, 39
11.5 Приложение производной
1. Найти пределы, используя правило Лопиталя
|
1.1. |
1.2.
|
1.3.
|
|
1.4.
|
1.5.
|
1.6.
|
|
1.7. |
1.8. |
1.9. |
|
1.10. |
1.11. |
1.12. |
|
1.13. |
1.14. |
1.15. |
|
1.16. |
1.17.
|
1.18.
|
2. Исследовать функцию и построить график.
|
2.1. y=x3 – 3x2 – 9x + 5 |
2.2. |
|
2.3.
|
2.4.
|
|
2.5.
|
2.6.
|
|
2.7.
|
2.8.
|
|
2.9.
|
2.10.
|
|
2.11.
|
2.12.
|
|
2.13.
|
2.14.
|
|
2.15.
|
2.16.
|
|
2.17.
|
2.18.
|
11.6 Применение производной в экономике
Зависимость издержек производства от объема выпускаемой продукции выражается формулой
 денежных единиц. Определить средние и
предельные издержки при объеме продукции
стоимостью
денежных единиц. Определить средние и
предельные издержки при объеме продукции
стоимостью ден.ед.
ден.ед.
Функция полных затрат в зависимости от объема выпускаемой продукции задана соотношением
 .
При каком объеме производства предельные
и средние затраты совпадают?
.
При каком объеме производства предельные
и средние затраты совпадают?
Себестоимость продукции y связана с объемом выпускаемой продукции х уравнением
 .
Определить среднюю и предельные
себестоимости выпускаемой продукции
при объеме, равном 10 ед.
.
Определить среднюю и предельные
себестоимости выпускаемой продукции
при объеме, равном 10 ед.
Зависимость спроса на товар определяется формулой
 .
Найти эластичность спроса при цене на
товар
.
Найти эластичность спроса при цене на
товар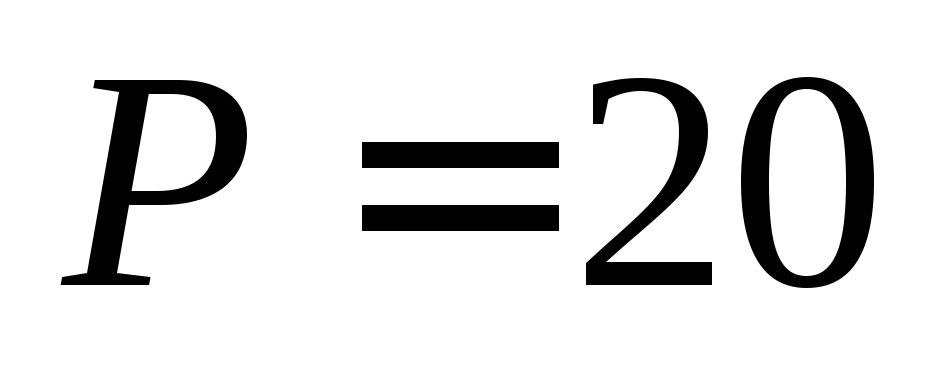 ден.ед.
ден.ед.
Зависимость между себестоимостью продукции
 и
объемом
и
объемом ее производства выражается формулой
ее производства выражается формулой .
Определить эластичность себестоимости
при выпуске продукции
.
Определить эластичность себестоимости
при выпуске продукции ден.ед.
ден.ед.
Функция долговременного спроса
 и предложения
и предложения от цены
от цены на мировом рынке нефти имеют,
соответственно, вид
на мировом рынке нефти имеют,
соответственно, вид ,
,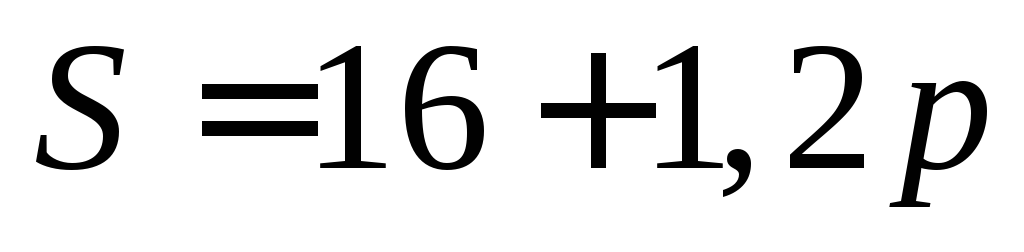 .
Найти эластичность спроса в точке
равновесной цены. Как изменится
равновесная цена и эластичность спроса
при уменьшении предложения нефти на
рынке на 25%?
.
Найти эластичность спроса в точке
равновесной цены. Как изменится
равновесная цена и эластичность спроса
при уменьшении предложения нефти на
рынке на 25%?
Функция спроса
 и предложения
и предложения от цены
от цены имеют, соответственно, вид
имеют, соответственно, вид ,
, .
Найти эластичность спроса и предложения
в точке равновесной цены. Как изменится
доход (в процентах) при увеличении цены
на 10%?
.
Найти эластичность спроса и предложения
в точке равновесной цены. Как изменится
доход (в процентах) при увеличении цены
на 10%?
Зависимость между издержками производства сигарет
 и процентным содержанием вредных
веществ в них
и процентным содержанием вредных
веществ в них выражается функцией
выражается функцией .
Найти средние и предельные издержки
производства, если количество вредных
веществ составляет 10%.
.
Найти средние и предельные издержки
производства, если количество вредных
веществ составляет 10%.
При подготовке к экзамену студент за
 дней изучает
дней изучает -ю
часть курса, а забывает
-ю
часть курса, а забывает -ю
часть. Сколько дней надо затратить
студенту на подготовку, чтобы была
изучена максимальная часть курса?
-ю
часть. Сколько дней надо затратить
студенту на подготовку, чтобы была
изучена максимальная часть курса?
Зависимость между спросом
 и
ценой
и
ценой единицы продукции задана соотношением
единицы продукции задана соотношением .
Найти значение цены, при которой спрос
будет нейтральным (с единичной
эластичностью).
.
Найти значение цены, при которой спрос
будет нейтральным (с единичной
эластичностью).
Доход от производства продукции с использованием
 единиц ресурсов составляет величину
единиц ресурсов составляет величину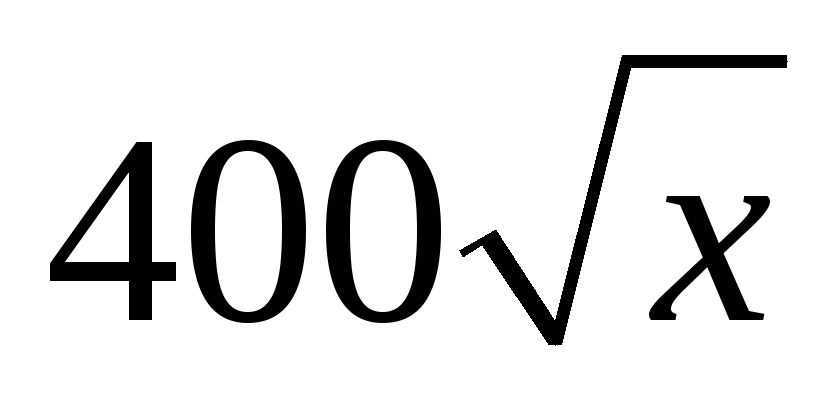 .
Стоимость единицы ресурсов – 10 денежных
единиц. Какое количество ресурсов
следует приобрести, чтобы прибыль была
наибольшей?
.
Стоимость единицы ресурсов – 10 денежных
единиц. Какое количество ресурсов
следует приобрести, чтобы прибыль была
наибольшей?
На начальном этапе производства фирма минимизирует средние издержки, причем функция издержек имеет вид
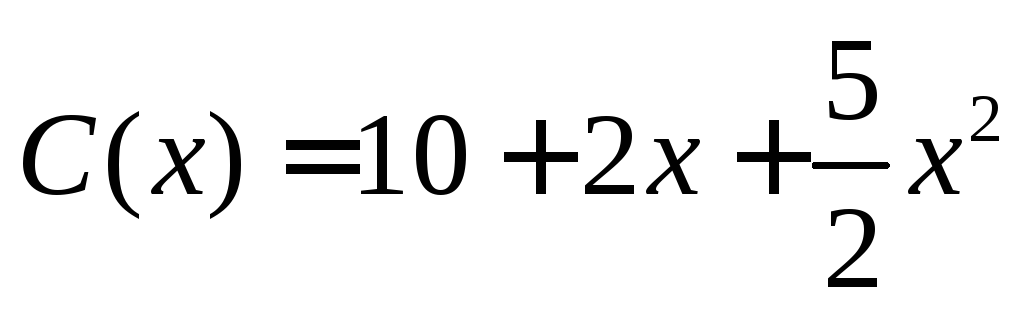 .
В дальнейшем цена единицы товара
устанавливается
.
В дальнейшем цена единицы товара
устанавливается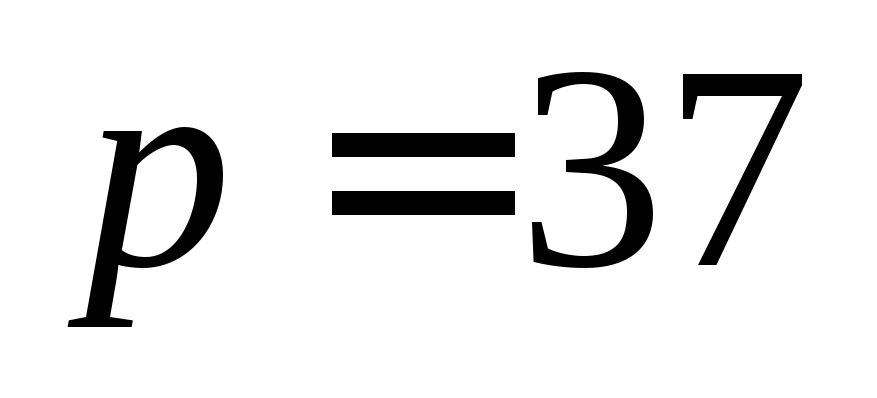 и фирма максимизирует свою прибыль. На
сколько единиц товара фирме следует
увеличить выпуск? На сколько при этом
изменятся средние издержки?
и фирма максимизирует свою прибыль. На
сколько единиц товара фирме следует
увеличить выпуск? На сколько при этом
изменятся средние издержки?
Функция издержек производителя имеет вид
 ,
гдеx
– объем производимой продукции. Весь
товар реализуется по фиксированной
цене 6 у.е. Определить функцию прибыли
производителя и объем выпуска, при
котором прибыль производителя будет
максимальной.
,
гдеx
– объем производимой продукции. Весь
товар реализуется по фиксированной
цене 6 у.е. Определить функцию прибыли
производителя и объем выпуска, при
котором прибыль производителя будет
максимальной.
Функция прибыли выписывается следующим образом:
 .
Определить оптимальный объем производства.
.
Определить оптимальный объем производства.
