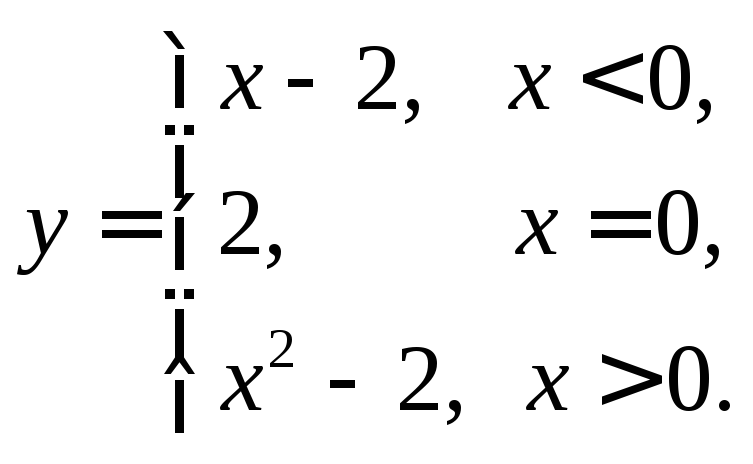11 Задачи для самостоятельного решения
11.1 Понятие функции
1. Найти области определения функций:
|
1.1. |
1.2. |
1.3. | ||
|
1.4. |
1.5. |
1.6.
| ||
|
1.7.
|
1.8. |
1.9. | ||
|
1.10. |
1.11. |
1.12. | ||
|
1.13. |
1.14.
|
1.15.
| ||
2.
По заданным функциям
построить сложную функцию
|
3.1.
|
3.2.
|
|
3.3.
|
3.4.
|
|
3.5.
|
3.6.
|
3.
Дано:
y=sinx;
v=lgy;
u=
.Выразить
u как функцию х.
4.
Дано:
y=1+x;
z=cosy;
.Выразить
v
как функцию х.
5.Следующие сложные функции представить с помощью цепочек, составленных из основных элементарных функций:
|
6.1. y=sin3(2x+1) |
6.2.
y= |
6.3. y=sin ln arcctg 2x |
|
6.4.
|
6.5. |
6.6. y=arccos ln tg 4x. |
6.
Построить области изменения переменной
х,
удовлетворяющей неравенствам: а)
;
б)
;
в)
.
7. Найти корни х1 и х2 функции у=4х-х2 и построить ее график на отрезке [x1-1; x2+1].
8. Исследовать функции на четность, нечетность.
8.1.
у=х4-2х2
8.2. y=cosx
8.3.
8.4.y=sinx-cosx
8.5.
y=tg
8.6.
8.7.
;
8.8.
;
9.
Дана функция
,
найти
.
10. Дано: f(x)=2x3-5x2-23x. Найти все корни уравнения f(x)=f(-2).
11. Найти функцию, обратную данной:
11.1.
y=x2-2x;
11.2.
;
11.3.
.
12.
Известно, что
,
а
.
Найти
.
13. Постоянные издержки, не зависящие от числа единиц произведенной продукции x, составляют 125 тыс. руб. в месяц, а переменные издержки (пропорциональные x) - 700 руб. за каждую единицу продукции. Цена единицы продукции равна 1200 руб. Составить функцию прибыли и найти объем продукции, при котором прибыль будет равна 105 тыс. руб. в месяц.
14.
Затраты на
производство продукции выражаются
функцией
,
гдеx
– число месяцев. Доход от реализации
продукции выражается функцией
.
Начиная с какого месяца производство
будет рентабельным?
15.
Доход от
реализации х
единиц продукции выражается функцией
.
Определить доход от реализации 10 единиц
продукции, если известно, что при
реализации 2 единиц доход составил 80
руб, а при реализации 4 единиц – 110 руб.
11.2 Предел функции
Найти пределы:
|
1.
|
2. |
3.
|
|
4.
|
5.
|
6.
|
|
7. |
8.
|
9.
|
|
10.
|
11.
|
12. |
|
13.
|
14. |
15.
|
|
16.
|
17.
|
18.
|
|
19.
|
20.
|
21.
|
|
22.
|
23.
|
24.
|
|
23.
|
24.
|
25.
|
|
26.
|
27.
|
28.
|
|
29.
|
30.
|
31.
|
|
32.
|
33.
|
34.
|
|
35.
|
36.
|
37.
|
|
38.
|
39.
|
40.
|
11.3 Непрерывность функции Исследовать на непрерывность функцию , найти точки разрыва и указать характер разрыва.
|
|
|
|
|
|
|
|
|
11.4 Производная функции
Найти производные функций.
|
1.
|
2.
|
3.
|
|
4.
|
5.
|
6.
|
|
7.
|
8.
|
9.
|
|
10.
|
11.
|
12. |
|
13.
|
14.
|
15.
|
|
16.
|
17.
|
18. |
|
19. |
20.
|
21.
|
|
22. |
23.
|
24.
|
|
25.
|
26.
|
27. |
|
28. |
29. |
30. |
|
31.
|
32.
|
33.
|
|
34.
|
35. |
36. |
|
37.
|
38.
|
39. |
|
40.
|
41. |
42.
|
|
43.
|
44. |
45.
|
|
46. |
47.
|
48. |
|
49.
|
50. |
51. |
|
52.
|
53. |
54.
|
.
Найти производные функций, заданных неявно.
|
|
|
|
|
|
5.
|
6.
|
|
7. |
8. |
9. |
Найти производные параметрических функций
|
1.
|
2.
|
3.
|
|
4.
|
5.
|
6.
|
