8.Вращающееся магнитное поле

Одним из важнейших достоинств трехфазной системы является возмож­ность получе­ния с ее помощью кругового вращающегося магнитного поля, ко­торое лежит в основе ра­боты трехфазных машин (генераторов и двигателей).

Для получения кругового вращающегося магнитного поля необходимо и достаточно выполнить два условия. Условие первое: необходимо 3p одинако­вых катушки (p =1, 2, 3,….) расположить в пространстве так, чтобы их оси были расположены в одной плоскости и сдви­нуты взаимно на равные углы ∆α=360^o/3p. Условие второе: необходимо пропустить по ка­тушкам равные по амплитуде и сдвинутые во времени на ∆t=T/3 или ∆ωt = 360^o/3=120^o пере­мен­ные токи (симметричный трехфазный ток). При соблюдении указанных усло­вий в про­странстве вокруг катушек будет создано круговое вращающееся маг­нитное поле с постоян­ной амплитудой индукции В_max вдоль его оси и с посто­янной угловой скоростью вращения ω_п.

На рис. 103 показано пространственное расположение трех (p = 1) одина­ковых катушек под равными углами в 120^o согласно первому условию.

По катушкам, по направлению от их начал (A, B, C) к концам (X, Y, Z) протекает сим­метричный трехфазный ток:

i_A = I_msin(t+0),

i_B = I_msin(t120⁰),

i_C = I_msin(t+120⁰).

Магнитное поле, создаваемое каждой катушкой в отдельности, пропор­ционально току катушки (B = ki), следовательно магнитные поля отдельных катушек в центре коорди­нат образуют симметричную трехфазную систему В_(t):

B_A = B_msin(t+0),

B_B = B_msin(t120⁰),

B_C = B_msin(t+120⁰).

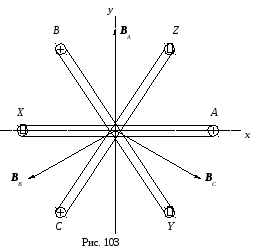
Положительные направления магнитных полей каждой катушки (векто­ров B_A, B_B, B_C) в пространстве определяются по правилу правоходового винта согласно принятым положи­тельным направлениям токов катушек (рис. 103).

Результирующий вектор индукции магнитного поля B для любого мо­мента времени может быть найден путем пространственного сложения векто­ров B_A, B_B, B_C отдельных катушек. Определим значение результирующего век­тора индукции магнитного поля B для нескольких моментов времени ωt = 0⁰; 30⁰; 60⁰. Пространственное сложение векторов вы­полним графически (рис. 104а, б, в ). Результаты расчета сведены в отдельную таблицу:

t	BA	BB	BC	B	
0	0	/2Bm	/2Bm	3/2Bm	0
30	1/2Bm	-Bm	1/2Bm	3/2Bm	300
60	/2Bm	/2Bm	0	3/2Bm	600

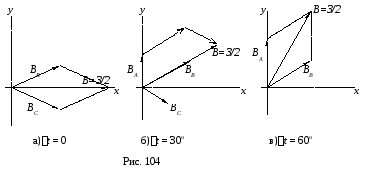
Анализ таблицы показывает, что результирующий вектор индукции маг­нитного поля имеет постоянную амплитуду (В_max=3/2B_m) и равно­мерно вращается в пространстве в положительную сторону по направлению ка­тушки А к катушке В с угловой скоростью ω_п , равной угловой частоте тока ω. В общем случае угловая скорость вращения магнитного поля зависит еще и от числа катушек:

[рад/с] или [с^-1].

В технике для характеристики вращения магнитного поля пользуются по­нятием час­тоты вращения:

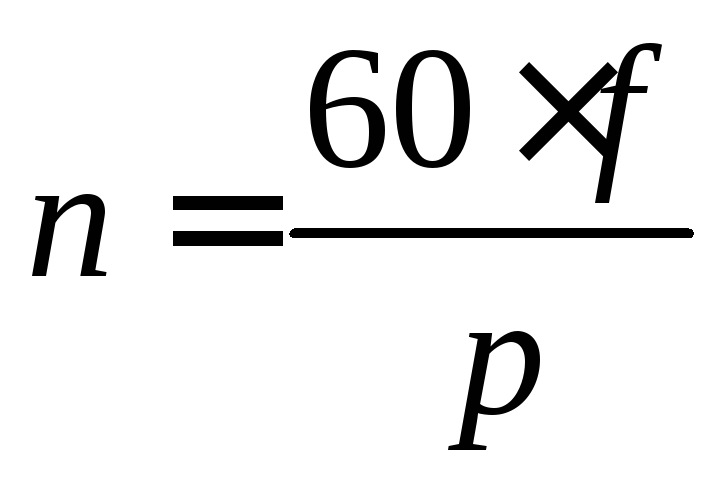[об/мин].

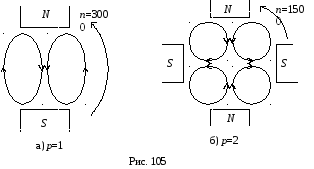
С изменением числа p пространственная картина магнитного поля изме­няется: при p=1 магнитное поле имеет два полюса (или одну пару полюсов), при p=2 – четыре полюса (или 2 пары полюсов) и т.д. (рис. 105). По этой при­чине число p = 1, 2, 3,… называют числом пар полюсов магнитного поля.

Частоту вращения магнитного поля можно изменять плавно изменением частоты пи­тающего тока f, и ступенчато - изменением числа пар полюсов p. В промышленных условиях оба способа регулирования частоты вращения поля являются технически и экономически малоэффективными. При постоянной частоте промышленного тока f=50 Гц шкала синхрон­ных частот вращения маг­нитного поля в функции числа пар полюсов выглядит следующим образом:

р, пар пол.	1	2	3	4	5	6
n, об/мин	3000	1500	1000	750	600	500

Для изменения направления вращения магнитного поля достаточно изме­нить порядок следования фаз питающего тока или, попросту, поменять местами две любые фазы источ­ника между собой.