Частотные и переходные характеристики типовых звеньев

3.6 Устойчивость сар

Анализ устойчивости непосредственно связан с определением условий равновесия. В линейных системах существуют только одно состояние равновесия. Поэтому зависимые переменные, характеризующие состояние системы, с течением времени приближаются либо к состоянию покоя, либо периодического изменения.

Если достаточно малое (независимо от того, какими причинами оно вызвано) возмущение приводит к существенному отклонению режима от исходного (установившегося) состояния или от невозмущенного движения, то говорят о нестабильности или неустойчивости положения равновесия или невозмущенного движения. Если же после прекращения действия возмущения система не отклоняется существенно от своего исходного состояния, то такой режим называют устойчивым.

Методы анализа устойчивости линейных и линеаризованных систем.

Для определения устойчивости системы с обратной связью необходимо определение всех корней ее характеристического уравнения – всех до единого. Однако в системах высокого порядка вычисление корней весьма затруднительно.

Чтобы избежать указанных трудностей и не вычислять вообще корней характеристического уравнения был разработан ряд методов, так называемых критериев устойчивости. При их помощи можно определить характер устойчивости или неустойчивости системы, не вычисляя корней характеристического уравнения.

Заметим, что частотные критерии позволяют судить об устойчивости замкнутых САР по частотным характеристикам условно разомкнутых САР без определения корней характеристического уравнения замкнутой системы. При этом необходимо знать, устойчива или нет условно разомкнутая система.

Критерий устойчивости Найквиста — Михайлова — один из способов судить об устойчивости замкнутой системы управления по амплитудно-фазовой частотной характеристике её разомкнутого состояния. Является одним из частотных критериев устойчивости. С помощью этого критерия оценить устойчивость весьма просто, без необходимости вычисления полюсов передаточной функции замкнутой системы.

Рассмотрим однокольцевую однокоординатную САР. Ее структурная схема приведена на рис.3.17:

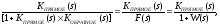(3.60)

s (или p) - оператор Лапласа (s ≡), а знак плюс в знаменателе означает, что обратная связь отрицательная. Здесь j — комплексное число, характеризующее единичный вектор, а — угловая частота.

Операторное характеристическое уравнение замкнутой системы (3.60):

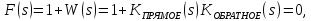(3.61)

в которое входит функция условно разомкнутой системы :

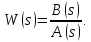(3.62)

С учетом (3.11) выражение (3.62) можно переписать

и представить в виде:

(3.63)

где q_n и r_n – корни соответственно числителя и знаменателя уравнения (3.63). В общем случае корни q_n и r_n – комплексные числа.

Корни полинома числителя называют нулями, а корни знаменателя - полюсами.

(3.64)

Для того, чтобы система САР была устойчивой необходимо и достаточно, чтобы в знаменателе выражения (3.60), (в уравнении 1+ W(s) = 0) не было корней с положительными α, т.е. расположенных в правой полуплоскости комплексной частоты s. Сказанное аналогично и для уравнения (3.64).

В теории САР Г. Найквистом в 1932 году было доказано, что

– если система устойчива в разомкнутом состоянии, то для устойчивой работы системы в замкнутом состоянии необходимо и достаточно, чтобы АФХ разомкнутой системы для не охватывала точку с координатами (– 1, j0). Только в этом случае приращение аргумента вектора будет равно нулю;

Применительно к логарифмическим ЛАХ и ЛФХ можно утверждать, что система будет устойчивой, если в области частот ω, где аргумент по абсолютному значению превышает π, модульбудет меньше единицы.

Передаточную функцию, не имеющую нулей или полюсов в правой полуплоскости s, называют функцией минимальной фазы, а систему, имеющую такую передаточную функцию – системой минимально-фазового типа. В системах минимально-фазового типа АЧХ и ФЧХ имеют взаимно однозначную зависимость. Это означает, что если известна одна из указанных характеристик (частота или фаза), то другая (фаза или частота) может быть однозначно определена расчетным путем.

Например, пусть коэффициент K_ПРЯМОЕ(s) системы, показанной на рис. 3.17, состоит из трех апериодических звеньев вида (3.34), включенных последовательно:

а коэффициент K_{ОБРАТНОЕ}(s) = β = const, причем 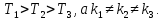Построим ЛАХ и ЛФХ для случая разомкнутой системы – отсутствияK_{ОБРАТНОЕ}(s) – рис.3.18.

В данном примере k₁ = 48дБ, k₂ = 36дБ, k₃ = 12дБ; k₀ = k₁× k₂ × k₃ = 96дБ; f₁ = 10Гц, f₂ = 1кГц, f₃ = 100кГц. Это типичная АЧХ трехкаскадного операционного усилителя без коррекции. Частота единичного усиления f₀ = 2МГц, а коэффициент усиления на постоянном токе – 96дБ.

Усилитель неустойчив, поскольку фазовый набег на частоту единичного усиления f₀ составляет φ₀ = – arctg(f₀/f₁) – arctg(f₀/f₂) – arctg(f₀/f₃) = – 90º – 87,7º – 14º = – 191,7º, а коэффициент усиления на частоте f_φ, на который фазовый сдвиг равен – 180º равен примерно +19дБ. Иными словами, для достижения границы устойчивости необходимо уменьшить фазовый набег на частоту единичного усиления f₀ на 11,7º (а с учетом запаса по фазе 30º – на 41,7º) или уменьшить коэффициент усиления на частоте f_φ на 19дБ.

Чтобы усилитель был устойчив в диапазоне эксплуатационных воздействий, необходимо обеспечить на новой частоте единичного усиления f₀ = 6кГц запас по фазе не менее 30º (фазовый сдвиг не более 150º). Если нет требований к сохранению исходной полосы пропускания, можно поступить следующим образом. Уменьшить коэффициент усиления введением низкочастотного корректирующего ПИФ и ввести компенсацию второго интегрирующего звена исходного ОУ с помощью корректирующего ПДФ. Возможный вариант коррекции приведен на рис.3.19.