3.5 Типовые звенья

В качестве типовых звеньев САР выбирают наиболее простые звенья, процессы в которых можно описать дифференциальными уравнениями не выше 2-го порядка.

      Рассмотрим типовые звенья, которые описывают дифференциальным уравнением 1-го порядка

или в операторной форме записи

(3.24)

Передаточная функция звена

(3.25)      

Для различных типовых звеньев коэффициенты принимают различные, в том числе и нулевые значения.

Различают 9 простейшие типов звеньев:

1. безынерционное (усилительное)

;

2. безынерционное с запаздыванием

;

3. инерционное (апериодическое)

;

4. интегрирующее

;

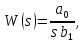
5. дифференцирующее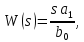

6. дифференцирующее инерционное

7. изодромное звено

8. пропорционально-интегрирующее

9. пропорционально-дифференцирующее

3.5.1 Усилительное (безынерционное) звено

Операторный коэффициент передачи

A()=W(j)= k;

() = argW(j) =

Выражения для переходной функции: Переходя к оригиналу, получим

h(t)= k1(t).

3.5.2 Усилительное звено с запаздыванием

Данное звено описывается следующим уравнением:

b_oy(t)=a_ox(t-). (3.26)

Запишем это уравнение в стандартной форме:

или (3.27)

Перейдем к операторной форме записи:

Y(s) = X(s)e^-p (3.28)

Тогда уравнение (3.28) будет иметь вид:

Y(s) = kX(s) e^-p; W(s)= ke^-p (3.29)

Найдем выражения для переходной функции.

h(t) = y(t) = kx(t-) = k1(t-) (3.30)

Переходная функция представляет собой ступенчатую функцию с амплитудой k и запаздыванием на .

Получим частотную передаточную функцию, заменив в передаточной функции (3.29) s на j:

W(s) = ke^-s

W(j) = ke^-jτ = k(cos - jsin)

W(j) = U() + jV() (3.31)

U() = kcos

V() = -ksin

Получим аналитические выражения для частотных характеристик. По определению амплитудная частотная характеристика (АЧХ) - это модуль частотной передаточной функции, т.е.

A() =W(j)= k. (3.32)

Фазовая частотная характеристика (ФЧХ) - это аргумент частотной передаточной функции, т.е.

(3.33)

3.5.3 Апериодическое (инерционное) звено

Операторный коэффициент передачи

(3.34)

Используя преобразование Лапласа

=

Переходя к оригиналу, получим

h(t) = k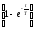1(t). (3.35)

Найдем выражение для частотной передаточной функции. Заменим в (3.34) s на j

()

Амплитудно-частотная характеристика инерционного звена

(3.36)

Фазочастотная характеристика инерционного звена

(3.37)

3.5.4 Идеальное интегрирующее звено

Данное звено описывается следующим дифференциальным уравнением:

b₁ =a_ox(t) (3.38)

Запишем это уравнение в стандартной форме:

=kx(t),

где – коэффициент передачи.

Операторный коэффициент передачи идеального интегрирующего звена

(3.39)

Найдем выражения для переходной функции

Переходя к оригиналу, получим

h(t) = kt1(t) (3.40)

Получим выражение для частотной передаточной функции.

()

Амплитудно-частотная характеристика идеального интегрирующего звена

(3.41)

Фазочастотная характеристика идеального интегрирующего звена

(3.42)