pds

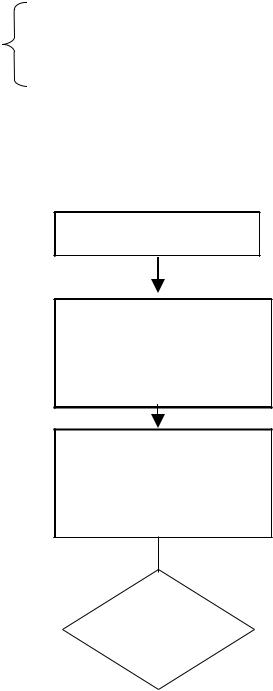
k

fn −k −i =å fn − j * hk − i − j

j= 0

0<i<n-k-1

fi − k = fi h0 + fi −1h1 +... + fi − k +1hk −1

система разностных (рекуррентных ) уравнений

fn − k = fn − 2h0 + fn − 3h1 +... + fn − k −1hk −1

Путем последовательных вычислений находим все избыт. элементы, зная hо и f

ДЕКОДИРОВАНИЕ (для обнаружения ошибок)

Прием f(x) из ДКС

Нахождение избыт. элементов f(x) по ее информационным элементам

Сравнение принятых избыточных элементов с восстановленным

нет обнаружена ошибка

СХЕМНАЯ РЕАКЦИЯ ПРОЦЕДУР КОДИРОВАНИЯ (ДЕКОДИРОВАНИЯ) ЦИКЛИЧЕСКИХ КОДОВ

а). На основе g(x)

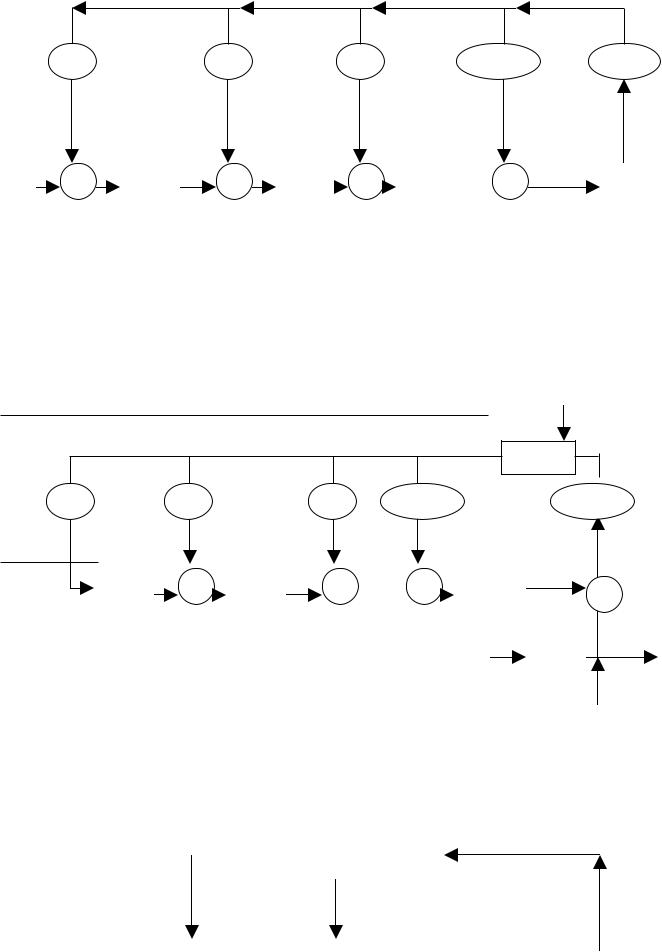
Схема деления на g(x)

Обратные связи должны соответствовать порождающим многочленам:

g(x) = g0 x0 + g1 x1 +... + gn− k xn− k

Используется в декодирующих устройствах, как схема вычисления синдрома

выход S(x)

б).На основе h(x)

Cхема расширения разностных уравнений

Общий вид:

х7 : (х³ +х+1)=х4+х2+х+1

f(x)

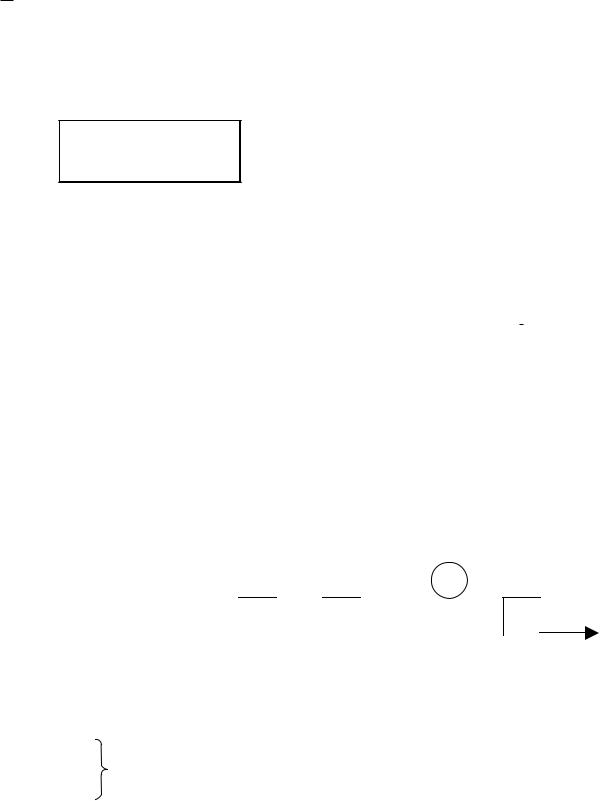
ОБНАРУЖЕНИЕ ОШИБОК

Рно= 12 n− k P( ≥d,n) не обнаруживает ошибок при S≤d-1

= ( dn )1− α p – при группировании ошибок

ИСПРАВЛЕНИЕ ОШИБОК

В кодовой комбинации n произошла t+1 ошибка

Pо.и. = P(³t +1, n)

КОДА НА ОСНОВЕ ПОСЛЕДОВАТЕЛЬНОСТИ МАКСИМАЛЬНОЙ ДЛИНЫ

Если кодируем на основе h(x) -в качестве h(x) используется неприводимый примитивный многочлен

x3 + x1 = (x +1)(x2 + x + x1) -примитивный многочлен в поле GF(22)

x7 + x1 = (x3 + x + x1)(x3 + x2 +1) GF(23)

примитивные x +15 = (x +1)(x4 + x +1)(x4 + x3 + x2 + x +1)(x4 + x3 +1)(x2 + x +1) –

Длина 7,3 информ. элемента Код (7,3) →кода (7,4) из кода Хэмминга, если проверочную матрицу сделать порождающей и наоборот

ао а1а2 а3 а4 а5 а6 ао ао а1а2 а3 а4 а5 сдвиг по фазе а5 а6 ао а1а2 а3 а4

.

.

коды, двойственные кодам Хэмминга вес кодовой комбинации один и тот же

x7 +1 g(x) = (x +1)(x3 + x +1)

d min0 d min3 = d min 4

Если будем рассматривать в качестве кодирующего устройства некоторого кода генер. Последовательность максимальной длины, то в качестве кодовой комбинации такого кода будет последовательность максимальной длины и все ее сдвиги. Такие коды могут быть построены, если в качестве h(x) выбирается неприводимый многочлен степени m, корни которого являются примитивными элементами поля GF(2m). Такие многочлены называются примитивными. В общем виде рассматриваемые коды являются двойственными для кодов Хэмминга, т.е. порождающая матрица кода Хэмминга является проверочной матрицей кода на основе ПНД, а проверочная матрица кода Хэмминга является порождающей для кода на основе ПНД. С учетом того, что в любой последовательности максимальной длины число единиц на единицу больше числа нулей, свойства рассматриваемых кодов можно выразить через число n.

n=2m-1

k=m d=2m-1

У этих кодов все кодовые комбинации имеют один и тот же весэто

эквидистантные коды ПОНЯТИЕ О МАЖОРИТАРНЫХ КОДАХ( по большинству голосов)-

-это такие коды, в которых решение по значению принятого символа кодовой комбинации принимается по большинству голосов.

h(x)=1+x+x3

ao=a1+a3 проверка 1 1 1

1 1 0

по большинству голосов→декодирование упрощается

КОДЫ РИДАСОЛОМОНА

Коды Рида-Соломона, или РС-коды, относятся к недвоичным циклическим кодам, т.е. кодам, символы которых взяты из конечного поля, содержащего q>2 элементов и обозначаемого GF(q),где q- степень некоторого простого числа.

Кодом Рида-Соломона называют циклический (N,K)-код, при N=q-1, множество кодовых комбинаций которого представляются многочленами степени N-1 и менее с коэффициентами из поля GF(q), где q>2 и является степенью простого числа, а корнями порождающего многочлена являются N- Kпоследовательных степеней: α , α2 ,α3 …αD-1,некоторого элемента α Є GF(q), где D-минимальное кодовое расстояние (N,K)-кода.

РС-код является частным случаем кода БЧХ с mo=1,тогла корни g(x) образуют ряд α ¹, α2 ,α3 …αα -1

α- примитивный элемент поля GF(q)

порождающий многочлен РСкода имеет степень N-K=D-1 и по теореме Безу может быть найден в виде произведения

g(x)=∏D− 1 (x −α i )

i= 1

n-k=d-1=2t

При фиксированных значениях N и K не существует кода, у которого минимальное кодовое расстояние больше, чем у РС-кода, у которого минимальное кодовое расстояние больше, чем у РС-кода.

Пример:

Построить код вида Соломона длины=4 с исправляющей способностью однократных ошибок t=1

t=1, dmin=3

n-K=d-1=2- связь между избыточными элементами и d g(x)=(x-2)(x-4)=x2-4x-2x-8=x2 -4x-2x-8=x2 +4x+3

порождающий многочлен

é3410ù

G(4,2) = ê ú

ë0341û

Nk=52=25 Nп=54=625

Пример из двоичного кода:

GF(23),которого строится по полю

постоим код (7,5) ←К=5 dmin=n-k+1=2+1=3

t=1 исправляет однократные ошибки g(x)=(x+α)(x+α2)=x2 + α2 x+ αx+ α3=x2+( α2+ α)x+ α3=x+ α4 x+α3 α=010

Рассмотренная процедура кодирования и декодирования для кодов вида Соломона Базируется на процедуре Быстрого декодирования кодов БЧХ Введем:

-S(x)-синхронный многочлен S(x)=f(x=αi)

вместо х корни g(x)=n-K

S(x) = S1 x0 + S2 x1 + ... + Sn − K = 2t

-многочлен локаторов ошибок:

X1 = α1 -локатор ошибок –номер разряда кодовой комбинации, где произошла ошибка

Λ(x)-многочлен локаторов ошибок=через локал. запись:

-многочлен значения ошибок Ω (х):

коэффициентом является Ylзначение в l-той позиции

локатор указывает номер позиции, а многочлензначение ошибки Потребуем, чтобы Ω(х)=S(x)*Λ (x), где S(x)-ключевое уравнение

Т.к. число избыточных элементов ограничено, делаем по модулю mod x2t

ключевое уравнение-ключ к процедуре кодирования и декодирования, т.к. по принятой комбинации принимаем S(x) и Λ(х) надо знать находим Ω(х).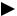 Если рассматривать комбинацию, в которой нет ошибок:

[S (x) * Λ(x)]ν2t+ 1 если рассматривать степень > ν=0 (т.к. код не может

исправлять больше, чем ν ошибок

Существует теорема:

Ω(х)= åν Yi X i Õ(1+ xX j )

i= 1

Алгоритм Форни:

Если в это выражение подствить i=l,x=X-1l

Т.е. определить выражение в точке l, то Ω(x− 1l) =Y1 Xl − 1 ∏(1 + Xl − 1 x)

АЛГОРИТМ БЫСТРОГО ДЕКОДИРОВАНИЯ КОДОВ БЧХ

Вычисление

синдрома

многочлена S(x)

ур-я относительноΛ(х)

Λ(х), а по ним определение локаторов ошибок (Хl)

значения ошибок

по теореме Форни Λ(х)-многочлен локаторов ошибок

1.Позволяет исправлять любое число ошибок (не более t),на которое способен код

2.С помощью этого алгоритма возможна процедура кодирования методом исправления стираний

3.d min = 2ν + q +1

d-1=n-k

Стертый символ=известно место, неизвестно значение

Ω(x) = S(x)Λ(x) mod x2t

МЕТОД РЕШЕНИЯ КЛЮЧЕВЫХ УРАВНЕНИЙ

Известно:S(x), кол-во ошибок ≤t

1.Составление линейных уравнений на основе ключевого уравнения и решения их(почти не применяется)

2.Алгоритм Берлскемпа-Месси

3.Алгоритм Евклида

Алгоритм Берлскемпа-Месси:

Поиск Λ(х).

В основе этого метода лежит составление схемы решения разностных уравнений путем последовательного нахождения регистра сдвига, который бы по начальным значениям компонентов синдрома многочлена генерировал все его компоненты. Методом последовательных приближений находятся связи генератора регистра сдвига и длина регистра.

S(x) = S1 x0 +... + S2 x2t − 1

Λ(x) = λ0 x0 +... + λ ν 2

Корни находятся методом перебора

Алгоритм Евклида:

a*m+b*n=d –наибольший общий делитель

Для многочленов: a(x)*m(x)+b(x)*n(x)=d(x) Приведем сумму по mod a(x):

Процесс ведут до тех пор, пока Ω(x) ≤ t-1 и находим λ(х)

СОСТАВНЫЕ КОДЫ

1.Итеративные коды (коды произведения)

2.Каскадные коды

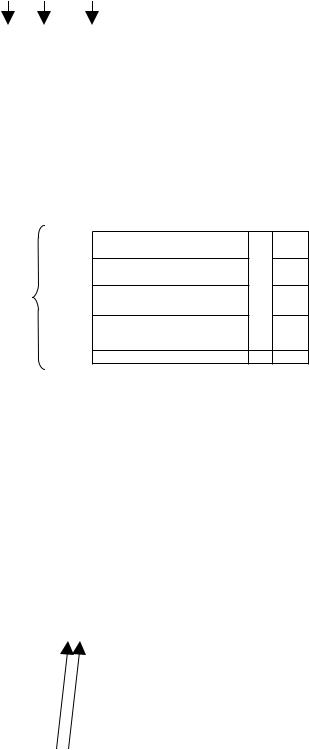
Итеративные коды:

Составляется таблица, в которую записывается кодирован.

информация. Таблица имеет К1 строк и К2 столбцов

К2 n2-K2

K1

d1

n1-K1

Получился новый код (n1*n2*K1*K2)=(nрез,Kрез) dрез=d1*d2

Матричный код (по строчкам и столбцам)-код с единственной проверкой на четность Область применения- простыми методами получить большое кодовое

расстояние (↑dmin двоичн. кодов)

Каскадные коды:

-Для исправления ошибок в больших массивах информации.

Составляется кодир. Массив в виде таблицы. Выделяются отдельные столбцы К.

каждый из столбцов рассматривается как элемент расширения поля GF(2k) Можно осуществить кодирование кодом Рида-Соломона