
pds
.pdfn-k |
n-k |
G × H T = [0] k , |
H T = [ ] k – транспонированная проверочная матрица. |
Проверочная матрица группового кода как и ПМК может быть записана в канонической форме:
H(n,k ) = [In− k R(n− k )k ` ]
G × H T = [RIk ]× [In− k R`]T = RI T n− k + Ik (R`)T = 0
R + (R`)T = 0
R`= RT
Т.о. проверочная матрица как и ПМК служит для краткого задания кода. Она задаёт код через проверочные соотношения, существующие для данного кода. Используя связь между канонической формой ПМК и проверочной матрицей мы легко по одной из них находим другую.
Дополнительные свойства проверочной матрицы.
1.Из выражения G ´ H T = 0 и из определения проверочной матрицы следует, что
произведение кодовой последовательности V на НT равно нулю.
V × H T = 0
S = V × H T - синдром ошибки, если S ¹ 0 , то есть ошибка.
S = 0 – разрешённая комбинация.
2.Умножение V на Н сводится к суммированию столбцов Н, соответствующих единицам в умножаемой комбинации. Следовательно кодовой комбинации min веса соответствует min число столбцов, в сумме дающих чисто нулевой столбец, т.е. min кодовое расстояние группового кода, равное min числу линейно зависимых столбцов в проверочной матрице.
Методы кодирования и декодирования групповых кодов.
1. Методы кодирования.

а) На основе порождающей матрицы.
Известны данные пользователя u и то, что код разделимый :
r |
|
u |
|
||
n-k |
|
k |
|
V = u× G |
(n,k ) |
= u × [R × I |
k |
] = |
|
uR |
|
+ uI |
k |
|
|
|
|
|
|
|
|
|
|||
k |
|
|
|
|
|
r избыточная часть |
|
|||
|
|
|
|
|
|
|
|
|
u |
|
Пример. |
|
é1 |
0 |
|
1 |
0 |
0ù |
|
|
|
|
|
|
|
|
|
|||||
Код (5,3), |
|
ê |
1 |
|
0 |
1 |
ú |
u = 101 |
||
G = ê1 |
|
0ú , |
||||||||
|
|
ê0 |
1 |
|
0 |
0 |
1ú |
|
|
|
|
|
ë |
|
|
|
|
û |
|
|
|
Vu = (101) ×[G(5,3) ] = |
складываем те строки в G, где в u стоят единицы. |
|||||||||
б) На основе проверочной матрицы. Известна информационная часть.
(r,u) ´ H T |
éI |
|
ù |
= r + uR = 0 |
= (r,u)ê |
n− k |
ú |
||
|
ë |
R |
û |
|
r = uR
Вывод:
Если число избыточных символов меньше, чем число информационных символов, то удобнее кодировать по способу б), иначе по а).
Пример. |
|
|
|
r1 r2 |
|
r3 r4 r5 |
||
H (5,3) |
é1 |
0 |
1 |
1 |
0ù |
r |
|
u |
= ê |
|
|
|
ú |
|
|
|
|
|
ë0 |
1 |
0 |
1 |
1û |
|
|
|
|
n-k |
|
k |
|||||
|
|
|
|
|
|
|
||
u = 101 |
|
|
|
|
|
|
|
|
r1 = u1 + u2 = 1 |
|
|
|
|
|
|||
r2 = u2 + u3 = 1 |
|
|
|
|
|
|||
V = 11101 |
|
é0 |
1ù |
|
|
|
|
|
|
|
|
|
|
|
|
||
Или |
|
|
ê |
ú |
=11 |
|
|
|
(101) ´ê1 |
1ú |
|
|
|
||||
|
|
|
ê1 |
0ú |
|
|
|
|
|
|
|
ë |
û |
|
|
|
|
2. Методы декодирования.
S = V × H T - синдром ошибки, если S ¹ 0 , то есть ошибка. Чтобы её исправить нужно привязать конкретный синдром к конкретному образцу ошибки. S – вектор из n-k. Тогда всего возможно 2n-k – значений синдрома.
Пусть передавалась кодовая комбинация V, а была принята V`. V` = V + R, где R – образец ошибки. Тогда S = V `×H T = (V + e) × H T = V × H T + e × H T . - если не совпадает с видом кодовой комбинации, иначе тоже равно нулю.
Связь между e ошибок и синдромами устанавливается с помощью таблицы декодирования (разложение группы по подгруппам на смежные классы). Таблица декодирования содержит 2n-k строк и 2k столбцов.
V0 = (00…0) |
V1 |
V2 |
… |
Vi |
… |
V2k-1 |
|||
e1 = (10…0) |
V1 |
+ e1 |
V2 |
+ e1 |
… |
Vi + e1 |
… |
V2k-1 |
+ e1 |
e2 = (010…0) |
V1 |
+ e2 |
V2 |
+ e2 |
… |
Vi + e2 |
… |
V2k-1 |
+ e2 |
|
|
2n |
e2n-k-1 |
V1 + e2n-k-1 |
V2k-1 + e2n-k-1 |
e1 = (10…0) – лидер смежного класса.
Если dmin = 3, то в эту таблицу не вошли коды веса 1 и 2. e1 ни в одном помехоустойчивом коде, т.к. dmin = 1. Будут перечислены все возможные варианты
искажений 2n и только один раз. В качестве первого столбца – комбинации min веса, не вошедшие в верхние строчки. Для каждого образца ошибки появляется свой индивидуальный синдром.
Метод максимального правдоподобия.
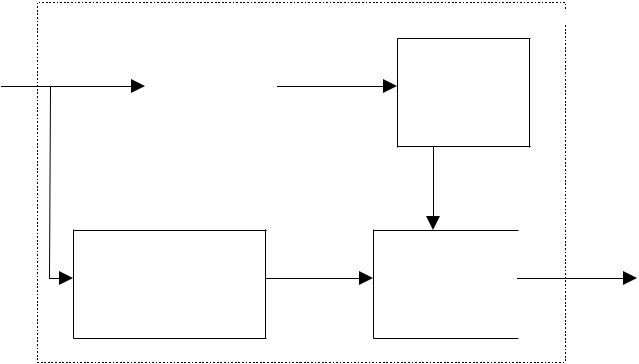
Вход декодера |
Из |
|
||
|
||||
|
|
дискретного |
Схема |
|
|
|
|
канала |
|
|
|
|
вычисления |
|
|
|
|
|
|
|
|
|
|
S |
|
|
|
|
|
Накопитель
принятой
комбинации
Всего ошибок: 2n – 2k Может исправить: 2n-k Может обнаружить: 2n – 2k
декодер 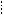
Нахождение e
Схема |
|
устранения |
Выход |
ошибок |
декодера |
|
|
Важнейшие групповые коды.
Из групповых кодов наиболее известны:
∙Коды Хемминга
∙Коды Голея
∙Коды с единственной проверкой на чётность (нечётность)
Коды Хемминга.
Код Хемминга наиболее удобно определяется через число избыточных
элементов. Пусть n-k = r, тогда n = 2r – 1, k = 2r – r – 1, dmin = 3. В качестве проверочной матрицы H Хемминг предложил использовать матрицу размером n
столбцов и n – k = r строк, у которой в качестве столбцов записаны все ненулевые r разрядные двоичные числа в упорядоченной записи.
r = |
3 |
® |
(7,4) |
ü |
|
|
r = |
4 |
® |
(15,11) |
ï |
|
|
ï |
dmin |
= 3 |
||||
r = |
5 |
® |
(31,26) |
ý |
||
ï |
|
|
||||
r = |
6 |
® |
|
ï |
|
|
(63,57)þ |
|
|
||||
“1”“2””3””4””5””6””7”
é0 |
0 |
0 |
1 |
1 |
|
1 |
1ù |
ê |
|
1 |
0 |
0 |
1 |
ú |
|
H (7,4) = ê0 1 |
1ú |
||||||
ê1 |
0 |
1 |
0 |
1 |
|
0 |
1ú |
ë |
|
|
|
|
|
|
û |
Сумма “1”, “2”, “3” = 0 |
|
dmin = 3 |
|||||
Этот код может исправлять однократные ошибки.
Таблица декодирования состоит из 2n-k строк и 2k столбцов. Синдром совпадает с номером ошибки.
Код Голея.
(23,12) dmin = 7 – двоичный код
(11,6) dmin = 5 – троичный код
Коды строго лежат на границе Хемминга:
t
n - k = log2 åcni - для двоичного кода
i= 0
t
qn− k = åcni × (q -1)i - для троичного кода
i= 0
Коды с единственной проверкой на чётность: (n , n-1).
Это коды с максимально разнесённым расстоянием:
d-1 = n-k d = n-k+1
Коды с единственной проверкой на чётность задаются с помощью проверочной матрицы:
H(n ,n-1) = [111...1], где
а) число строк равно числу проверочных элементов (=1); б) единицы на местах тех элементов, которые охвачены
проверкой (n единиц);
в) d=2, так как при сложении двух любых столбцов получаем 0. При d=2 можно только обнаруживать однократные ошибки. Никакие ошибки чётной кратности этот код обнаруживать не будет, только ошибки нечётной кратности. Следовательно, код обнаруживает половину ошибок.
Циклические коды.
Циклические коды появились в 1959 году. Для их получения применяют регистры сдвига с обратной связью.
Циклические коды -это разновидность групповых кодов. Обозначение:(n,k).
Два определения циклического кода:
1) Циклическим (n,k)-кодом называют такой групповой код, для которого справедливо: если последовательность (a0, a1, ... , an-1) принадлежит коду, то и n-последовательность вида (an-1, a0, a1, ... , an-2), полученная путём циклического сдвига элементов, указанных в комбинации, на единицу вправо, также принадлежит этому коду (циклический сдвиг делается с помощью умножения на x).
Обычно комбинации циклических кодов представляют в виде многочленов f(x), степень которых не превышает (n-1):
(a0, a1, ... , an-1) соответствует a0x0+a1x1+a2x2+…+an-1xn-1
Такое представление даёт возможность не только складывать кодовые комбинации, но и умножать и делить по соответствующим правилам для многочленов.
2)Здесь используется возможность умножения и деления. Циклическим (n
,k)-кодом называют множество многочленов степени (n-1) и менее, каждый из которых делится без остатка на некоторый многочлен g(x), степень которого равна (n-k). Этот многочлен g(x) должен быть сомножителем
(делителем) двучлена (xn+1). Многочлен называют порождающим многочленом.
Если получаем xn+1=0, то два эти определения сходятся (xn=1).
Кодовые комбинации циклического кода представляются в виде многочленов. Сложение многочленов не изменяет их степени и эквивалентно сложению векторов, поэтому множество векторов (n-1) и менее по операции сложения многочленов представляет собой группу, т.е. групповой код. Однако умножение и деление векторов изменяет их степень. Для того чтобы обеспечить замкнутость по операции умножения векторов производят умножение многочленов по модулю многочлена(x(n-1)).
В этом случае многочлен (xn+1) является нулём, также как двойка является нулём при действиях по mod2.
Понятие о кольце и поле.
Кольцо - множество элементов произвольной природы, для которых задано два действия: сложение и умножение, и по операции сложения это множество является абелевой группой, а по операции умножения выполняются следующие аксиомы:
1. Замкнутость.
a,b R, то ab=c R, где R- кольцо.
2.Операция умножения ассоциативна. a(bc)=(ab)c
3.Элементы кольца удовлетворяют дистрибутивному закону. a(b+c)= ab+ac
Роль подгруппы в группе в кольце выполняет идеал. Если элемент кольца умножить на элемент идеала, то получим идеал.
Рассмотрим множество всех целых чисел, а идеал возьмём следующим образом: выпишем все чётные числа.
... -4 |
-2 |
{0} |
2 |
4 |
6 |
8 ... |
-идеал |
(1) |
... -3 |
-1 |
{1} |
3 |
5 |
7 |
9 ... |
(mod 2) |
(2) |
|
{}-минимальные положительные элементы {1}-минимальное число, не вошедшее в идеал
Вводя действие над числами (mod2), получили два класса вычетов, следовательно, получили кольцо.
Идеал как подгруппа по операции сложения. Если умножить (2) на (1), то результаты будут во множестве (1).
... -3 |
{0} |
3 |
6 |
9 |
12 ... |
(3) |
... -2 |
{1} |
4 |
7 |
10 |
13 ... |
(mod 3) |
... -1 |
{2} |
5 |
8 |
11 |
14 ... |
|
Если 3*4 =12, а 12 по mod 3 является нулём, а ноль входит в (3). Множество классов вычетов кольца, также образуют кольцо.
Поле - множество элементов произвольной природы, для которых задано два действия: сложение и умножение и по этим действиям удовлетворяются все групповые аксиомы.
Классы вычетов кольца при действиях по модулю простого числа образуют поле.
Классы вычетов {0} и {1} по mod 2.

+ |
|
0 |
1 |
|
∙ |
|
0 |
1 |
|
|
|
||||||||
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
0 |
|
0 |
1 |
|
0 |
|
0 |
0 |
|
1 |
|
1 |
0 |
1 |
|
0 |
1 |
||
Наличие единичного элемента:
0 |
1 |
|
|
Наличие обратных элементов:
для0 |
−0 |
|
для0 |
−0 |
|
||||
для1 |
−1 |
|
для1 |
−1 |
Обратные элементы существуют только не для нулевых элементов.
По аналогии с кольцом классов вычетов целых чисел, можно построить кольцо классов вычетов многочлена по модулю многочлена (xn +1). Этих классов вычетов будет ровно 2n , если коэффициенты многочлена взяты из двоичного кода. Для этого кольца классов вычетов можно построить идеал, если взять все многочлены (классы вычетов), кратные некоторому многочлену g(x)(многочлен g(x) образует свой класс вычетов).
В теории кодирования доказывается, что если некоторый многочлен g(x) образует идеал, то он должен быть сомножителем (xn+1), а многочлен
h(x)= xn(+)1 образует нулевое пространство для этого идеала.
g x
|
Код Рида - Соломона. |
n = q-1, |
где q-основание кода. |
Если q =2, |
то получаем код, состоящий из одного элемента (n = 2-1). |
Расширенные коды: p=qm, где p-число элементов поля. Тогда при q =2: n=2m- 1 (т.е. берём не числовое поле, а поле из последовательностей нулей и единиц).
Запишем множество многочленов по mod (xn+1):
{0}, |
|
xn +1, |
x (xn +1), |
… |
{1}, |
|
xn +1+1, |
xn+1 +x+1, |
… |
{x}, |
… |
|
|
|
{x+1}, |
… |
|
|
|
{x2}, |
… |
|
|
|
{x2 +1}, |
… |
|
|
|
{x2 +x+1}, …
:
{xn-1 +xn-2 +x+1}, …
Всего получили 2n различных кодовых комбинаций. Надо из 2n кодовых комбинаций выбрать 2k< 2n .Для этого: если это множество построено по модулю многочлена f(x) и при этом этот многочлен состоит из:
f(x)=g(x)*h(x)=0, то идеал будет включать все многочлены, кратные g(x), а его размер будет k.
Можно построить идеал на основе h(x). Идеал будет кратен h(x), а его пространство будет (n-k).
Мы получили циклический код, у которого каждый многочлен кратен многочлену g(x) или h(x).
Рассмотрим поле. Хотим перейти к полю с большим основанием. Это можно сделать либо расширением (p=2m), либо увеличением основания q.
Простые и расширенные поля.
Простыми полями называют поля, сформированные по модулю простого числа (простое число делится на 1 и на себя).
Простое поле представляет собой кольцо классов вычетов по модулю простого числа с конечным числом элементов. Для конечных полей используется обозначение GF(q), где q- число элементов поля, q = p (простое число).
Для конечных полей справедливо следующее свойство: мультиплексированная группа поля Галуа является циклической. Это означает: все элементы поля могут быть получены как степени одного из элементов поля. Элемент поля, который порождает все остальные элементы, называют примитивным элементом поля.
Пример:
Есть GF(q), q=5 Элементами этого поля являются {0}
{1}
{2}
{3}
{4}
20=1
21=2
22=4
23=8 (8 по mod 5 будет 3)
Следовательно, 2 –это примитивный элемент поля.
Расширенным полем называют такое поле, элементами которого являются последовательности заданной длины, состоящие из элементов основного поля.
q = p=2 |
Þ GF(2) (элементы поля: 0 и 1) |
Как построить элементы расширенного поля? |
|
GF(qm) |
→ GF(2m) (для расширенного поля) |
Возьмём m=2: |
|
GF(2)=0,1 |
-простое поле |
GF(22)=00, 10, 01, 11 -расширенное поле (все последовательности нулей и единиц).
Обозначим многочлены:
f(x) = 00=0 f(x) =10=1 f(x) =01=x f(x) =11=x+1
Элементы расширенного поля можно получить как кольцо классов вычетов по модулю неприводимого многочлена степени m, коэффициенты которого взяты из основного поля.
Для того чтобы построить поле GF(2m), надо построить кольцо классов вычетов неприводимого многочлена (xm + … +1) с коэффициентами основного поля.
m=2 → x2 +x+1
П(a)=α2 +α+1 (вместо x подставляем α).
Строим элементы поля:
0 = |
0 |
= |
00 |
|
α0 |
= |
1 |
= |
10 |
α1 |
= |
α |
= |
01 |
α2 |
= 1+α |
= |
11 (т.к. α2 по модулю (α2 +α+1) равно 1+α) |
|
Если α0 разделить на(α2 +α+1),то остатком будет α0 (т.к. деление начнётся с α2)
Порождающие и проверочные матрицы для циклических кодов.
Циклические коды являются групповыми кодами. Множество многочленов, кратных некоторому многочлену является замкнутым. Среди кодовых комбинаций всегда есть нулевой многочлен. Таким образом, все изложенные выше способы описания групповых кодов применимы и для циклических кодов.
Порождающая матрица циклического кода строится как множество из k многочленов, кратных многочлену g(x):
