
pds
.pdf
∙Модель ВАС
∙Модель Пуртова Л.П.
∙Модель p,α
α- Показатель группирования ошибок
Задача:
Были проведены статистические исследования дискретного канала, в ходе испытания было передано N двоичных битов. Эти элементы передавались n-элементным кодом (комбинациями). При обработке экспериментальных данных было выявлено, что всего М двоичных элементов принято с ошибкой. А ошибки располагались в В кодовых комбинациях.
Определить:
1)среднюю вероятность ошибочного приема p 2)вероятность искажения кодовой комбинации P(= 1,n) f ( p) , n- длина кодовой комбинации
1) |
p = |
M |
|
|
|
|
|
N |
B nB |
|
|
2) |
P(= 1,n) = |
f ( p) |
|||
|
|||||
|
|
N / n N |
|
||
Рассмотрим два придельных случая
а) равномерное распределение ошибок в кодовой комбинации. Пусть в искаженной кодовой комбинации была всего одна ошибка, т.е. M=B.
P(= 1,n)= |
nB |
= |
nM |
np при |
M |
= p |
N |
N |
N |
б)Все ошибки в одной кодовой комбинации и все элементы этой кодовой комбинации искажены (сильное группирование ошибок).
Все ошибки в одной кодовой комбинации: B=1 Все искажены: M=n
P n 1 M
(= 1, ) = N
В результате решения задачи получили: n0 p P( 1,n) np
Обобщение: P(= 1,n) =f ( p) nβ p

|
|
Схема Бернулли ≈ (np) |
|
|
(отсутствие группирования) |
45 |
0 |
Реальное группирование |
|
|
p |
|
Сильное группирование |
|
|
|
|
n |
|
На графике двойной логарифмический масштаб.
Заменили: β = 1− α , где α - показатель группирования
α= 0 - группирование отсутствует
α= 1 - сильное группирование
Тип канала |
|
|
p |
α |
|||
Кабельные линии |
|
10-3÷10-5 (высокое) |
0,5÷0,7 |
||||
Радиорелейные линии |
10-2÷10-4 (среднее) |
0,4÷0,6 |
|||||
Радио КВ линии |
|
10-1÷10-3 (низкое) |
0,3÷0,5 |
||||
P(= 1,n) |
n1− α |
p - модель Пуртова |
|
||||
P(= m,n) |
|
n |
1− α |
p ,где m |
n |
|
|
( |
|
) |
|
|
|||
m |
3 |
|
|||||
|
|
|
|
|
|
||
Помехоустойчивое кодирование.
Основные понятия для помехоустойчивого кодирования.
Помехоустойчивое кодирование – основной метод защиты от ошибок.
Если минимальное кодовое расстояние d 2 , то такие коды называются
помехоустойчивыми.
Кодовое расстояние – степень отличия двух кодовых комбинаций (число различных элементов).
Помехоустойчивый код – код, способный обнаружить и (или) исправить ошибку в кодовой комбинации.
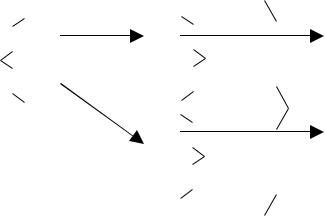
Принципы обнаружения и исправления ошибок (на примере блочных кодов).
1) Обнаружения ошибок
NÏ - полное множество кодовых комбинаций длины n. Если используем для передачи NÊ < NÏ
NÊ - разрешенные комбинации для передачи
NÏ − NÊ - запрещенные комбинации
Ограничение числа кодовых комбинаций для передачи :
передатчик
|
|
|
|
|
|
|
|
Правильный прием или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Nк |
|
|
|
|
|
|
|
прием с необнаруженной |
|
|
|
|
|
Nк |
|
ошибкой |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
Nп |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
Nп- Nк |
|
ошибки |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ошибка выявляется, когда передаем разрешенную, а принимаем запрещенную комбинацию. Но не можем обнаружить, если была предана одна разрешенная комбинация, а принята другая разрешенная комбинация.
Отношение числа обнаруженных ошибок к общему числу возможных
ошибок : μî áí = |
NÊ −(NÏ |
NÊ ) |
=1− |
NÊ |
- эффективность обнаружения |
NÊ NÏ |
|
|
|||
|
|
|
NÏ |
||
2) Исправление ошибок
Не достаточно выделять защитную зону NÏ − NÊ . Для каждой кодовой
комбинации своя защитная зона. Эффективность исправления ошибок:
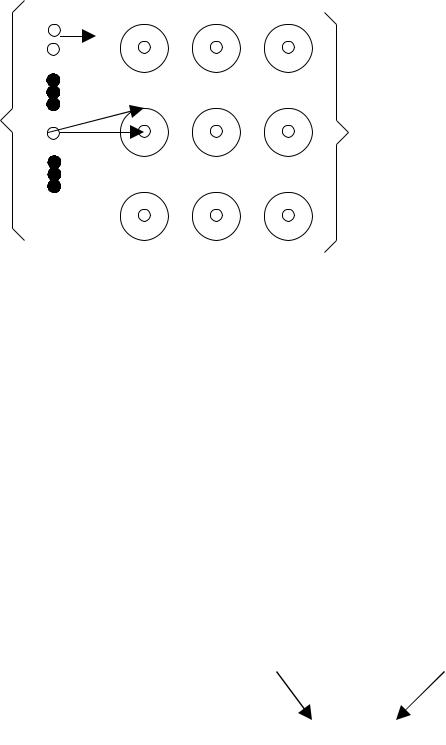
|
|
|
|
|
Непересекающиеся |
|
V1 |
|
|
|
защитные зоны для |
||
V1 |
V2 |
V3 |
каждой кодовой |
|||
V |
|
|||||
2 |
комбинации |
|||||
|
|
|
|
|||
NÏ |
Vi |
NÏ |
|
||
Vi |
Vi |
VL
Эффективность исправления ошибок:
|
NÊ |
NÏ |
− NÊ |
|
|
|
|
NÊ |
ηèñï ð = |
|
NÊ |
|
= |
1 |
1− |
||
|
|
|
||||||
NÊ |
NÏ |
|
NÊ |
NÏ |
||||
|
|
|
|
|||||
Доля исправляемых ошибок трансформаций в NÊ раз меньше, чем доля обнаруженных. (Исправление ошибок а NÊ раз менее эффективно). Его
используют, а в том случае, когда отсутствует канал обратной связи между передатчиком и источником, т.е. передача информации происходит в одном направлении.
Основные характеристики помехоустойчивых кодов.
1.Избыточность
NÊ < NÏ (только в этом случае |
Избыточные |
|
|
|||
код способен обнаружить и |
|
|
||||
(проверочные) |
Информационные |
|||||
исправить ошибку). |
||||||
элементы |
|
элементы |
||||
Есть кодовая комбинация. Как |
|
|||||
|
|
|
|
|
||
эти требования |
|
|
|
|
|
|
трансформируются на каждую |
|
|
|
|
|
|
|
n-k |
|
k |
|
||
кодовую комбинацию? |
|
|
|
|||
|
|
|
|
|
||
|
m |
NÊ |
||||
n = log2 NÏ |
|
|||||
|
|
|
|
|
||
Сколько из n элементов используется для передачи информации?
ê = log2 NÊ
В пределах каждой кодовой комбинации выделим ê элементов, в которой передаем информацию.
Чтобы передать коду помехоустойчивые свойства: n − k = m
Проверочные элементы используются для проверки принадлежности данной комбинации к используемому коду.
2.Минимально кодовое расстояние dmin 2 (для избыточных кодов)
3.Кратность гарантийно исправляемых ошибок (t)
Гарантийно – если t=2 , то исправляются все варианты ошибок (однократные и двукратные) – исправляются все ошибки всех кратностей до t включительно.
Больше t – уже не гарантийно (может исправлять, а может и нет).
Связь между t и dmin :
dmin + 2t 1 |
1 |
|
Запрещенные |
|
t |
t |
комбинации |
|
|
||
|
t |
t |
|
|
dmin |
|
|
4.Кратность гарантийно обнаруженных ошибок (s)
Гарантийная кратность – все варианты ошибок код обнаруживает.
Связь между dmin и s :
s должно быть таким, чтобы оно не переводило одну комбинацию в другую (отличие хотя бы на 1). Выделим зону радиуса s и сделаем так, чтобы в этой зоне крайняя точка любой разрешенной комбинации отличалась хотя бы на 1 символ от
другой. dmin + s 1
1
Vк 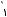 dmin
dmin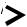 Vi
Vi 
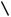 Запрещенные комбинации
Запрещенные комбинации
k
5. n - скорость кода (коэффициент кода)
Граничные соотношения между характеристиками помехоустойчивого кода.
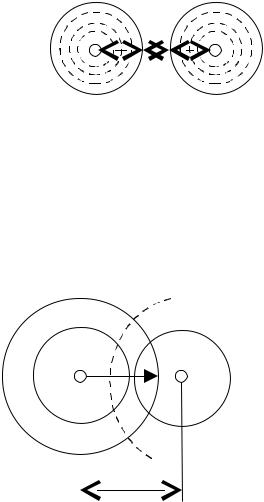
I. Граница Хемминга.
Сколько в этой зоне запрещенных + 1 кодовых комбинаций?
t |
Cni |
|
Vi t 1 t |
2n = 2k |
|
|
|
i= 0 |
|
|
|
Разделим на |
2k |
и прологарифмируем: |
|
n − k log2 |
t |
Cni Граница Хемминга(граница плотной упаковки сферы) |
|
|
i= |
0 |
|
Коды на границе Хемминга и есть сами коды Хемминга.
II. Граница Варшамова – Гилберта
2n = 2k d − 1 Cni |
Vi dmin − 1 Vi |
|
i= 0 |
||
Разделим на 2k и прологарефмируем: |
|
|
|
|
|
n − k log2 d − 1 Cni |
|
|
i= 0 |
|
dmin |
упрощенное выражение для границы |
|
|
Варшавова - Гилберта |
|
|
|
|
|
Таких кодов значительно больше, чем кодов, удовлетворяющих границы Хемминга, и эти коды хорошие.
III. Граница максимально разнесенных кодов (максимальная граница)
dmin = n − k +1
Устанавливает максимальное значение dmin для определенной избыточности.
Таких кодов мало: коды с проверкой на четность и другие. Ее открыл Синглтон (граница Синглтона).
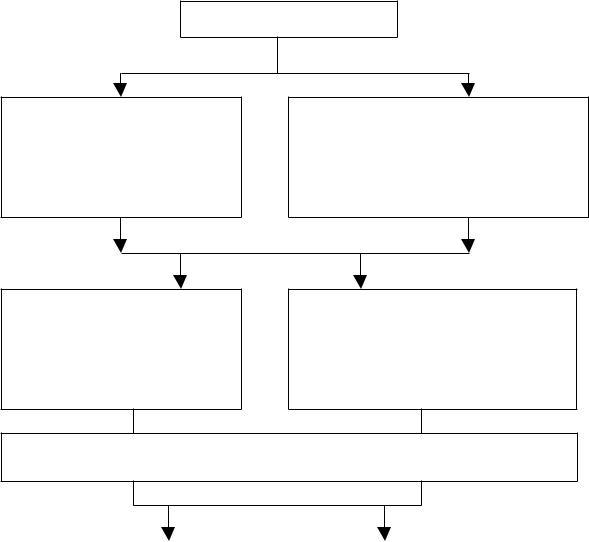
Классификация помехоустойчивых кодов.
Помехоустойчивые коды
Боковые
(связи между элементами информации и избыточными ограничены длиной )
Разделенные
(если в кодовой комбинации можно указать, какие комбинации являются информационными, а какие избыточные )
Непрерывные
(связи между элементами информации и избыточными распределены по всему сообщению. Все сообщения представляют собой одну кодовую комбинацию )
Разделенные
(если в кодовой комбинации нельзя указать, какие комбинации являются информационными, а какие избыточные. Их число известно а место не известно. )
Если помехоустойчивый код создается на основе некоторой математической системы, то это систематический код
Систематически |
|
Систематически |
(наиболее яркие представители: |
|
|
|
(если групповой код не |
|
линейные (групповые) коды. |
|
|
|
систематический, то он неразделимый. |
|
Используются линейно- |
|
|
|
Пример: код с постоянным |
|
векторные пространства, |
|
|
|
соотношением 1 и 0 ) |
|
системы линейных уравнений) |
|
|
|
|
|
|
|
|
Групповые коды.
Определение группы и её свойства.
Блоковые коды – характеризуются длиной кодовой комбинации n (n- последовательность).
Действия над кодовыми комбинациями – поразрядное сложение Å (по mod2)/ Группа – одна из основных систем, рассматриваемых в высшей математике.
Группой (G) называется множество элементов произвольной природы, для которых задано одно из действий (либо сложение, либо умножение). И по этому действию (операции) это множество обладает следующими свойствами (удовлетворяют следующим аксиомам):
1. Замкнутость.
Рассмотрим на примере сложения (для умножения тоже самое).
a,b G
a+b = c, c ÎG
2.Ассоциативность (сочетательность).
a+ (b + c) = (a + b) + c
3.Наличие единичного элемента.
Среди элементов группы есть единственный элемент l, такой что для любого элемента группы a выполняется соотношение: a + l = l + a = a
+ 10101
Например, 00000
10101
4. Наличие обратных элементов.
Для каждого элемента a группы в группе есть обратный элемент a , такой что a + a = a + a = e
5. Коммутативность.
Если a и b элементы группы и не важен порядок, т.е. a +b = b + a, то такая группа называется коммутативной или абелевой.
Группа называется конечной, если она состоит из конечного числа элементов. В противном случае она называется бесконечной.
Пример.
Задав в качестве групповой операции операцию сложения по mod2, убедимся, что множество 000, 001, 010, 100, 110, 011, 101, 111 является группой. Складывая элементы множества в различном сочетании, видим, что каждый раз получаем элемент, входящий в множество. Так, 001Å100 = 101 и т.п. Легко заметить, что условие ассоциативности также выполняется. Единичным является элемент 000. Для каждого элемента, заданного в примере множества, существует обратный. Так, для элемента 100 обратным является он сам, т.е. 100 Å100 = 000 . Таким образом, рассматриваемое множество является группой, порядок которой (число элементов) равен восьми. Видно также, что данная группа является коммутативной.
Групповым кодом называется множество n-последовательностей, которые являются абелевой группой по введённой операции поразрядного сложения Å.
Для групповых кодов принято обозначение (n,k) – код (k – число информационных элементов, n – общее число элементов).
Свойства групповых кодов.
1.Групповой (линейный) код является подгруппой множества всех последовательностей длины n. (А множество всех последовательностей длины n называется группой).

Для того, чтобы множество из n-последовательности из общего числа всех последовательностей длины n было группой, достаточно проверить наличие единичного элемента (нулевого) и замкнутость.
2. Min кодовое расстояние группового кода равно весу его ненулевых комбинаций.
Это свойство обусловлено тем, что сумма любых комбинаций группового кода также является кодовой комбинацией, а значит комбинация min веса указывает на степень удалённости комбинаций данного кода.
Любой групповой код не обнаруживает только те ошибки, которые по своему виду совпадают с видом кодовой комбинации.
Способы задания групповых кодов.
a0, a1, a2, a3, … an-1 – последовательность длины n.
a0 × e0 + a1 × e1 + + an− 1 × en− 1 - вектор n-мерного пространства ( ai - скаляр, ei - орт).
NП ~ VП
NК ~ VК
1.Базис – совокупность линейно независимых векторов, с помощью которых можно получить все вектора, входящие в это пространство.
2.Линейная комбинация кодовой комбинации.
W= c0 ×V0 + c1 ×V1 + c2 ×V2 + + ck ×Vk
3.Линейная зависимость и линейная независимость. (Линейная независимость: W = 0, когда все сi = 0)
Способы задания.
1.По аналогии с линейным векторным пространством можно задавать групповые коды с помощью базиса подпространства размерности k n-мерного векторного пространства. [Порождающая матрица кода (ПМК)]
Строками этой таблицы являются k линейно независимых кодовых комбинаций. ПМК обозначается: (), 


 , [].
, [].
n
G(n,k) = |
|
k |
|
Пример.
Пусть в групповом (5,3) коде связи между информационными и избыточными элементами задаются с помощью следующих линейных отношений:
Элементы комбинаций кода a0, a1, a2, a3, a4, где a2, a3, a4 - информационные, а a0, a1 – избыточные элементы. Избыточные элементы могут быть получены путём суммирования по mod2 определённых информационных элементов. Т.о. a0 = a2 Å a3 ,
a1 = a3 Å a4 .
00 000
10100
11010
01110
01001
11101
10011
00111
Первые два столбца – это избыточные элементы, полученные путём суммирования по mod2 определённых информационных элементов, а оставшиеся три столбца – информационные элементы. Исходя из этого можно построить ПМК:
RI
é1 |
0 |
1 |
0 |
0ù |
|
ê1 |
1 |
0 |
1 |
0ú |
= G |
ê |
1 |
0 |
0 |
ú |
|
ê0 |
1ú |
|
|||
ë |
|
|
|
û |
|
ПМК – служит для краткого задания кода. Для однозначности задания кода с помощью порождающей матрицы вводится понятие канонической формы порождающей матрицы:
n
G(n,k ) = [Rk (n− k ) I k ] k
2. Проверочная матрица группового кода (Н). Свойство.
Если два вектора по скалярному произведению равны нулю, то они ортогональны.
Смотри предыдущий пример. a0, a1, a2, a3, a4
a0 = a2 Å a3 |
« a0 Å a2 Å a3 |
= 0 |
« |
|||
a1 = a3 Å a4 |
« a1 Å a3 Å a4 |
= 0 |
« |
|||
|
|
R` |
|
|
|
|
é1 |
0 |
1 |
1 |
0ù |
|
|
« ê |
1 |
0 |
1 |
ú - базис нулевого пространства (5,3) кода. |
||
ë0 |
1û |
|
|
|||
Проверочные
вектора
W = 1×1+ 0 × 0 +1×1+ 0 ×1+ 0 × 0 = 1+ 0 +1+ 0 + 0 = 0
H – базис нулевого пространства (n,k) кода.
H =[n ] n −k в качестве строк – проверочные вектора данного кода.
