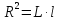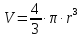2. Метод групповых инкрементов по Аскадскому а.А

В этой работе для расчета термодинамических характеристик полимеров используется метод инкрементов [10]. Сущность его заключается в следующем. Выбирается повторяющееся звено полимера, и каждый атом его окружается сферой, равной его Ван-дер-Ваальсовому радиусу. Ван-дер-Ваальсовые радиусы атомов R_i (где i-соответствующий химический символ атома) берутся из рентгеноструктурных данных. Тогда Ван-дер-Ваальсовый объем атома можно определить как ту часть объема усеченной сферы, которая остается после пересечения сферы радиуса R_c сферами радиуса R_н, расположенными на расстоянии длин химической связи.

Физический смысл Ван-дер-Ваальсового объема атома его деформация (изменение объема) за счет химических связей, а физический смысл Ван-дер-Ваальсового объема повторяющегося звена - это собственно объем звена, занимаемый в полимере в случае плотной упаковки, поскольку Ван-дер-Ваальсовые радиусы соответствуют равновесному положению атомов звена относительно повторяющихся звеньев данной макромолекулы или собственных макромолекул.

Пусть нам надо определить какую - то величину Q (в качестве Q может быть величина, обратная температуре плавления, температуре стеклования, плотности упаковки и т.д.) для полимера с заданным химическим строением повторяющегося звена. Тогда согласно методу инкрементов [10]:

(3)

где Q_i-вклад i-го атома в величину Q.

Величина Q_i будет зависеть соответствующим образом от энергии взаимодействия D_i атома i-го типа. В общем виде эту зависимость можно записать: Q_i=ƒ_i(D_i). Если мы рассматриваем плавление полимера или вклад в коэффициент объемного расширения, тогда в качестве D_i будет выступать энергия Ван-дер-Ваальсового взаимодействия. Если нас интересует температура деструкции, то в качестве D_i необходимо рассматривать энергию химической связи. Однако этим не ограничивается вклад Q_i в Q. На ряду с указанными выше взаимодействующие группы атомов могут образовывать новый тип взаимодействий, которые существенно влияют на термодинамические свойства полимеров. Так, группы -ОН, -NHCO- и др. образуют водородные связи, a -C≡N, -Cl, -COO- и др. приводят к возникновению сильного диполь-дипольного взаимодействия. Кроме того, на термодинамические свойства может влиять надмолекулярная структура и т.д. Однако последний фактор мы будем пренебрегать, так как точность метода (≤5%).

Таким образом, наряду с Ван-дер-Ваальсовыми и химическими связями необходимо учитывать водородные связи и диполь-дипольные взаимодействия.

Кажущаяся простота определения критических температур методом инкрементов в сочетании с ясным физическим смыслом входящих в него параметров в некоторых случаях породили у ряда исследователей мысль распространить аддитивную схему как модуль упругости. В результате, чтобы такие аддитивные схемы действовали также успешно, потребовалось ведение дополнительных инкрементов, что соответственно снижает универсальность предлагаемого метода.

2. Расчет геометрических характеристик молекулярной цепи поли-1-(триметилсилил)пропина-1

   1. Контурная длина макромолекулы

Контурная длина () соответствует длине полностью растянутой макромолекулы.– это произведение длины звена мономера на степень полимеризации.

(4)

где N – степень полимеризации:

(5)

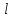–длина мономерного звена. Для ее расчета необходимо учитывать гибридизационный атом углерода и его пространственное расположение.

Найдем длину элементарного звена полимера:

Рассмотрим ∆АВС: АС=1,54 нм; СВ= 1,34 нм; угол ﮮАСВ =118,6˚;

АB===

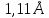Длина элементарного звена будет: =АВ =

2. Среднеквадратичный радиус клубка макромолекулы

Радиус полимерного клубка – это радиус-вектор, который описывает размер всего полимера.

(6)

где – контурная длина полимера, м;

–длина элементарного звена, м

3. Радиус полимерного клубка

4. Объем Гауссова клубка

(7)

5. Критическая концентрация

Концентрация, при которой гауссовы клубки начинают закручиваться друг с другом, называется критической концентрацией раствора.

(8)

где 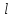– длина элементарного звена, м;

–степень полимеризации

6. Плотность полимера

(9)

где – средний коэффициент молекулярной упаковки полимера;

–молярная масса мономера, г/моль;

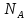–число Авогадро, моль^-1;

–Ван-дер-Ваальсовый объем повторяющегося звена, см³

7. Момент инерции

Момент инерции – это мера инертности тела при его вращении относительно неподвижной оси.

(10)

где m – масса полимера (гауссова клубка), кг;

R – радиус полимерного клубка, м

8. Молярный момент инерции

(11)

где - средняя молекулярная масса полимера,

N_A – число Авогадро

3. Расчет физико-химических свойств поли-1-(триметилсилил)пропина-1

   1. Расчет Ван-дер-Ваальсовых объемов

Основной принцип метода инкрементов:

• Выбирается повторяющееся звено полимера и каждый его атом окружается сферой, равной Ван-дер-Ваальсовому радиусу.

• Физический смысл Ван-дер-Ваальсового объема атома: деформация (изменение объема атома) за счет химических связей;

• Физический смысл Ван-дер-Ваальсового объема повторяющегося звена: собственный объем звена, занимаемый в полимере в случае плотной упаковки [9, 10].

Рис.2. Мономер поли-1-(триметилсилил)пропин-1, смоделированный cпомощью программыChemCraft.

Расчет Ван-дер-Ваальсовых объемов

(12)

где R – Ван-дер-Ваальсовый («межмолекулярный») радиус рассматриваемого атома;

h_i – высота сегмента, которая вычисляется по формуле:

(13)

здесь d_i – длины связей между двумя атомами;

R_i – Ван-дер-Ваальсовые радиусы соседних с рассматриваемыми, валентно-связанных атомов [10].

Тогда Ван-дер-Ваальсовые объемы равны:

Рис. 2. Поли-1-(триметилсилил)пропин-1 с указанием инкрементов объемов различных атомов.

ΔV_C,13 = 17,2 ų; ΔV_C,15 = 9 Å; ΔV_C,24 = 6,2 Å; ΔV_C,106 = 16,0 Å; ΔV_Si,170 = 20,3 Å; ΔV_H,124 = 2,0 ų

Сумма Ван-дер-Ваальсовых объемов:

ΣΔV_i = ΔV_C,13 + ΔV_C,15 + ΔV_C,24 + 3 ∙ ΔV_C,106 + ΔV_Si,170 + 12 ∙ ΔV_H,124

ΣΔV_i = 124,7 ų