- •Федеральное государственное образовательное бюджетное
- •1 Линейное программирование
- •Контрольные вопросы и упражнения
- •2 Различные формы записи задач линейного программирования. Приведение задачи к каноническому виду
- •3 Графический метод решения злп
- •Контрольные вопросы и упражнения
- •4 Симплекс-метод решения задач линейного программирования с естественным базисом
- •Контрольные вопросы и упражнения
- •5 Симплекс-метод с искусственным базисом
- •Контрольные вопросы и упражнения
- •6 Двойственность в линейном программировании
- •Контрольные вопросы и упражнения
- •7 Технология решения задач линейного программирования с помощью надстройки поиск решения в среде excel
- •Список литературы
- •Задания для самостоятельной работы
3 Графический метод решения злп
Наиболее простым и наглядным методом решения ЗЛП является графический метод. Он применяется для решения задач с двумя переменными, заданными в неканонической форме, и многими переменными в канонической форме при условии, что они содержат не более двух свободных переменных.
Рассмотрим задачу с двумя переменными
|
|
(1) |
|
|
(2) |
Графический метод основывается на возможности графического изображения области допустимых решений и нахождения среди них оптимального.
Геометрически
каждое ограничение
![]() системы (2) представляет собой полуплоскость
с граничной прямой
системы (2) представляет собой полуплоскость
с граничной прямой![]() .
Для того, чтобы определить, какая из
двух полуплоскостей является областью
решения, достаточно координаты какой-либо
точки, не лежащей на прямой, подставить
в неравенство: если оно верное, то
областью решения является та полуплоскость,
откуда взята точка, если неверное, то
полуплоскость, не содержащая точку.
Условия неотрицательности определяют
полуплоскости с граничными прямыми
.
Для того, чтобы определить, какая из
двух полуплоскостей является областью
решения, достаточно координаты какой-либо
точки, не лежащей на прямой, подставить
в неравенство: если оно верное, то
областью решения является та полуплоскость,
откуда взята точка, если неверное, то
полуплоскость, не содержащая точку.
Условия неотрицательности определяют
полуплоскости с граничными прямыми![]() .
Если система (2) совместна (имеет решение),
то полуплоскости, пересекаясь, образуют
общую часть, которая является выпуклым
множеством и представляет собой
совокупность точек, координаты каждой
из которых являются решением данной
системы ограничений (2). Совокупность
этих точек называетсямногоугольником
решений.
.
Если система (2) совместна (имеет решение),
то полуплоскости, пересекаясь, образуют
общую часть, которая является выпуклым
множеством и представляет собой
совокупность точек, координаты каждой
из которых являются решением данной
системы ограничений (2). Совокупность
этих точек называетсямногоугольником
решений.
Возможны следующие варианты области допустимых решений:



x1
|
а) ОДР – замкнутое множество (многоугольник) |
б) ОДР – открытое множество |
в) ОДР – пустое множество (Система ограничений не совместна) |
Рисунок 1 – Виды области допустимых решений (ОДР)
Многоугольник
решений также может быть и точкой, и
отрезком, и лучом. Для нахождения среди
допустимых решений оптимального решения
используют опорную прямую и линии
уровня. Линией уровня называется прямая,
на которой целевая функция принимает
постоянное значение
![]() ,
а опорная прямая – линия уровня, которая
имеет хотя бы одну общую точку с областью
допустимых решений и по отношению к
которой эта область находится в одной
из полуплоскостей. ОДР имеет не более
двух опорных прямых. Изменение значения
целевой функции
,
а опорная прямая – линия уровня, которая
имеет хотя бы одну общую точку с областью
допустимых решений и по отношению к
которой эта область находится в одной
из полуплоскостей. ОДР имеет не более
двух опорных прямых. Изменение значения
целевой функции![]() идет по направлению вектора
идет по направлению вектора![]() .
.
Алгоритм графического решения ЗЛП с двумя переменными:
Строят ОДР как пересечение m полуплоскостей.
Если ОДР не пустое множество, то определяют направление возрастания (убывания) целевой функции Z, т.е. строят вектор
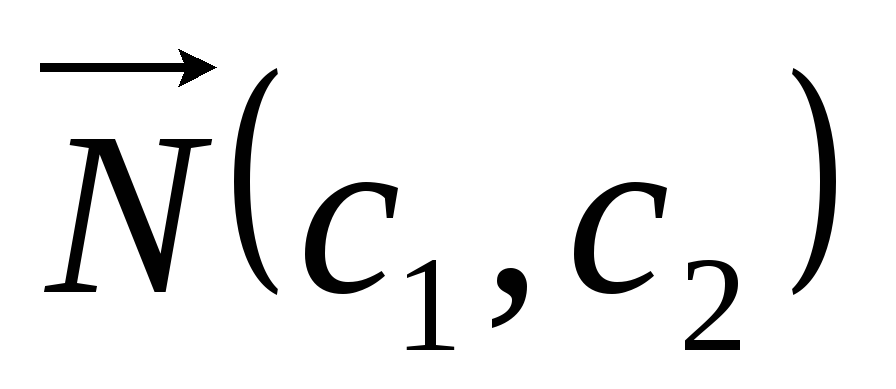 .
.Строят линию уровня
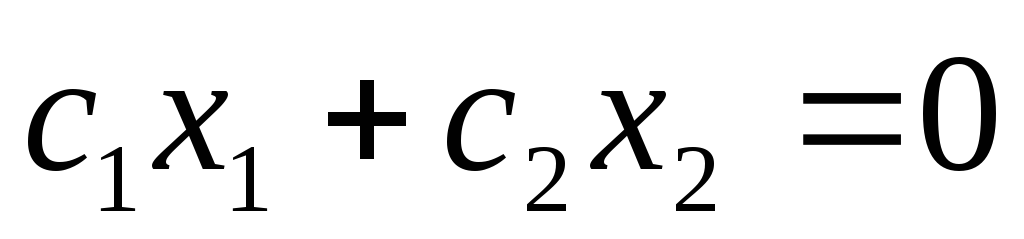 ,
перпендикулярную вектору
,
перпендикулярную вектору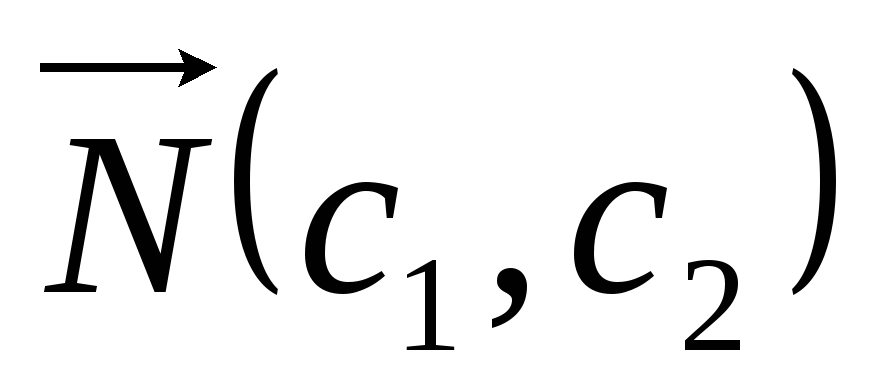 .
.Линию уровня перемещают в направлении вектора, в случае максимизации функции, или в противоположном направлении, в случае минимизации до тех пор, пока она не станет опорной прямой. Находят значение целевой функции в полученных точках или определяют, что значение целевой функции неограниченно.
Рассматриваются различные расположения опорной прямой по отношению к ОДР:



x1
|
а) Min Z в () A Max Z в () B |
б) Min Z в () A Max Z = ∞ |
в) Min Z в любой () отрезка AB Max Z в () C |
Рисунок 2 – Расположение опорной прямой относительно ОДР
Пример: Решить графически ЗЛП:
![]()

Решение:
Сначала
проведем оси: на горизонтальной будем
откладывать значения переменной x1
, а на вертикальной x2
. Далее
рассмотрим условия неотрицательности
переменных
![]() .
Эти два ограничения показывают, что ОДР
будет находиться в 1-ой четверти. Чтобы
учесть оставшиеся ограничения, заменим
неравенства на равенства, а затем на
плоскости проведем эти прямые. Например,
неравенство
.
Эти два ограничения показывают, что ОДР
будет находиться в 1-ой четверти. Чтобы
учесть оставшиеся ограничения, заменим
неравенства на равенства, а затем на
плоскости проведем эти прямые. Например,
неравенство![]() заменяем на равенство
заменяем на равенство![]() ,
которое проходит через точки (0; 2) и (-2;
0). Обозначим эту прямую 1 . Определим
полуплоскость, выбрав контрольную точку
(0; 0). Так как
,
которое проходит через точки (0; 2) и (-2;
0). Обозначим эту прямую 1 . Определим
полуплоскость, выбрав контрольную точку
(0; 0). Так как![]() - верное неравенство, то точки полуплоскости,
содержащей (0; 0) удовлетворяют первому
ограничению. Аналогично рассматриваем
оставшиеся ограничения.
- верное неравенство, то точки полуплоскости,
содержащей (0; 0) удовлетворяют первому
ограничению. Аналогично рассматриваем
оставшиеся ограничения.


![]()
|
X1 |
0 |
-2 |
|
X2 |
2 |
0 |
![]()
|
X1 |
0 |
2 |
|
X2 |
-3 |
0 |
![]()
|
X1 |
0 |
1 |
|
X2 |
2 |
0 |
Рисунок 3 – Иллюстрация решения задачи
П олучена
область допустимых решений – многоугольникABCDE.
Строим вектор
олучена
область допустимых решений – многоугольникABCDE.
Строим вектор
![]() и
линию уровня
и
линию уровня![]() .
Перемещаем линию уровня вдоль вектора
.
Перемещаем линию уровня вдоль вектора![]() до опорной прямой (обозначены пунктирными
линиями). Эта прямая проходит через
точки А и С, причем в точке А определяетсяMin
Z,
а в точке С - Max
Z.
Определим координаты точки A
как пересечение прямой 3 и прямой
x2=0:
до опорной прямой (обозначены пунктирными
линиями). Эта прямая проходит через
точки А и С, причем в точке А определяетсяMin
Z,
а в точке С - Max
Z.
Определим координаты точки A
как пересечение прямой 3 и прямой
x2=0:
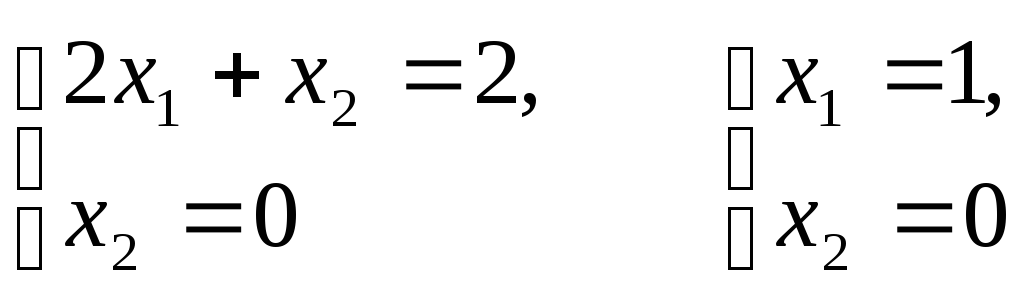 Значит,
Значит,
![]()
О
 пределим
координаты точки С как пересечение
прямых 2 и 4 :
пределим
координаты точки С как пересечение
прямых 2 и 4 :
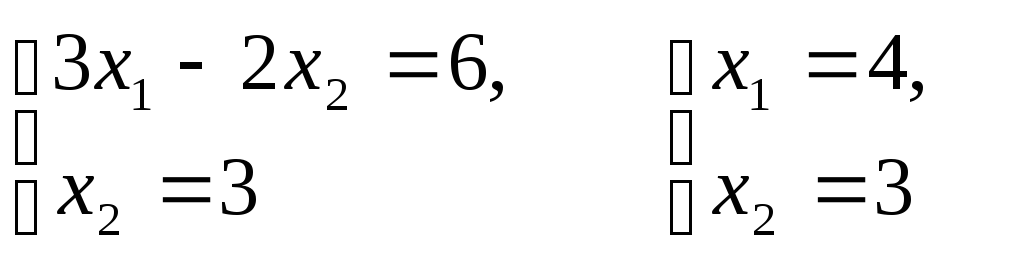 Значит,
Значит,
![]()
Графическим методом
решаются задачи линейного программирования,
записанные в каноническом виде и
удовлетворяющие условию
![]() ,
где n
– число неизвестных системы ограничений;
r
– ранг системы векторов условий. Если
уравнения системы ограничений линейно
независимы, то ранг r
равен числу уравнений системы m.
,
где n
– число неизвестных системы ограничений;
r
– ранг системы векторов условий. Если
уравнения системы ограничений линейно
независимы, то ранг r
равен числу уравнений системы m.
Пример: Решить задачу линейного программирования
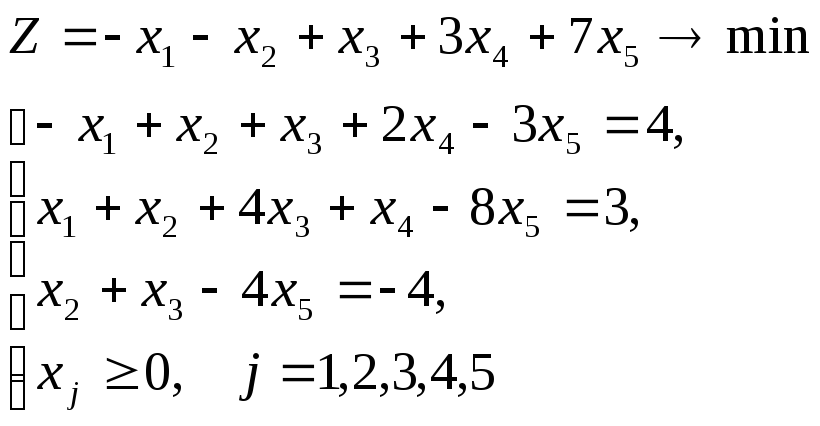
Р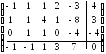 ешение:
Метод применим, так как
ешение:
Метод применим, так как
![]() .
Выпишем расширенную матрицу системы
ограничений, добавив строку, содержащую
коэффициенты целевой функции:
.
Выпишем расширенную матрицу системы
ограничений, добавив строку, содержащую
коэффициенты целевой функции:
Методом Жордана - Гаусса приведем систему уравнений – ограничений к равносильной разрешенной, одновременно исключив разрешенные неизвестные из целевой функции:

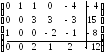
![]()
![]()
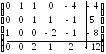
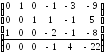

![]()
Запишем задачу в преобразованном виде:

Отбросим в уравнениях неотрицательные разрешенные неизвестные х1, х2, х3 и заменим знак равенства знаками неравенства « ≤ », получим вспомогательную задачу линейного программирования с двумя переменными
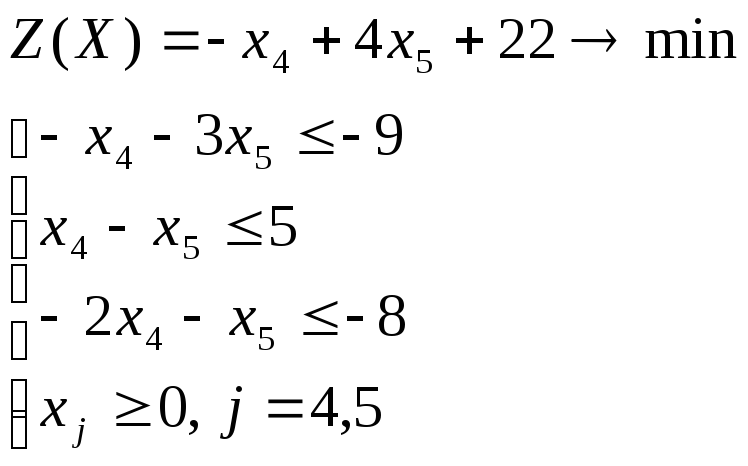
Решим задачу графическим методом. Свободный член в целевой функции 22 на отыскание оптимального решения не влияет и учитывается только при вычислении значения целевой функции.
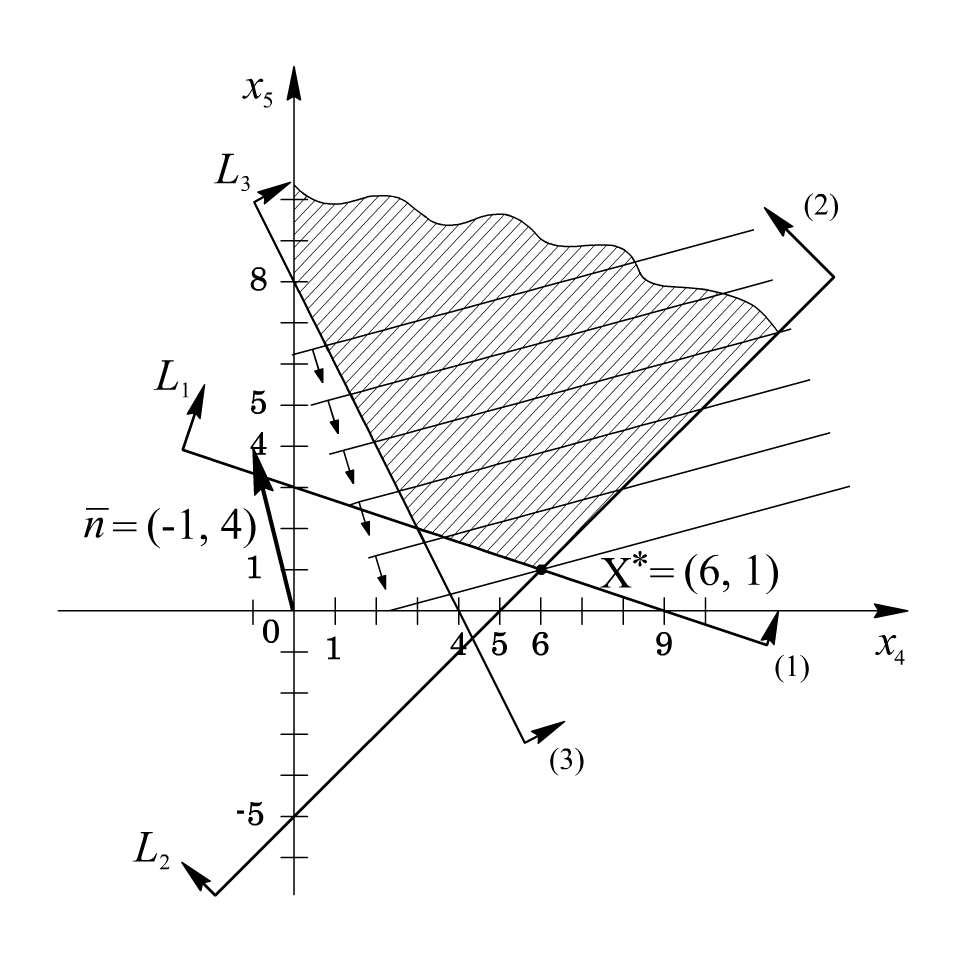
Рисунок 4 – Графическая иллюстрация решения задачи
Находим оптимальное
решение вспомогательной задачи
![]()
![]() :
:
+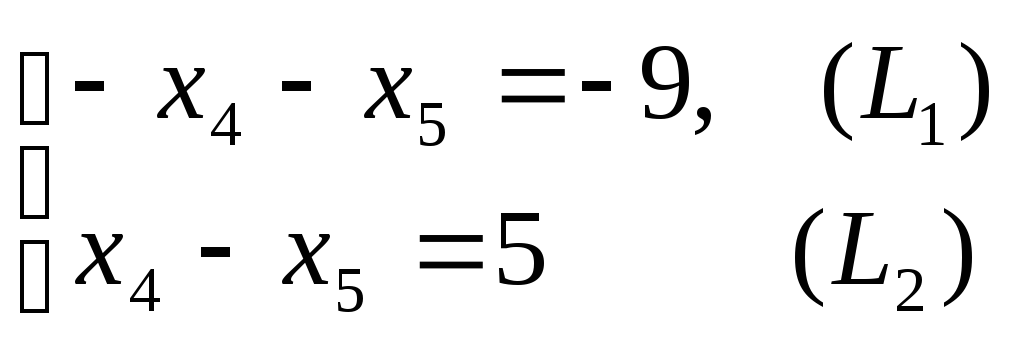
![]() .
Значит,
.
Значит,![]()
Вычисляем минимальное значение целевой функции
![]()
Находим оптимальное решение исходной задачи. Для этого используем систему ограничений в разрешенном виде:
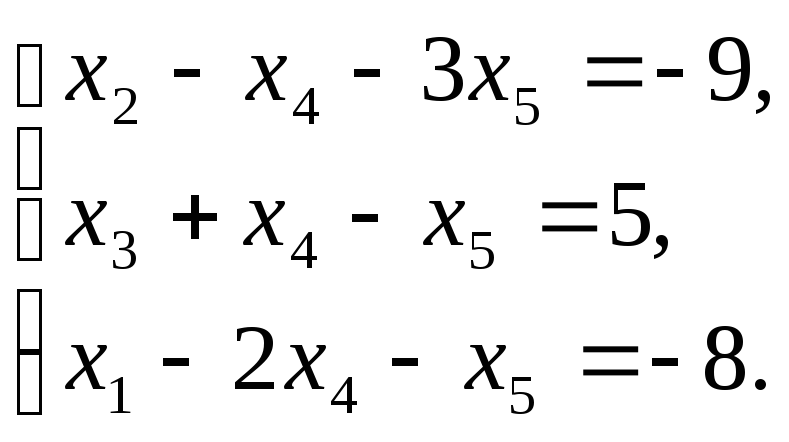
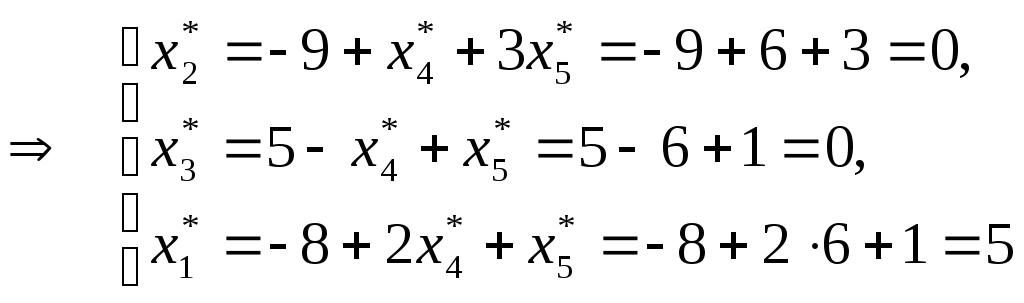
Получаем
![]()
Ответ:
![]()