Постановка задачи

Дана система нелинейных уравнений с неизвестными:

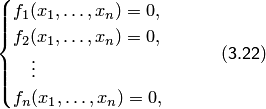
где , — нелинейные функции, определенные и непрерывные в некоторой области , или в векторном виде (где )

Требуется найти такой вектор , который при подстановке в систему (3.22) превращает каждое уравнение в верное числовое равенство.

Решить методом простых итераций.

для применения метода требуется привести систему (3.22) к равносильному виду:

(3.24)

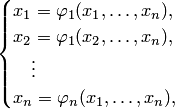
или в векторной форме

(3.25)

где , функцииопределены и непрерывны в окрестности изолированного решениясистемы (3.24).

17.)

Аппроксимацией (приближением) функции называется нахождение такой функции(аппроксимирующей функции), которая была бы близка заданной.

Функция f(x), в зависимости от специфики задачи, может отвечать различным требованиям.

• Функция f(x) должна проходить через точки (x_i,y_i), т. е. f(x_i)=y_i,i=1...n. В этом случае говорят обинтерполяцииданных функцией f(x) во внутренних точках между x_i, или экстраполяции за пределами интервала, содержащего все x_i.

• Функция f(x) должна некоторым образом (например, в виде определенной аналитической зависимости) приближать y(x_i), не обязательно проходя через точки (x_i,y_i). Такова постановка задачирегрессии, которую во многих случаях также можно назвать сглаживанием данных.

• Функция f(x) должна приближать экспериментальную зависимость y(x_i), учитывая, к тому же, что данные (x_i,y_i) получены с некоторой погрешностью, выражающей шумовую компоненту измерений. При этом функция f(x), с помощью того или иного алгоритма уменьшает погрешность, присутствующую в данных (x_i,y_i). Такого типа задачи называют задачами фильтрации. Сглаживание - частный случай фильтрации.

Критерии близости функций имогут быть различные.

В том случае, когда приближение строится на дискретном наборе точек, аппроксимацию называют точечной или дискретной.

В том случае, когда аппроксимация проводится на непрерывном множестве точек (отрезке), аппроксимация называется непрерывной или интегральной. Примером такой аппроксимации может служить разложение функции в ряд Тейлора, то есть замена некоторой функции степенным многочленом.

Типичной задачей аппроксимации функций является задача интерполяции. Необходимость интерполяции функций в основном связана с двумя причинами:

1. Функция f(x) имеет сложное аналитическое описание, вызывающее определенные трудности при его использовании (например, f(x) является спецфункцией: гамма-функцией, эллиптической функцией и др.).

2. Аналитическое описание функции f(x) неизвестно, т. е. f(x) задана таблично. При этом необходимо иметь аналитическое описание, приближенно представляющее f(x) (например, для вычисления значений f(x) в произвольных точках, определения интегралов и производных от f(x) и т. п.)

Постановка задачи интерполяции

 

На отрезке [a, b] заданы n + 1 точки x_i = х₀, х₁, . . ., х_n, которые называются узлами интерполяции, и значения некоторой функции f(x)  в этих точках

f(x0) = y0, f(x1) =  y1,  . . ., f(xn) = yn.

(1)

Требуется построить функцию F (х) (интерполяционная функция), принадлежащую известному классу и принимающую в узлах интерполяции те же значения, что и f(x), т. е. такую, что

F(x0) = y0, F(x1) =  y1,  . . ., F(xn) = yn.

(2)

Геометрически это означает, что нужно найти кривую y = F (х) некоторого определенного типа, проходящую через заданную систему точек M(x_i, y_i) (i = 0, 1, ..., n).

 

 

В такой общей постановке задача может иметь бесконечное множество решений или совсем не иметь решений.

Однако эта задача становится однозначной, если вместо произвольной функции F (х) искать полином j (х) (интерполяционный полином) степени не выше n, удовлетворяющий условиям (2), т. е. такой, что

j (x0) = y0, j (x1) =  y1,  . . ., j (xn) = yn.

(3)

Полученную интерполяционную формулу

(4)

обычно используют для приближенного вычисления значений данной функции ¦ (х) для значений аргумента х, отличных от узлов интерполяции. Такая операция называется интерполяцией функций.

Различают два вида интерполяции:

1. глобальная - соединение всех точек ¦ (х) единым интерполяционным полиномом;

2. локальная - соединение точек отрезками прямой (по двум точкам), отрезками параболы (по трем точкам).

18.)

Интерполяционным полиномом называется соответствующий интерполянт, в котором в качестве системы функций φ_k(x), выбирается полином.

Существование и единственность интерполяционного полинома гарантируется, если все узлы интерполяции x_k различны. Т.к определитель системы линейных алгебраических уравнений для нахождения коэффициентов a_k является определителем Вандермонда, который, равен

и, следовательно, отличен от нуля в случае, когда все узлы x_k различны и матрица системы невырождена, то решение системы существует и единственно.