Математическим моделированием¹называется изучение реального объекта на ЭВМ с помощью математической модели этого объекта.

Математическая модель – это приближенное математическое описание объекта (технологического процесса, реакции, явления и т.д.).

Примеры простейших моделей:

-уравнение состояния идеального газа

F =-закон всемирного тяготения

-закон сохранения энергии

-закон Кулона

-закон сохранения энергии для фотона, где v – частота излучения.

Основные этапы математического моделирования:

1. Разработка модели – формализация. Изучается в прикладных и фундаментальных науках.

2. Разработка метода (алгоритма) решения уравнения модели – алгоритмизация. Изучается в вычислительной математике.

3. Создание программы – программирование. Изучается в информатике.

4. Расчеты, анализ результатов – практическое использование.

Предметом вычислительной математики являются численные методы (алгоритмы) решения математических задач, возникающих при исследовании реальных объектов методом математического моделирования.

Вычислять новые приближения решения x_i по формуле:

x_i = - формула итерационного процесса

до достижения условия:

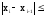- условие завершения итерационного процесса.

i = 1,2,.. – номер вычисления - итерации.

 – требуемая точность.

Число итераций влияет на точность решения. Решение, полученное итерационным методом, всегда является приближенным, так как точное решение получить невозможно – нужны бесконечные вычисления.

Виды численных методов:

1. Прямые – решение получают за конечное число арифметических действий.

2. Итерационные – точное решение может быть получено теоретически в виде предела бесконечной сходящейся последовательности вычислений.

3. Вероятностные – методы случайного поиска решения (угадывания).

2.) Точность решения задачи оценивается абсолютной или относительной погрешностью.

Абсолютная погрешность:

, где - точное решение,

x - численное решение.

Относительная погрешность:

,

Источники погрешности численного решения задачи:

1. Погрешность математической модели.

Возникает в результате допущений, принятых при получении модели. Реальность всегда сложнее любой модели, поэтому этот источник погрешности всегда влияет на численное решение. Величина этой погрешности определяется сравнением экспериментальных данных с результатами расчетов по модели (оценивается адекватность модели объекту).

2. Погрешность исходных данных. Зависит от точности измерения параметров, используемых в модели. Любые измерения приближенны, поэтому и этот источник всегда влияет на решение.

В вычислительной математике эти два вида погрешности (погрешность математической модели и погрешность исходных данных) принято называть неустранимой погрешностью, т.к. она не зависит от метода решения задачи и всегда влияет на ее решение, и ее обязательно нужно учитывать при анализе полученного решения.

3. Погрешность метода решения задачи. Возникает в результате применения итерационного или вероятностного метода решения. Эти методы позволяют получить точное решение только в результате бесконечной последовательности действий. Поэтому для получения приближенного решения бесконечный процесс прерывают при достижении требуемой точности решения.

4. Погрешность округления. Возникает в результате проведения вычислений с конечным числом значащих цифр.

Учесть погрешность округления при большом количестве арифметических действий практически невозможно.

Есть случайные и систематические источники погрешности округления.

Случайные источники обычно компенсируют друг друга.

Например:

Знаки случайны и компенсируют друг друга при большом n.

Систематические источники вызывают накопление погрешности округления. Они являются дефектом структуры вычислений (алгоритма).

В машинной арифметике законы коммутативности (переместительный) и дистрибутивности (распределительный) не всегда соблюдаются.

_{Рекомендации для снижения ошибок округления:}

1. _{При сложении и вычитании последовательности чисел действия необходимо начинать с наименьших по абсолютной величине значений.}

2. _{Следует избегать вычитания двух близких чисел, преобразуя выражения.}

3. _{Количество арифметических действий для решения задачи нужно сводить к минимуму.}

4. _{Для уменьшения ошибки округления расчеты следует проводить с повышенной разрядностью (double precision в Pascal).}

_{При выборе численного метода решения задачи необходимо учитывать следующее:}

1. _{Погрешность метода должна быть на порядок меньше неустранимой погрешности. Увеличение погрешности метода снижает точность, уменьшение – увеличивает время решения задачи.}

2. _{Погрешность округления должна быть значительно меньше (на два порядка) погрешности метода и неустранимой погрешности.}

_{Для оценки погрешности решения на практике можно использовать следующие приемы:}

1. _{Решить задачу различными численными методами и результаты сравнить.}

2. _{Незначительно изменить исходные данные и повторно решить задачу. Результаты сравнить. Если они различаются сильно, задача или метод ее решения являются неустойчивым – выбрать другой.}

3.) Пусть в результате решения задачи по исходному значению величины x  находится значение искомой величины y. Если исходная величина имеет абсолютную погрешность  x, то решение имеет погрешность y. Задача называется устойчивой по исходному параметру x, если решение y непрерывно от него зависит, т. е. малое приращение исходной величины x  приводит к малому приращению искомой величины y. (малые погрешности в исходной величине приводят к малым погрешностям в результате расчетов.) Отсутствие устойчивости означает, что даже незначительные погрешности в исходных данных приводят к большим погрешностям в решении или к неверному результату.

Задача называется поставленной корректно, если для любых значений исходных данных из некоторого класса ее решение существует, единственно и устойчиво по исходным данным. 

Численный алгоритм (метод) называется корректным в случае существования и единственности численного решения при любых значениях исходных данных, а также в случае устойчивости этого решения относительно погрешностей исходных данных. 

 Сходимость численного метода-  близость получаемого численного решения задачи к истинному решению.

Сходимость итерационного процесса- этот процесс состоит в том, что для решения некоторой задачи и нахождения искомого значения определяемого параметра (например, корня нелинейного уравнения) строится метод последовательных приближений. В результате многократного повторения этого процесса (или итераций) получаем последовательность значений x₁, x₂,…, x_n,… Говорят, что эта последовательность сходится к точному решению x = a, если при неограниченном возрастании числа итераций предел этой

последовательности существует и равен a:-  сходящийся численный метод. 

4.)

Всякое значение , удовлетворяющее условию, называетсякорнем уравнения , а способ нахождения этого значения и естьрешение уравнения.

Методы решения уравнений:

• Прямые (формула Виета для квадратного уравнения и Кардано для кубического и другие)

• Итерационные – для решения любого уравнения

 Общая постановка задачи: Найти действительные корни уравнения , где - алгебраическая или трансцендентная функция.

Численное решение уравнения проводится в два этапа:

1 этап. Отделение корней уравнения.

2 этап. Уточнение интересующих корней с заданной точностью ε.

Отделение корней – это определение их наличия, количества и нахождение для каждого из них достаточно малого отрезка [a,b], которому он принадлежит.

На первом этапе определяется число корней, их тип. Определяется интервал, в котором находятся эти корни, или определяются приближенные значения корней.

Задача отделения вещественных корней решается аналитическими и графическими методами.

Аналитические методы основаны на функциональном анализе.

Для алгебраического многочлена n-ой степени (полинома) с действительными коэффициентами вида

P_n(x) = a_n x ⁿ + a_n-1x^n-1 +...+a₁x+ a₀ = 0, (a_n >0)

верхняя граница положительных действительных корней определяется по формуле Лагранжа (Маклорена):

,

где: k  1 – номер первого из отрицательных коэффициентов полинома;

B – максимальный по модулю отрицательный коэффициент.

Нижнюю границу положительных действительных корней можно определить из вспомогательного уравнения

Если для этого уравнения по формуле Лагранжа верхняя граница равна R₁, то

=

Тогда все положительные корни многочлена лежат в интервале

≤x⁺≤.

Интервал отрицательных действительных корней многочлена определяется с использованием следующих вспомогательных функций.

и .

≤x^–≤= =.

Постановка задачи:

Отделить корни уравнения, используя аналитический метод:

Методом Лагранжа определим границы положительных и отрицательных корней многочлена.

3x⁸ – 5x⁷ – 6x³ – x – 9 = 0

k = 1 B = |– 9| a_n = 3

= 4

9x⁸ + x⁷ + 6x⁵ + 5x – 3 = 0

k = 8 B = 3 a_n = 9

Отсюда границы положительных корней 0,5 ≤ x⁺ ≤ 4

3x⁸ + 5x⁷ + 6x³ + x – 9 = 0

=

9x⁸ – x⁷ – 6x⁵ – 5x – 3 = 0

k = 1 B = 6 a_n = 9

Следовательно, границы отрицательных корней –2 ≤ x^– ≤ –0,6

Формула Лагранжа позволяет оценить интервал, в котором находятся все действительные корни, положительные или отрицательные. Поэтому, для определения расположения каждого корня необходимо проводить дополнительные исследования.

Для трансцендентных уравнений не существует общего метода оценки интервала, в котором находятся корни. Для этих уравнений оцениваются значения функции в особых точках: разрыва, экстремума, перегиба и других.

Графически корни можно отделить 2-мя способами:

1. Построить график функции y = f(x) и определить координаты пересечений с осью абсцисс− это приближенные значения корней уравнения.

y=f(x)

x

y

x₁^*

a

b x₂^* x₃^*

На графике 3 корня.

Первый корень

x^*  [a,b]

Отделение корней на графике f(x).

y=f(x)

2. Преобразовать f(x)=0 к виду (x) = (x), где (x) и (x) – элементарные функции, и определить абсциссу пересечений графиков этих функций.

На графике 2 корня.

Первый корень

x₁^*  [a,b]

Отделение корней по графикам функций (x) и (x).

Схема алгоритма отделения корней.

5.)

Уточнение корня – это вычисление интересующего корня с заданной точностью .

Приближённые значения корней уравнения, полученные на предыдущем этапе, уточняются различными итерационными методами.

Метод дихотомии (половинного деления, бисекций)- (дихотомия - сопоставленность или противопоставленность двух частей целого) при нахождении корня уравнения f(x)=0 состоит в делении пополам отрезка [a; b], где находится корень.

Алгоритм метода.

1. Вычислить координату середины отрезка [a,b] x = (a+b)/2 и значение (x в этой точке.

2. Уменьшить отрезок, отбросив ту его половину, на которой корня нет.

Если знак функции в начале отрезка и в его середине одинаков, то корень находится на второй половине, первую половину можно отбросить, переместив начало отрезка в его середину:

если (a ·(x>0 => x^* [x,b] => a=x, иначе x^* [a, x] => b=x

3. Проверить условие завершения вычислений : длина отрезка не превышает заданную точность и значение функции близко к 0 с заданной точностью:

b-a ≤ ε ∩ |(x| ≤ ε.

Если условие достигнуто, расчет завершен, иначе повторить алгоритм сначала.

Геометрическая интерпретация.

Bisection

Входные данные:

 – заданная точность;

a – левая граница отрезка;

b – правая граница отрезка.

1

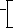
y_a =f(a)

y_b =f(b)

2

y_ay_b0

нет

3

да

4

i=0

11

Вывод

"Корней нет"

5

i = i+1;

x =(a+b)/2

12

Stop

y=f(x)

6

нет

y_ay>0

7

да

b=x

a=x

8

7

|y|/\ b-a<ε

нет

9

да

10

Выходные данные:

x – приближенное значение корня;

y – значение функции при найденном корне х;

i – выполненное число итераций.

Exit

Схема алгоритма метода бисекций (дихотомии)

6.) Метод Ньютона (касательных)- основан на стратегии постепенного уточнения корня.

Геометрическая интерпретация метода Ньютона.

Уточнение корня – это вычисление интересующего корня с заданной точностью .

Приближённые значения корней уравнения, полученные на предыдущем этапе, уточняются различными итерационными методами.

На отрезке существования корня выбирается начальное приближение x₀. К кривой f(x) в точке А с координатами (x₀, f(x₀)) проводится касательная. Абсцисса x₁ точки пересечения этой касательной с осью ОХ является новым приближением корня.

Из рисунка следует, что x₁ = x₀ − CB

Из ∆ABC: CD=. Но.

Следовательно,

Аналогично, для i-го приближения можно записать формулу итерационного процесса метода Ньютона:

, где x₀  [a;b]. (3.13)

Условие окончания расчета: 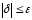, (3.14)

где −корректирующее приращение или поправка.

Условие сходимости итерационного процесса:

(3.15)

Если на отрезке существования корня знаки ине изменяются, то начальное приближение, обеспечивающее сходимость, нужно выбрать из условия

, x₀[a;b]. (3.16)

т.е. в точке начального приближения знаки функций и ее второй производной должны совпадать.

Геометрическая иллюстрация выбора начального приближения: график f(x) вогнутый, 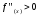, тогдаx₀=b, т.к. f(b)>0.

Если же выбрать x₀=a, то итерационный процесс будет сходиться медленнее или даже расходиться (см. касательную для x₀=a).

Геометрическая иллюстрация выбора начального приближения: график

f(x) выпуклый, f ’’(x)<0 , тогда x₀ =a, т.к. f(a)<0.

Схема алгоритма метода Ньютона:

7.) Метод хорд (секущих).

Этот метод применяется при решении уравнений вида , если корень уравнения отделён, т.е.  и выполняются условия:

1) (функция  принимает значения разных знаков на концах отрезка );

2) производная  сохраняет знак на отрезке  (функция  либо возрастает, либо убывает на отрезке ).

Первое приближение корня находится по формуле: .

Для следующего приближения из отрезков  и  выбирается тот, на концах которого функция  имеет значения разных знаков.

Тогда второе приближение вычисляется по формуле:

, если  или , если .

Вычисления продолжаются до тех пор, пока не перестанут изменяться те десятичные знаки, которые нужно оставить в ответе.

Геометрическая интерпретация нахождение решения методом хорд:

При решении уравнения методом хорд поводится прямая соединяющая концы отрезка [a,b]. Из двух точек А и В выбирается х0. Находится точка пересечения хорды с осью OX. Определяется значение функции в точке пересечения и из найденной точки проводится новая хорда. Этот процесс повторяется до получения необходимой точности.

Формула для n-го приближения имеет вид(х0=а , xn-1=b,xn=x):

В методе хорд условием окончания итераций является:

- условие близости двух последовательных приближений : ;

- условие малости невязки (величина F(xn) есть невязка, полученная на n-й итерации, а -число , с заданной точностью которого необходимо найти решение).

Описание алгоритма метода хорд  Шаг 1. Ввод a,b,ε.  Шаг 2. X:=a-f(a)×(b-a)/(f(b)-f(a)).  Шаг 3. Если dF2(b)×F(b)<0, то a:=x;  Если dF2(a)×F(a)<0, то b:=x;  Шаг 4. Пересчитать X по формуле шага 2.  Шаг 5. Выполнять шаг 3, пока abs(b-a)<=eps.  Шаг 4.Вывод результата – x.  Опишем назначение переменных и функций, используемых в процедуре Hord  dF2 – значение второй производной в точке Х  F – значение функции в точке Х  Х0 – начальное значение Х  А – левая граница  В – правая граница  Е – точность вычислений  Fa – значение функции в точке А  Fb - значение функции в точке В  Представим в виде структурной схемы.

 Блок схема алгоритма метода хорд:

1. 8.) Метод простых итераций (метод последовательных приближений)- метод реализует стратегию постепенного уточнения значения корня.

x_i=φ(x_i-1) , i=1,2,… где i − номер итерации.- последовательное вычисление значений x_i по формуле называется итерационным процессом метода простых итераций, а сама формула - формулой итерационного процесса метода.

Алгоритм решения нелинейного уравнения методом простых итераций:

Если , то итерационный процесссходящийся .

Условие сходимости

Точное решение x^* получить невозможно, так как требуется бесконечный итерационный процесс.

Можно получить приближенное решение, прервав итерационный x_i=φ(x_i-1) при достижении условия

,

где ε - заданная точность; i - номер последней итерации.

В большинстве случаев условие завершения итерационного процесса обеспечивает близость значения x_i к точному решению:

Геометрическая иллюстрация метода простых итераций:

1) Итерационный процесс для случая 0<<1x[a,b].:

2) Итерационный процесс для случая -1<<1x[a,b].:

3)Итерационный процесс для случая >1x[a,b].

4)Итерационный процесс для случая  - 1 x[a,b].