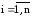Алгоритм метода Зейделя

1. Преобразовать систему к виду одним из описанных способов.

2. Задать начальное приближение решения произвольно или положить , а также малое положительное число (точность). Положить .

3. Произвести расчеты по формуле (1)или (2) и найти .

(2)

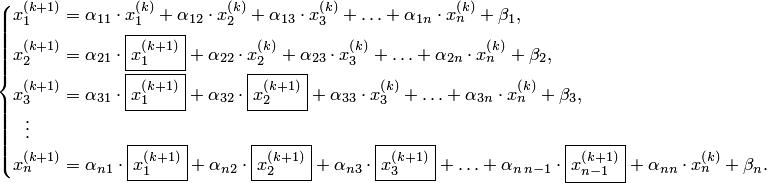(1)

4. Если выполнено условие окончания , процесс завершить и в качестве приближенного решения задачи принять . Иначе положить и перейти к пункту 3.

15.)

Решение систем нелинейных уравнений (СНУ).

Запишем систему n нелинейных уравнений с n неизвестными (СНУ) в общем виде:

f₁(x₁, x₂, …, x_n) = 0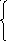

f₂(x₁, x₂, …, x_n) = 0 (5.1)

…

f_n(x₁, x₂, …, x_n) = 0

Эту систему можно записать в компактной, операторной форме:

F(X) = 0 (5.2)

где

вектор-функция

вектор неизвестных

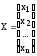
Решением системы называется набор значений 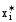,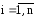(векторX^*), при которых все функции f_i равны 0 (система (5.1) обращается в тождество.)

СНУ могут иметь единственное решение, множество решений или вообще не иметь его. Поэтому численное решение СНУ проводят в два этапа:

1 этап – отделение решений.

2 этап – уточнение всех или только нужных решений.

Отделить решения – значит установить количество решений, определить приближенные значения каждого из них или указать область, в которой решение существует и является единственным.

Задача отделения решений достаточно просто решается только для системы двух уравнений с двумя неизвестными.

f₁(x₁, x₂) = 0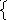

f₂(x₁, x₂) = 0

Для этого необходимо в координатах (x₁, x₂) построить кривые

f₁(x₁,х₂) = 0, f₂(x₁,х₂) = 0.

Точки пересечения этих кривых являются решениями системы. Так как координаты точек пересечения определяются приближенно, целесообразно говорить об области существования решения D. Эта область задается интервалами по каждой координате, внутри которых находятся искомые значения неизвестных.

Имеется два решения.

D₁ – область существования первого решения.

D₁ = {a₁ < x ₁< b₁ , a₂ < x ₂< b₂}.

Графическое отделение решений СНУ.

Для систем с большим числом неизвестных (n  3) удовлетворительных общих методов определения области существования решения нет. Поэтому при решении СНУ эта область обычно определяется при анализе решаемой задачи, например, исходя из физического смысла неизвестных.

Отделение решений позволяет:

1. Выявить число решений и область существования каждого из них.

2. Проанализировать возможность применения выбранного метода решения СНУ в каждой области.

3. Выбрать начальное приближение решения X⁽⁰⁾ из области его существования, так что X⁽⁰⁾D.

При отсутствии информации об области существования решения СНУ выбор начального приближения X⁽⁰⁾ проводиться методом проб и ошибок (методом “тыка”).

Постановка задачи.

Требуется решить систему нелинейных уравнений  . В координатном виде эту задачу можно записать так: , где 1 ≤ k ≤ n.

Убедиться в существовании решения и количестве корней, а также выбрать нулевое приближение в случае системы двух уравнений с двумя неизвестными можно, построив графики функций в удобных координатах. В случае сложных функций можно посмотреть поведение аппроксимирующих их полиномов. Для трех и более неизвестных, а также для комплексных корней, удовлетворительных способов подбора начального приближения нет.

16.)

Метод простых итераций.

Как и в случае одного уравнения, метод простых итераций заключается в замене исходной системы уравнений

f₁(x₁, x₂, …, x_n) = 0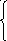

f₂(x₁, x₂, …, x_n) = 0

…

f_n(x₁, x₂, …, x_n) = 0 (5.1)

эквивалентной системой X=Φ(X) –(5.3) и построении итерационной последовательности

(5.4)-X^(k) = Φ(X^(k-1)) , где k=1,2,3,… - номер итерации,которая при k→∞ сходится к точному решению.

Здесь - итерирующая вектор-функция, X⁽⁰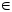⁾ D – начальное приближение решения.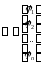

В развернутом виде формула итерационного процесса (выражение для вычисления очередного k-го приближения решения) имеет вид:

x_i.^(k) = φ_i(x₁^(k-1), x₂^(k-1), … , x_n^(k-1)), .(5.5)

Условие окончания расчета

δ≤ε (5.6)

где ε  заданная точность решения;

δ = 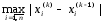(5.7)

или

δ = 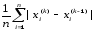(5.8)

Итерационный процесс (5.5) сходиться к точному решению, если в окрестности решения соблюдаются условия сходимости:

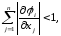
(5.9)

или

(5.10)

Таким образом, для уточнения решения СНУ методом простых итераций нужно найти такое эквивалентное преобразование (5.1) в (5.3), чтобы в области существования решения выполнялись условия (5.9) или (5.10).

В простейшем случае эквивалентную систему можно получать как:

,

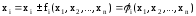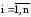
Можно выделить (не обязательно явно) все неизвестные из уравнений системы так, что:

,

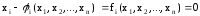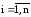
Как и в случае одного уравнения задачу поиска эквивалентного преобразования можно свести к задаче определения (в простейшем случае подбора) значений констант _i ≠ 0, 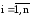, обеспечивающих сходимость

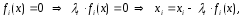
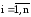
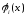
Схема алгоритма метода простых итераций.

Сходимость метода простых итераций можно несколько улучшить, если при вычислении очередного приближения 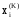использовать уже найденные значения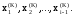

Рисунок 5.1. Схема алгоритма метода простых итераций

Выражение для расчета очередного к-го приближения примет вид:

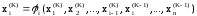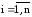, ; (5.11)

Для реализации данного приема, аналогичного методу Гаусса-Зейделя для систем линейных уравнений, в алгоритм расчета следует внести изменения: формулу расчета очередного приближения (символ 5) записать как X=φ(x) или в развернутом виде:

,

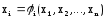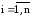
Существуют и другие приемы улучшения сходимости метода простых итераций. Например, новое приближение вычислять как среднее арифметическое двух предшествующих приближений:

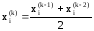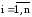, (5.12)

Можно использовать поправку Эйткена для улучшения сходимости:

,
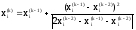