Тема 7. Различные виды резонаторов.

1.Резонаторы в виде отрезков регулярных линий передачи.

Р

Рис.40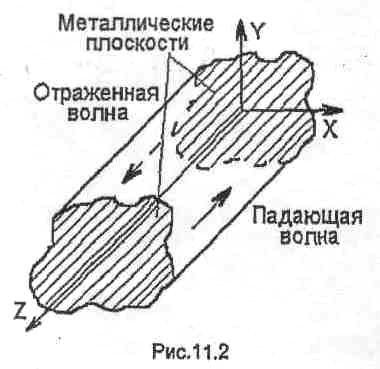

ассмотрим, например, отрезок закрытой линии передачи, в котором возбуждена волна одного типа, распространяющаяся в направлении, указанном на рис.40 сплошной стрелкой. Конец линии, удаленный от точки питания, замкнем накоротко с помощью идеально проводящей металлической пластины, перпендикулярной продольной оси линии (режим короткого замыкания). Начало координат совместим с короткозамыкающей плоскостью, ориентировав ось z параллельно продольной оси линии . Так как коэффициент отражения от идеально проводящей плоскости для касательной к ней (т.е. перпендикулярной оси. Z) составляющей вектора напряженности электрического поля равен -1, то комплексная амплитуда этой составляющей в произвольном сечении рассматриваемого отрезка определяется выражением, где-вектор, связанный с комплексной амплитудой напряженности электрического поля падающей волнысоотношением. Очевидно, что векторзависит только от поперечных (по отношению к оси Z) координат. Граничное условиеудовлетворяется одним типом волны.

Следовательно, при отражении от металлической плоскости, перпендикулярной оси Z, возбуждения более высоких по порядку либо более низких типов волн не происходит.

На рис.40 построена зависимость поперечной составляющей вектора Е от координаты z. На расстоянии от точки z = 0, где-длина волны в линии, а р- произвольное натуральное число. Поэтому, не нарушая структуры поля в направляющей системе, в любое из сечений, где поперечная составляющая напряженности электрического поля равна нулю, можно ввести еще одну короткозамыкающую металлическую плоскость, перпендикулярную оси Z. Но отрезок линии между двумя короткозамыкающими пластинами представляет собой объемокруженный со всех сторон металлической оболочкой, т.е. является объемным резонатором закрытого типа. Если направляющая система открытого типа, то короткозамкнутый с двух сторон отрезок линии является открытым резонатором.

Таким образом, длина объемного резонатора равна целому числу полуволн колебания, распространяющегося в линии:

(22)

Найдем резонансную длину волны резонатора:

(23)

Рис.41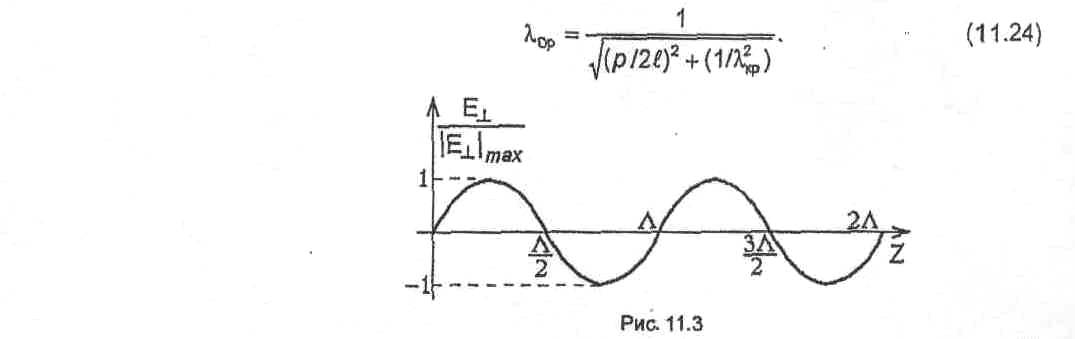

Классификация колебаний в объемных резонаторах, представляющих собой короткозамкнутый отрезок направляющей системы, осуществляется в соответствии с типом волны, стоячая волна которого образуется в резонаторе. Чтобы различать колебания с различным числом полуволн, укладывающихся вдоль оси Z резонатора, в указатель типа волны вводят дополнительный индекс р , равный числу полуволн в стоячей волне. Например, если в прямоугольном резонаторе колебание представляет собой стоячую волну, образованную в результате полного отражения волны, причем вдоль оси Z уложилось четыре полуволны, то такая структура поля обозначается.Аналогичный смысл имеют обозначения,,,.

Так как у ТЕМ-волн критическая длина волны равна бесконечности, то в случае колебанийвыражение (23) упрощается и принимает вид

(24)

Вывод формул (22) и (24) основан на предположении, что у волны, распространяющейся в линии передачи, обязательно существуют поперечные составляющие электрического поля, обращающиеся в нуль на короткозамыкающих пластинах. Для волни ТЕМ это условие, очевидно, выполняется всегда, так как у этих волн вектор электрического поля лежит в плоскости, перпендикулярной направлению распространения волны. У волн Е, как следует из выражений (9.14) и (9.19), припоперечные составляющие вектора напряженности электрического поля равны нулю в любом сечении линии передачи. В то же время продольная составляющая напряженности электрического поля и поперечный вектор магнитного поля отличны от нуля. Поэтому прикороткозамыкающие пластины можно вводить в произвольные сечения линии с волной, т.е. резонансная частота такого резонатора не зависит от его длины. Можно заметить, что данный результат есть частный случай (24), так какпри р = 0. Следовательно, у колебаний, тогда как у волн,всегда.

Рис.42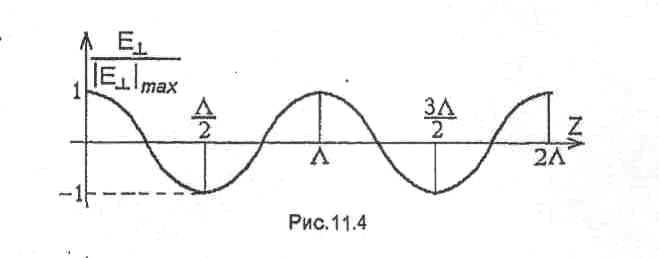

Зависимость поперечной составляющей вектора Е от координаты z показана на рис.42. Образуя второй обрыв рассматриваемой линии на расстоянии , p=1,2,.... от ее конца, получаем объемный резонатор.