5.3. Выбор и расчет элементов схемы усилителя с нагрузкой в цепи катода

Величина емкости конденсатора выбирается из условия допустимого искажения импульса. Расчет её может быть произведен по формуле:

(5.3.1)

где - внутреннее сопротивление промежутка лампы катод - вторая сетка;

- допустимое искажение импульса, спад плоской части вершины импульса;

- длительность импульса.

Конденсатор на допустимое напряжение выбирается по величине потенциала источника питания Но поскольку он подключен к катоду усилителя и находится под потенциалом выходного импульсного напряжения, то должен быть изолирован от корпуса.

Выбор емкости конденсатора, а также условия его эксплуатации, аналогичны

Необходимо заметить, что мощности рассеяния на резисторах и нельзя рассчитывать по величине среднего тока соответствующей сетки лампы, так как ток не зависит от выходного напряжения, а определяется напряжением превышения:

.

Мощность рассеяния на резисторах и зависит от амплитуды выходного напряжения. Для -

, (5.3.2)

где Q - скважность,

T - период следования импульсов.

В случае работы с группой импульсов -

m - количество импульсов в группе.

Мощность рассеяния на резисторе -

, (5.3.4)

Сопротивление резистора , рассчитанное по допустимому спаду группы импульсов, должно быть порядка 5÷15 ком. При этом мощность рассеяния на нем согласно (5.3.4) составит несколько десятков ватт при амплитуде выходного напряжения до 10 и более киловольт.

Резистор можно заменить дросселем.

5.4. Усилитель с импульсным питанием второй сетки.

_______

Есм

Еип

Сg1_g1

Uвх

Uвых

Lдр

Rk

Рис.5.3.

Для уменьшения габаритов схемы усилителя источник постоянного питания второй сетки можно заменить импульсным (рис.5.3.) и таким образом исключить из схемы конденсатор и резистор

Для анализа работы схемы усилителя с импульсным питанием второй сетки воспользуемся аппроксимацией характеристики тока лампы, приятной выше,

, (5.4.1)

где - амплитуда импульсного напряжения на второй сетке.

Решение дифференциального уравнения (5.2.2) будет иметь вид:

(5.4.2)

Потенциал запирания лампы при условии , будет определяться выражением

(5.4.3)

т.е. уменьшится на величину, равную

(5.4.3a)

Подставив значение из (5.4.3) в (5.4.2), получим величину выходного напряжения:

(5.4.4)

Установившееся значение амплитуды напряжения на выходе определяется при :

(5.4.5)

Из сравнения формул (5.2.8) и (5.4.5) видно, что коэффициент усиления каскада с импульсным питанием второй сетки значительно выше, следовательно, аналогичные параметры выходного сигнала получаются при меньших энергетических затратах, т.е. можно уменьшить величину амплитуды импульсов на второй и первой сетках.

Для усилителей с импульсным питанием второй сетки разработан малогабаритный трёхобмоточный импульсный трансформатор, с рабочим потенциалом относительно корпуса и обмоток до 10кв и высокопотенциальный импульсный дроссель, с рабочим напряжением в импульсе до 10кв при передаче группы импульсов на базе до 100мксек.

Время нарастания амплитуды импульса выходного напряжения можно определить из выражения (5.4.4), произведя некоторые преобразования:

.(5.4.6)

Время переходного процесса определялось по формулам (5.2.11) и (5.4.6) в предположении, что на вход лампы подан сигнал в виде функции единичного скачка. Общий вид формул будет несколько отличаться, если входной сигнал представить функцией времени U(t). Для решения поставленной задачи можно рассмотреть функцию включения трапецеидальной формы.

В этом случае за время действия переднего фронта импульсов Э.Д.С. меняется по линейному закону, т.е.

(5.4.7)

А так как питание второй сетки импульсное, то оно также будет функцией времени. Следовательно,

(5.4.7a)

(5.4.7б)

В общем случае ≠.

Аппроксимируя характеристику тока лампы (5.4.1) с учетом (5.4.3) и (5.4.7а,б), дифференциальное уравнение после преобразований запишем:

. (5.4.8)

Полученное уравнение линейное, неоднородное, правая часть его является функцией времени. Общее решение запишется:

(5.4.9)

- постоянная интегрирования, определяется из начальных условий

(5.4.9a)

Подставим (5.4.9а) в (5.4.9):

(5.4.10)

При 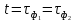выражение (5.4.10) запишется:

(5.4.11)

При второе слагаемое выражения (5.4.11) стремится к нулю и значение выражения (5.4.11) совпадает с (5.4.5), полученным при условии скачкообразного изменения входного сигнала.

При во втором слагаемом получаем неопределенность вида /. Для раскрытия этой неопределенности воспользуемся правилом Лопиталя.

Заменим отношение функций отношением их производных по и после несложных преобразований получим

(5.4.12)

Подставим полученное значение в (5.4.10) при

Таким образом, при граничных значениях времени, т.е. , выражение (5.4.11) совпадает с (5.4.4).

Формула (5.4.11) позволяет определить влияние изменения крутизны переднего фронта входного сигнала на длительность переднего фронта выходного сигнала при различных значениях емкости нагрузки.

Полагая, что скорости изменения сигналов на первой и второй сетках равны, представим эту формулу в следующем виде:

(5.4.13)

Очевидно, что выражение в фигурных скобках меньше либо равно 1 .Меняя длительность фронта входного сигнала , можем вычислить значение длительности переднего фронта выходного сигнала при различных значениях. Данные сведены в таблицу 5.4.1 и построены графики (рис.2.6) для лампы лучевого тетрода ГМИ-26Б с параметрами при импульсной мощности в нагрузке, равной 100квт.

Из таблицы 5.4.1 и графиков рис. видно, что длительность фронта на выходе равна

(5.4.14)

причем _фвых увеличивается не только от увеличения емкости в нагрузке, но и от уменьшения крутизны нарастания входного сигнала.

Величина ∆ определяет приращение длительности фронта выходного сигнала по отношению к входному.

Следовательно, изменение длительности переднего фронта выходного сигнала будем тем меньше, чем больше скорость изменения входного сигнала, т.е. чем меньше длительность фронта входного импульса.

Аналогичный выход сделан в работе при анализе процессов формирования фронта импульса в модуляторе с частичным разрядом емкости. Причиной возрастания длительности фронта импульса на нагрузке при уменьшении крутизны фронта сеточного напряжения объяснялось уменьшением зарядного тока конденсатора паразитной емкости

Очевидно, увеличение ∆ можно объяснить особенностью нелинейных преобразований импульсов и их спектральных функций.

Спектральная функция выходного сигнала -

аппроксимирующей характеристику нелинейного элемента.

Таблица 5.4.1

мксек
	0,01	0,05	0,1	0,15	0,01		0,05	0,1	0,15
1	2	3	4	5	6		7	8	9
0,01	0,10
0,015	0,18
0,02	0,7
0,025	0,96				0,294
0,03					0,701
0,0328					0,96
0,05		0,394	0,196	0,134			0,194	0,096	0,063
0,07		0,682
0,08		0,845
0,085		0,930
0,1			0,595	0,397			0,675	0,334	0,233
0,12			0,777				0,925	0,463
0,14			0,965
0,15				0,703				0,667	0,445
0,19				0,977				0,972	0,7
0,25									0,991

Форма воздействующего импульса тем меньше претерпевает изменения при нелинейном преобразовании, чем оно ближе к прямоугольной форме.

В пределе импульс строго прямоугольной формы, проходя через нелинейную цепь, не изменяет своей формы.