3.11. Косвенный метод чм модуляции

При косвенном методе генератор вырабатывает колебания стабильной частоты. Фаза этих колебаний варьируется приёмами фазового модулятора так, чтобы полезная девиация частоты была пропорциональна амплитуде модулирующего сигнала и не зависима от его частоты.

Для преобразования ФМ в ЧМ на входе фазового модулятора включается интегратор. Сигнал на выходе интегратора Uвых.(t) связан с входным сигналом Uвх.(t) соотношением:

Uвых(t)= .

При модулирующем сигнале Uмод(t) cosΩ t получим :

Uвых(t)= sinΩt

При этом для фазы сигнала имеем:

Δ(t) = KUвых(t) = sinΩt.

Для изменения мгновенной частоты сигнала при данной функции, получим:

Δω(t) = =sinΩt

Из этой формулы следует, что девиация частоты Δω_дев = =const, что и требуется иметь при ЧМ. При косвенном методе ЧМ небольшое значение девиации частоты Δω_дев,, которое можно получить, ограничивает область его использования. Повышение Δω_дев, возможно за счёт применения многоконтурных колебательных цепей или умножения частоты сигнала в n раз, т.е. девиация частоты увеличится в n раз и составит nΔω.

3.12. Фазовая модуляция.

Под фазовой модуляцией (ФМ) подразумевается изменение фазы колебания по закону передаваемой информации, т.е. изменения модулирующего напряжения. Эта задача может быть осуществлена различными способами. Наибольшее распространение получили узкополосные методы модуляции с дальнейшим увеличением индекса модуляции, основанные на преобразовании амплитудной модуляции в модуляцию фазы. Косвенный метод фазовой модуляции или прямой метод, основанный на изменении параметров цепи, к которой подводится высокочастотное колебание.

В фазовых модуляторах колебания от задающего генератора постоянной частоты проходят через устройство, которое изменяет их фазу по закону передаваемой информации. Поэтому задающий генератор может стабилизироваться кварцевым резонатором, что является основным преимуществом по сравнению с частотной модуляцией. Фаза колебаний, формируемая LC контуром, изменяется фазосдвигающими цепями различного вида. Управляемыми элементами могут быть реактивные и активные сопротивления. Основное требование к этим элементам – большое быстродействие, т.е. безынерционность управления. Наиболее применяемыми элементами – ёмкость p-n перехода диода или полевого транзистора.

Основной недостаток всех фазовых модуляторов – нелинейность модуляционной характеристики, вследствие чего невозможно получить высокий индекс фазовой модуляции, который можно значительно повысить умножением частоты.

3.12.1. Методы получения фазовой модуляции

Схема с балансным модулятором.

ЗГ

ФВ 90 ⁰

У

БМ

∑

Uвых

U _Ω

Колебания с ЗГ подаются один на вход БМ, второй на фа­зовращатель 90°. После фазовращателя колебания подаются на усилитель. Ко второму входу БМ подводится модулирующее напряжение U_Ω. С выхода БМ и У (усилителя) колебания поступают на каскад сумматора. Величина выходного напряжения зависит от глубины амплитудной модуляции и меняется от 0 до некоторого максимального значения. При U_Ω = 0, вектор U_вых не будет отклоняться, при U_Ω =U_Ωmax вектор U_вых будет отклоняться на наибольший угол. Величина этого угла и определяет фа­зовую модуляцию высокочастотных колебаний.

tg φ =,

Нелинейные искажения определяются по формуле:

К = ﴾U зг/U_Ω﴿² *m²

При m = 1 и Uзг = U_Ω величина φ_max = π/4 рад, а К = 8,3%. Дальнейшее увеличение фазы нецелесообразно.

Использование противофазной амплитудной модуляции представлено на структурной схеме (рис 3.19. ).

U1

ЗГ

ФВ 90⁰

АМ 1

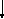
Uвых

∑

Сигнал U_Ω

АМ 2

U2

Рис. 3.19

Uвых получается от сложения векторов U₁ и U₂ . Когда U₁ растёт, U₂ падает и фаза выходного напряжения изменяется от 0 до 90⁰ . При U₁ = U₂ малые нелинейные искажения получаются при фазе не более 20 -30⁰ .