
- •Теория вероятностей
- •Содержание
- •Раздел 6. Законы распределения функций случайных аргументов. 90
- •1. Теоретическая часть. Введение
- •Раздел 1. Понятие события и его вероятности.
- •1.1. Предмет теории вероятности.
- •1.2. Алгебра событий. Пространство элементарных событий.
- •1.3. Классическое определение вероятности.
- •1.4. Геометрические вероятности.
- •1.5. Частота и вероятность.
- •1.6. Аксиоматическое построение теории вероятностей.
- •1.7. Условная вероятность и простейшие основные формулы.
- •1.8. Формула полной вероятности.
- •1.9 Формула Бейеса.
- •Раздел 2. Последовательные независимые испытания
- •2.1. Независимые испытания. Формулы Бернулли.
- •2.2. Обобщенная теорема о повторении опытов.
- •Раздел 3. Понятие случайной величины. Функция распределения и ее основные свойства.
- •3.1. Понятие случайной величины и функции распределения.
- •3.2. Свойства функции распределения.
- •3.3. Дискретные и непрерывные случайные величины.
- •3.4. Числовые характеристики случайных величин.
- •Раздел 4. Примеры распределений случайных величин.
- •4.1. Биномиальное распределение.
- •4.2. Теорема Пуассона
- •4.3. Закон Пуассона.
- •4.4. Равномерное распределение.
- •4.5. Показательное распределение.
- •4.6.Нормальный закон распределения.
- •Раздел 5. Системы случайных величин (случайные векторы).
- •5.1. Понятие о системе случайных величин.
- •5.2. Функция распределения системы двух случайных величин.
- •5.3. Плотность распределения системы двух случайных величин.
- •5.4. Законы распределения отдельных компонент, входящих в систему. Условные законы распределения.
- •5.5. Зависимые и независимые случайные величины.
- •5.6. Числовые характеристики системы двух случайных величин.
- •5.7. Система произвольного числа случайных величин (случайные вектора).
- •5.8. Числовые характеристики системы нескольких случайных величин.
- •Раздел 6. Законы распределения функций случайных аргументов.
- •6.1. Закон распределения функции одного случайного аргумента.
- •6.2. Закон распределения функции двух случайных величин.
- •6.3. Закон распределения суммы двух случайных величин. Композиция законов распределения.
- •6.4. Распределение произведения.
- •6.5. Распределение квадрата случайной величины.
- •6.6. Распределение частного.
- •6.7. Числовые характеристики функций случайных величин.
- •Раздел 7. Теоремы о числовых характеристиках.
- •7.1. Основные теоремы о математическом ожидании.
- •7.2. Теоремы о дисперсии случайной величины.
- •7.3. Теорема о линейной зависимости случайных величин.
- •Раздел 8. Характеристические функции.
- •8.1. Определение и простейшие свойства характеристических функций.
- •8.2. Предельные теоремы для характеристических функций.
- •Раздел 9. Предельные теоремы для случайных величин.
- •9.1. Сходимость последовательностей случайных величин.
- •9.2. Закон больших чисел.
- •9.3. Следствия закона больших чисел.
- •Раздел 10. Предельные теоремы теории вероятностей.
- •10.1. Центральная предельная теорема.
- •10.2. Теорема Ляпунова.
- •10.3. Теорема Лапласа.
- •2. Практические занятия, тесты, самостоятельная работа. Занятие 1. Непосредственный подсчет вероятности с использованием классического определения вероятности.
- •1.1. Краткая теоретическая часть.
- •1.2. Тест.
- •1.3. Решение типовых задач.
- •1.4. Задачи для самостоятельной работы.
- •Занятие 2. Геометрическое определение вероятности.
- •2.1. Краткая теоретическая часть.
- •2.2. Тест
- •2.3. Решение типовых задач
- •2.4. Задачи для самостоятельной работы
- •Занятие 3. Условная вероятность. Теорема умножения вероятностей.
- •3.1. Краткая теоретическая часть
- •3.2. Тест
- •3.3. Решение типовых задач
- •3.4. Задачи для самостоятельной работы
- •Занятие 4. Теорема сложения вероятностей.
- •4.1. Краткая теоретическая часть
- •4.2. Тест
- •4.3. Решение типовых задач
- •4.4. Задачи для самостоятельной работы
- •Занятие 5. Формула полной вероятности.
- •5.1. Краткая теоретическая часть
- •5.2. Тест.
- •5.3. Решение типовых задач
- •5.4. Задачи для самостоятельной работы
- •Занятие 6. Формула Бейеса.
- •6.1. Краткая теоретическая часть
- •6.2.Тест
- •6.3. Решение типовых задач
- •6.4. Задачи для самостоятельной работы
- •Занятие 7. Последовательные независимые испытания.
- •7.1. Краткая теоретическая часть
- •7.2. Тест
- •7.3. Решение типовых задач
- •7.4. Задачи для самостоятельной работы
- •Занятие 8. Дискретные и непрерывные случайные величины.
- •8.1. Краткая теоретическая часть а) Ряд, многоугольник и функция распределения случайной дискретной величины
- •8.2. Тест
- •А) только к дискретным случайным величинам
- •8.3. Решение типовых задач а) Ряд, многоугольник и функция распределения случайной дискретной величины
- •Б) Функция распределения и плотность вероятности непрерывной случайной величины
- •8.4. Задачи для самостоятельной работы а) Ряд, многоугольник и функция распределения случайной дискретной величины
- •Занятие 9. Числовые характеристики дискретных случайных величин.
- •9.1. Краткая теоретическая часть
- •9.2. Тест
- •9.3. Решение типовых задач
- •9.4. Задачи для самостоятельной работы
- •Занятие 10. Дискретные и непрерывные случайные величины.
- •10.1. Краткая теоретическая часть
- •10.2. Тест
- •10.3. Решение типовых задач
- •10.4. Задачи для самостоятельной работы
- •Занятие 11. Закон Пуассона.
- •11.1. Краткая теоретическая часть
- •11.2. Тест
- •11.3. Решение типовых задач
- •11.4. Задачи для самостоятельной работы
- •Занятие 12. Закон нормального распределения.
- •12.1. Краткая теоретическая часть
- •12.2. Тест
- •12.3. Решение типовых задач
- •12.4. Задачи для самостоятельной работы
- •Литература
Занятие 11. Закон Пуассона.
11.1. Краткая теоретическая часть
Законом распределения Пуассона называется ряд распределения случайной величины X вида
![]() ,
,
где
![]() .
.
Законом Пуассона может быть приближенно заменено биномиальное распределение, когда вероятность р появления события А в каждом отдельном опыте мала, а число п производимых опытов велико. В этом случае имеет место приближенное равенство
![]() ,
,
где
![]() .
.
11.2. Тест
Распределенными по закону Пуассона могут быть:
а) только дискретные случайные величины
б) только непрерывные случайные величины
в) и дискретные, и непрерывные случайные величины
Является ли обязательным условие, что случайная величина может быть распределенной по закону Пуассона только в случае, если она принимает целочисленные значения?
а) Да
б) Нет
Законом распределения Пуассона называется ряд распределения случайной величины
 вида
вида
а) ![]()
б) ![]()
в) ![]()
г) ![]()
д) ![]()
Математическое ожидание и дисперсия случайной величины, распределенной по закону Пуассона, обладают следующим свойством:
а) равны нулю
б) равны между собой
в) равны параметру Пуассона
11.3. Решение типовых задач
Пример 11.1. Радиоаппаратура состоит из 1000 электроэлементов. Вероятность отказа одного элемента в течение одного года работы равна 0,001 и не зависит от состояния других элементов. Какова вероятность отказа двух и не менее двух электроэлементов за год?
Решение.
Считая случайное число X отказавших элементов подчиняющимся закону Пуассона
![]() ,
где
,
где
![]() ,
получим:
,
получим:
1) вероятность отказа ровно двух элементов
![]() ;
;
2) вероятность отказа не менее двух элементов
![]() .
.
П ример
11.2.При
разрыве баллона в процессе испытания
на прочность образовалось 100 осколков,
распределившихся
равномерно в «конусе разлета», т. е. в
области, ограниченной
двумя коническими поверхностями с
углами 30°
и 60° (см. рис.). Найти математическое
ожидание и дисперсию
числа осколков, приходящихся на 1 м2
части
поверхности
сферы, находящейся внутри конуса разлета,
если радиус
сферы 50 м,
а
центр ее совпадает с точкой разрыва.
ример
11.2.При
разрыве баллона в процессе испытания
на прочность образовалось 100 осколков,
распределившихся
равномерно в «конусе разлета», т. е. в
области, ограниченной
двумя коническими поверхностями с
углами 30°
и 60° (см. рис.). Найти математическое
ожидание и дисперсию
числа осколков, приходящихся на 1 м2
части
поверхности
сферы, находящейся внутри конуса разлета,
если радиус
сферы 50 м,
а
центр ее совпадает с точкой разрыва.
Решение.
Пересечем конус разлета осколков сферой радиуса 50 м и определим математическое ожидание числа осколков, приходящихся на единицу площади поверхности шарового пояса, образовавшегося в результате пересечения конуса разлета со сферой. Обозначим через S площадь поверхности шарового пояса:
 м2
м2
Так как общее число осколков N=100, то математическое ожидание числа их а, приходящегося на единицу площади поверхности шарового пояса, будет
![]() осколка.
осколка.
Вероятность
попадания данного осколка в данную
площадку
![]() м2
мала
(она
равна
м2
мала
(она
равна
![]() ,
а направления
полета осколков взаимно независимы;
поэтому
можно считать, что случайное число
осколков X,
приходящееся
на 1 м2
поверхности
сферы, распределено по закону Пуассона
и, следовательно, имеет место равенство
,
а направления
полета осколков взаимно независимы;
поэтому
можно считать, что случайное число
осколков X,
приходящееся
на 1 м2
поверхности
сферы, распределено по закону Пуассона
и, следовательно, имеет место равенство
![]() .
.
11.4. Задачи для самостоятельной работы
11.1. Математическое ожидание числа отказов радиоаппаратуры за 10000 часов работы равно 10. Определить вероятность отказа радиоаппаратуры за 100 часов работы.
(Ответ:
![]() )
)
11.2. Вероятность того, что любой абонент позвонит на коммутатор в течение часа равна 0,01. Телефонная станция обслуживает 300 абонентов. Какова вероятность, что в течение часа позвонят 4 абонента?
(Ответ:
![]() )
)
11.3. Аппаратура содержит 2000 одинаково надежных элементов, вероятность отказа для каждого из которых равна р = 0,0005. Какова вероятность отказа аппаратуры, если он наступает при отказе хотя бы одного из элементов?
(Ответ:
![]() )
)
11.4. В течение часа коммутатор получает в среднем 60 вызовов. Какова вероятность того, что за время 30 сек, в течение которых телефонистка отлучилась, не будет ни одного вызова?
(Ответ:
![]() )
)
11.5. Вероятность того, что изделие не выдержит испытания, равна 0,001. Найти вероятность того, что из 5000 изделий более чем одно не выдержит испытания. Сравнить результаты расчетов, полученных с использованием распределения Пуассона и с использованием биномиального распределения. В последнем случае расчет производить с помощью семизначных таблиц логарифмов.
(Ответ: 1) 0,95958; 2) 0,95963)
11.6. За рассматриваемый период времени среднее число ошибочных соединений, приходящееся на одного телефонного абонента, равно 8. Какова вероятность, что для данного абонента число ошибочных соединений будет больше 4?
(Ответ: 0,9)
11.7. Найти вероятность того, что среди 200 изделий окажется более трех бракованных, если в среднем бракованные изделия составляют 1%.
(Ответ: 0,143)
11.8. Корректура в 500 страниц содержит 500 опечаток. Найти вероятность того, что на странице не меньше трех опечаток.
(Ответ:
![]() )
)
11.9.
В
наблюдениях Резерфорда и Гейгера
радиоактивное
вещество за промежуток времени 7,5 сек,
испускало в
среднем 3,87
![]() -частицы.
Найти вероятность того, что за 1 сек это
вещество испустит хотя бы одну
-частицы.
Найти вероятность того, что за 1 сек это
вещество испустит хотя бы одну![]() -частицу.
-частицу.
(Ответ: 0,4)
11.10.
Определить
асимметрию случайной величины,
распределенной по закону Пуассона.
(Асимметрией называется отношение
![]() ).
).
(Ответ:
![]() )
)
11.11.
В
аппаратурный отсек космической ракеты
за время ее
полета попадает
![]() элементарных частиц с вероятностью
элементарных частиц с вероятностью
![]() .
.
Условная вероятность для каждой из них попасть при этом в уязвимый блок равна р. Найти вероятность попадания в блок:
а) ровно k частиц;
б) хотя бы одной частицы.
(Ответ:
а)
![]() ;
б)
;
б)![]() )
)
11.12.
Определить
дисперсию числа атомов радиоактивного
вещества, распадающегося в единицу
времени, если даны масса вещества М,
период
полураспада
![]() ,
атомный
вес вещества А,
число
атомов в грамм-атоме
,
атомный
вес вещества А,
число
атомов в грамм-атоме
![]() .
.
Рассеиванием и поглощением частиц пренебречь.
Число
Авогадро N0
=![]() —
число атомов в грамм-атоме,
т. е. в количестве вещества, вес которого
в граммах равен атомному весу.
—
число атомов в грамм-атоме,
т. е. в количестве вещества, вес которого
в граммах равен атомному весу.
Периодом
полураспада вещества
![]() называется время, в течение которого
масса радиоактивного вещества уменьшается
в среднем вдвое.
называется время, в течение которого
масса радиоактивного вещества уменьшается
в среднем вдвое.
(Ответ:
 .
Составить дифференциальное уравнение
для среднего числа частиц в момент
времени
.
Составить дифференциальное уравнение
для среднего числа частиц в момент
времени![]() .
Приравнять среднее число частиц половине
первоначального. Полученное в результате
этого уравнение дает возможность найти
вероятность распада данной частицы;
умножая ее на число частиц, получим
.
Приравнять среднее число частиц половине
первоначального. Полученное в результате
этого уравнение дает возможность найти
вероятность распада данной частицы;
умножая ее на число частиц, получим![]() )
)
11.13.
Определить
вероятность того, что в экран площадью
![]() см2,
поставленный на расстоянии r=5
см
перпендикулярно
потоку от
см2,
поставленный на расстоянии r=5
см
перпендикулярно
потоку от
![]() -радиоактивного
вещества, попадает в течение секунды:
-радиоактивного
вещества, попадает в течение секунды:
а)
ровно десять
![]() -частиц;
-частиц;
б)
не менее
двух
![]() -частиц,
-частиц,
если
период полураспада вещества
![]() лет, масса вещества М
—
0,1 г, атомный вес вещества
А
=
238.
лет, масса вещества М
—
0,1 г, атомный вес вещества
А
=
238.
Рассеиванием и поглощением частиц пренебречь.
Число
Авогадро N0
=![]() —
число атомов в грамм-атоме,
т. е. в количестве вещества, вес которого
в граммах равен атомному весу.
—
число атомов в грамм-атоме,
т. е. в количестве вещества, вес которого
в граммах равен атомному весу.
Периодом
полураспада вещества
![]() называется время, в течение которого
масса радиоактивного вещества уменьшается
в среднем вдвое.
называется время, в течение которого
масса радиоактивного вещества уменьшается
в среднем вдвое.
(Ответ:
а)
![]() ;
б)
;
б)![]() ,
где
,
где![]() )
)
11.14. Доказать, что полиномиальное распределение
![]() ,
,
где
![]() ,
,
а
![]() ,
,
можно аппроксимировать функцией
![]() ,
,
где
![]() ,
если все вероятности
,
если все вероятности![]() ,
за исключением
,
за исключением![]() ,малы,
а
,малы,
а![]() велико.
велико.
(Указание:
Представить
![]() в виде:
в виде:
 ,
где
,
где
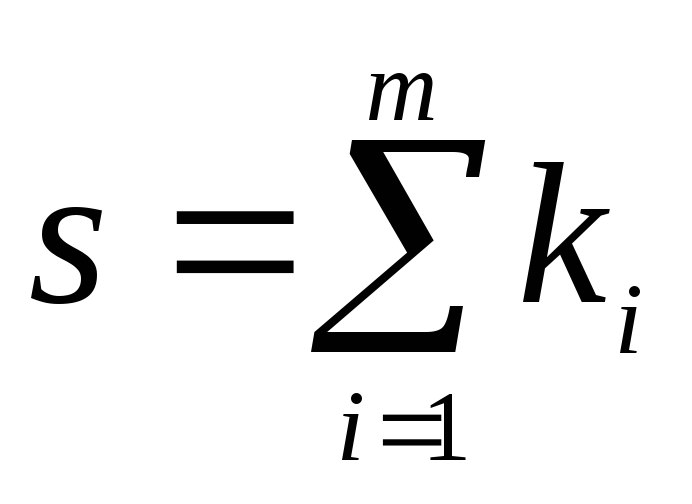 .
Так как
.
Так как![]() и
и![]() конечны, то
конечны, то )
)
