10.4. Задачи для самостоятельной работы
10.1. Плотность вероятности случайной величины Х имеет вид (закон равномерного распределения)
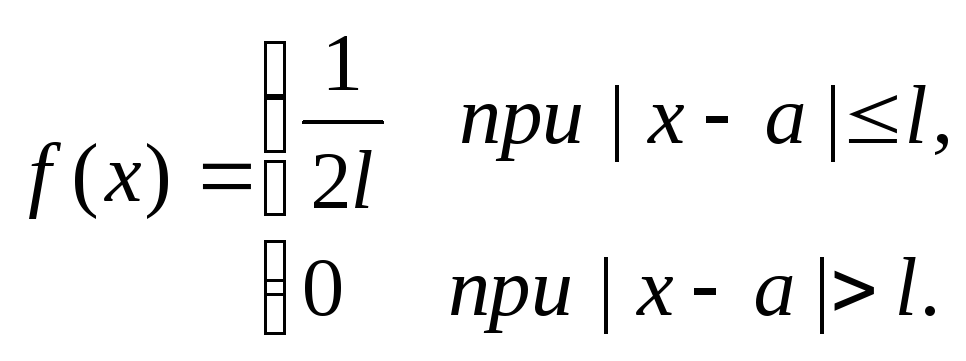
Определить:
а) 
;
б) 
;
в) найти связь между средним квадратическим и срединным отклонениями случайной величины Х.
(Ответ:
а)
;
б)
в)
)
10.2. Функция распределения случайной величины Х имеет вид (закон арксинуса)
Определить
постоянные a
и b.
Найти
и
.
(Ответ:
)
10.3. Определить математическое ожидание и дисперсию случайной величины Х, если плотность вероятности
(Ответ:
)
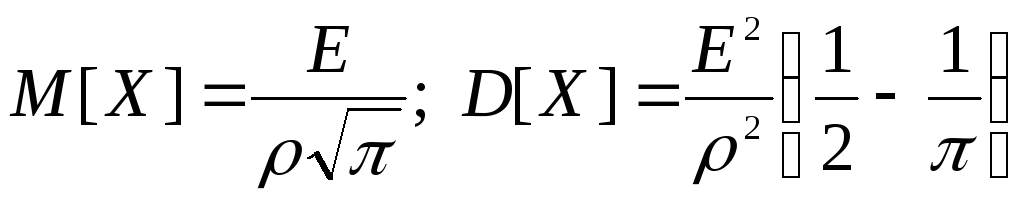10.4. Плотность вероятности случайной величины Х имеет вид (закон арксинуса)
.
Определить дисперсию и срединное отклонение.
(Ответ:
)
10.5. Плотность вероятности случайных амплитуд А боковой качки корабля определяется формулой (закон Рэлея)
,
где
-
дисперсия угла крена.
Одинаково ли часто встречаются амплитуды, меньшие и большие средней?
(Ответ:
;
)
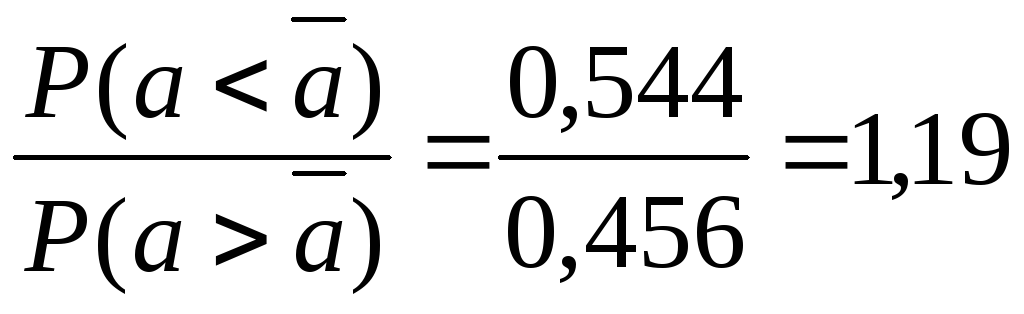10.6. Скорость молекул газа имеет плотность вероятности (закон Максвелла)
.
Найти математическое ожидание и дисперсию скорости молекул, а также величину А при заданном h.
(Ответ:
)
10.7. Плотность вероятности случайной величины X задана в виде
Определить
и
.
(Ответ:
)
10.8. Функция распределения случайной величины X имеет вид
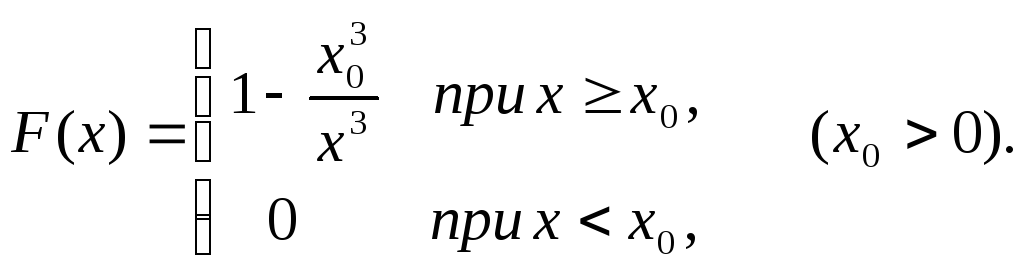
Найти М[Х] и D[X].
(Ответ:
)
10.9. Найти математическое ожидание и дисперсию случайной величины, плотность вероятности которой имеет вид (распределение Лапласа):
.
(Ответ:
)
10.10. Случайная величина X имеет плотность вероятности (гамма-распределение)
Определить параметр А, математическое ожидание и дисперсию случайной величины X.
(Ответ:
)
10.11. Случайная величина X имеет плотность вероятности (бета-распределение)
Определить параметр А, математическое ожидание и дисперсию случайной величины X.
(Ответ:
)
10.12. Случайная величина X имеет плотность вероятности
,
где
—
целое положительное число, большее 1.
Определитьпостоянную
А,
математическое
ожидание и дисперсию случайной
величины X.
(Ответ:
Указание:
Для вычисления интеграла
следует воспользоваться подстановкой
,
приводящей к бета-функции, а последнюю
выразить через гамма-функцию)
10.13.
Плотность
вероятности неотрицательной случайной
величины
X
имеет вид
(
-распределение)
,
где
.
Определить А, математическое ожидание и дисперсию случайной величины X.
(Ответ:
)
10.14. Доказать, что при выполнении условий
и
для математического ожидания случайной величины справедливо равенство
.
(Указание:
Воспользоваться соотношением
)
10.15. Вероятность обнаружения затонувшего судна за время поиска t задается формулой
.
Определить среднее время поиска, необходимое для обнаружения судна.
(Ответ:
Указание:
Обратить внимание на то, что
является функцией распределения
случайного времени поисков
,
необходимого для обнаружения судна)
10.16.
Определить
математическое ожидание m(t)
массы
радиоактивного
вещества спустя время t,
если в
начальный момент
масса вещества была
,
а вероятность распада ядралюбого
атома в единицу времени постоянна и
равна р.
(Ответ:
Указание:
Учесть, что вероятность распада любого
фиксированного атома за промежуток
времени
равна
и составить дифференциальное уравнение
дляm(t))
10.17. Определить время полураспада радиоактивного вещества, если вероятность распада ядра любого атома в единицу времени постоянна и равна р. (Время полураспада Тп определяется моментом, когда масса радиоактивного вещества в среднем уменьшается вдвое.)
(Ответ:
Указание: Воспользоваться решением задачи 10.16)
10.18. Обработка результатов одной переписи показала, что плотность вероятности возраста лиц, занимающихся научной работой, может быть представлена формулой
,
время
в годах,
.
Определить, во сколько раз число научных работников в возрасте ниже среднего превышает число научных работников в возрасте выше среднего.
(Ответ:
,
то есть научных работников, имеющих
возраст меньше среднего (среди научных
работников), больше, чем имеющих возраст
больше среднего. Средний возраст среди
научных работников
года)
10.19. Найти для распределения Стьюдента, задаваемого плотностью вероятности
,
начальные
моменты при
при
.
(Ответ:
при
,
Указание:
При
вычислении интегралов вида
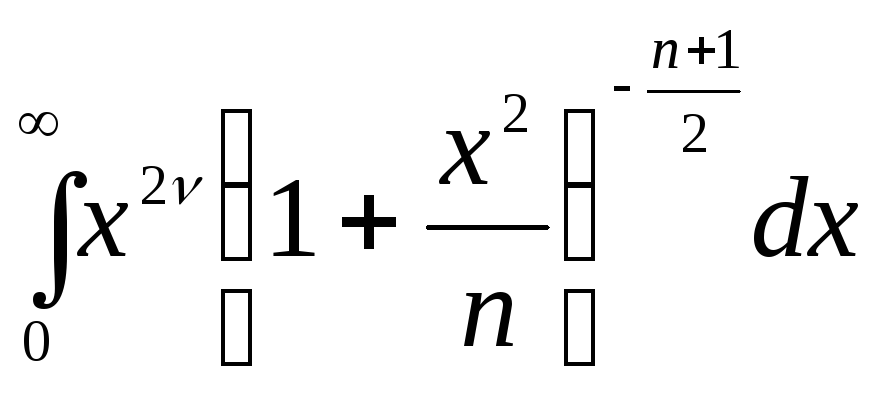произвести замену переменных
,
приводящей к бета-функции, а последнюю
выразить через гамма-функцию)
10.20. Случайная величина X подчиняется бета-распределению, т. е. имеет плотность вероятности
Найти начальный момент k-гo порядка.
(Ответ:
)
10.21.
Найти математическое ожидание и дисперсию
случайной величины, имеющей в интервале
плотность вероятности
.
(Ответ:
)
10.22.
Выразить центральный момент
через начальные моменты.
(Ответ:
,
где
)
10.23.
Выразить
начальный момент
через
центральные моменты и математическое
ожидание
.
(Ответ:
,
где
)