Занятие 5. Формула полной вероятности.

5.1. Краткая теоретическая часть

Предположим, что событие В может осуществиться с одним и только с одним из n несовместимых событий . Иными словами, положим, где событияBA_i и BA_j с разными индексами i и j несовместимы. По теореме сложения вероятностей имеем: .

Применяя теорему умножения, находим:

(5.1)

Это равенство носит название формулы полной вероятности и играет важную роль во всей дальнейшей теории.

5.2. Тест.

1. Пусть - некоторые события. Укажите 2 условия, при которых необходимо применить формулу полной вероятности для определения вероятности появления события:

а) - полная группа несовместных событий

б) - полная группа равновозможных событий

в) - полная группа независимых событий

г) - полная группа попарно несовместных и равновозможных событий

д) Событие не может произойти совместно ни с одним из событий

е) Событие может произойти совместно только с одним из событий

ж) Событие может произойти совместно с каждым из событий

2. Что означает тот факт, что - полная группа несовместных событий?

а)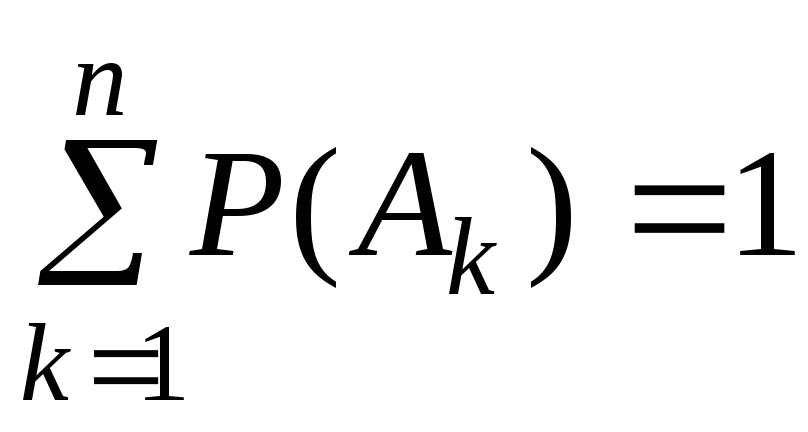

б)

в)

3. Какие из следующих групп событий ,не являются полными группами несовместных событий?

а) - извлечение шара из-той урны, содержащейбелых ичерных шаров, если шар извлекается наудачу из любой изурн

б) - извлечение шара из-той урны, содержащейбелых ичерных шаров, если шар извлекается наудачу из любых двух урн

в) - наличиебракованных лампочек среди 100 взятых наудачу из 1000, если известно, что число испорченных лампочек на 1000 штук равновозможно от 0 до 5

г) - правильный ответ студента по крайней мере наизвопросов, содержащихся в экзаменационных билетах

д) - правильный ответ студента ровно наизвопросов, содержащихся в экзаменационных билетах

4. Какой вид имеет формула полной вероятности?

а)

б)

в)

г)

5.3. Решение типовых задач

Пример 5.1. Среди n лиц разыгрываются тn выигрышей путем случайного извлечения из ящика n билетов. Одинаковы ли шансы выигрыша для любого из играющих? Когда выгоднее тащить билет?

Решение.

Обозначим через A_k событие, состоящее в извлечении выигрышного билета после k извлечений билетов из ящика. По результатам предыдущих опытов можно сделать k+1 гипотез. Пусть гипотеза H_ks означает, что из k извлеченных билетов выигрышных было s. Вероятности этих гипотез

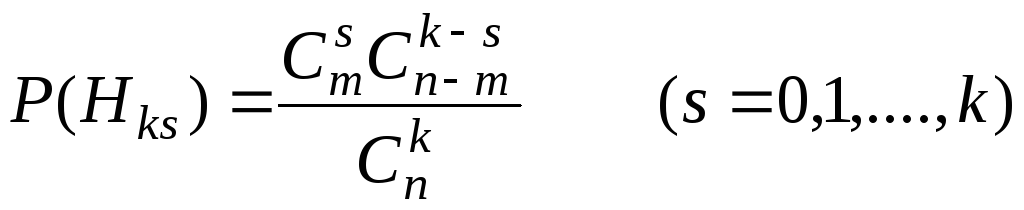
причем

_.

Так как осталось n—k билетов, из которых т—s выигрышных, то при ms

_.

По формуле полной вероятности находим

_,

где приs>m.

Данное равенство можно записать также в виде

_.

Имеем

_,

т. е. справедливо равенство

_.

Искомая вероятность Р(A_k)=при любомk. Таким образом, у всех играющих шансы одинаковы и очередность извлечения не имеет значения.

Пример 5.2. Отмеченный шар с вероятностями p и 1—p может находиться в первой или во второй урне. Вероятность извлечь отмеченный шар из урны, в которой этот шар находится, равна Р(Р 1). Как следует распорядиться правом n раз извлекать шары из любой урны, чтобы вероятность извлечения отмеченного шара хотя бы один раз была наибольшей, если шар после извлечения возвращается в урну?

Решение.

Пусть событие А — извлечение отмеченного шара.

Гипотезы: H₁—шар находится в первой урне, H₂—во второй.

По условию P(H₁)=p, Р(H₂)=1—р.

Допустим, что из первой урны извлечено т, а из второй n—т шаров. Условные вероятности извлечения отмеченного шара будут

_.

По формуле полной вероятности искомая вероятность

_.

Нужно определить т так, чтобы была наибольшей вероятность Р (А). Дифференцируя Р(A) по т (для нахождения приближенного значения т считаем m непрерывным), получаем

_.

Полагая, приходим к равенству

.

Поэтому должно быть

_.