Занятие 3. Условная вероятность. Теорема умножения вероятностей.

3.1. Краткая теоретическая часть

Условной вероятностью Р(A|В) события А называется вероятность появления этого события, вычисленная при условии, что имело место событие В.

События А и В независимы, если Р(A|В) = Р(А).

Вероятность произведения двух событий определяется по формуле

_,

которая обобщается на произведение n событий:

_.

События независимы в совокупности, если для любогоm (m =2, 3, ., n) и любых k_j (j=1, 2, ..., n), , выполняется:

_.

3.2. Тест

1. Что означает тот факт, что события А и В являются независимыми?

а) Наступление события В не изменяет вероятности наступления события А

б) Наступление события А не изменяет вероятности наступления события В

в) Появление события А исключает появление события В

г) Появление события В исключает появление события А

д) События А и В не могут наступить одновременно

е) По крайней мере одно из событий А и В обязательно наступит в ходе опыта

2. Какие из приведенных пар событий являются независимыми? Укажите 3 пары.

а) Восход солнца и пение птиц утром в ясную погоду

б) Отсутствие в аудитории лектора и отмена лекции, которую он читает

в) Отсутствие в аудитории одного студента из группы и отмена лекции, на которой он должен присутствовать

г) Сработавшая в магазине сигнализация и приезд в этот магазин сотрудников вневедомственной охраны

д) Выпадение на игральной кости определенной грани и выпадение «герба» при подбрасывании монеты

е) Показ нового фильма в кинотеатрах и выпуск очередного номера еженедельной газеты

ж) Знание студентом всех вопросов в экзаменационных билетах и успешная сдача им экзамена

з) Чрезвычайное происшествие в стране и экстренный выпуск новостей по центральному каналу телевидения

3. Какую вероятность называют условной?

а) Вероятность события А, которому благоприятствует m исходов испытания из n возможных

б) Вероятность попадания точки, брошенной в область G с квадрируемой границей, в подобласть g

в) Вероятность события А, определенную при условии, что произошло событие В, имеющее ненулевую вероятность

4. Как формулируется теорема умножения вероятностей?

а) Вероятность совместного появления двух событий равна произведению вероятности одного из них на вероятность другого

б) Вероятность совместного появления двух событий равна произведению вероятности одного из них на вероятность другого, вычисленную в предположении, что первое событие не наступит

в) Вероятность совместного появления двух событий равна произведению вероятности одного из них на вероятность другого, вычисленную в предположении, что первое событие уже наступило

г) Вероятность совместного появления двух событий равна сумме вероятностей этих событий

5. Следствие из теоремы умножения вероятностей формулируется следующим образом:

а)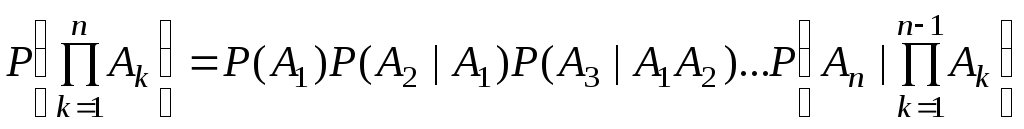

б)

в)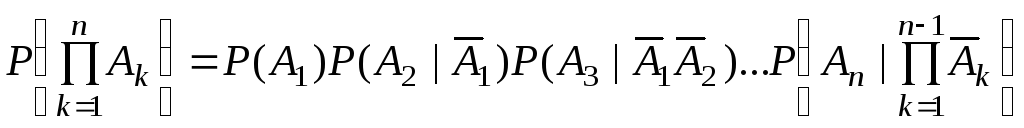

г)

6. Для каких событий применима теорема умножения вероятностей?

а) Только для независимых

б) Только для противоположных

в) Только для несовместных

г) Только в случае, когда одно из событий является невозможным

д) Только для полной группы попарно несовместных и равновозможных событий

е) Для любых событий