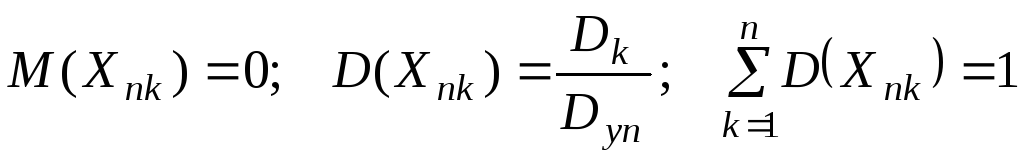- •Теория вероятностей
- •Содержание
- •Раздел 6. Законы распределения функций случайных аргументов. 90
- •1. Теоретическая часть. Введение
- •Раздел 1. Понятие события и его вероятности.
- •1.1. Предмет теории вероятности.
- •1.2. Алгебра событий. Пространство элементарных событий.
- •1.3. Классическое определение вероятности.
- •1.4. Геометрические вероятности.
- •1.5. Частота и вероятность.
- •1.6. Аксиоматическое построение теории вероятностей.
- •1.7. Условная вероятность и простейшие основные формулы.
- •1.8. Формула полной вероятности.
- •1.9 Формула Бейеса.
- •Раздел 2. Последовательные независимые испытания
- •2.1. Независимые испытания. Формулы Бернулли.
- •2.2. Обобщенная теорема о повторении опытов.
- •Раздел 3. Понятие случайной величины. Функция распределения и ее основные свойства.
- •3.1. Понятие случайной величины и функции распределения.
- •3.2. Свойства функции распределения.
- •3.3. Дискретные и непрерывные случайные величины.
- •3.4. Числовые характеристики случайных величин.
- •Раздел 4. Примеры распределений случайных величин.
- •4.1. Биномиальное распределение.
- •4.2. Теорема Пуассона
- •4.3. Закон Пуассона.
- •4.4. Равномерное распределение.
- •4.5. Показательное распределение.
- •4.6.Нормальный закон распределения.
- •Раздел 5. Системы случайных величин (случайные векторы).
- •5.1. Понятие о системе случайных величин.
- •5.2. Функция распределения системы двух случайных величин.
- •5.3. Плотность распределения системы двух случайных величин.
- •5.4. Законы распределения отдельных компонент, входящих в систему. Условные законы распределения.
- •5.5. Зависимые и независимые случайные величины.
- •5.6. Числовые характеристики системы двух случайных величин.
- •5.7. Система произвольного числа случайных величин (случайные вектора).
- •5.8. Числовые характеристики системы нескольких случайных величин.
- •Раздел 6. Законы распределения функций случайных аргументов.
- •6.1. Закон распределения функции одного случайного аргумента.
- •6.2. Закон распределения функции двух случайных величин.
- •6.3. Закон распределения суммы двух случайных величин. Композиция законов распределения.
- •6.4. Распределение произведения.
- •6.5. Распределение квадрата случайной величины.
- •6.6. Распределение частного.
- •6.7. Числовые характеристики функций случайных величин.
- •Раздел 7. Теоремы о числовых характеристиках.
- •7.1. Основные теоремы о математическом ожидании.
- •7.2. Теоремы о дисперсии случайной величины.
- •7.3. Теорема о линейной зависимости случайных величин.
- •Раздел 8. Характеристические функции.
- •8.1. Определение и простейшие свойства характеристических функций.
- •8.2. Предельные теоремы для характеристических функций.
- •Раздел 9. Предельные теоремы для случайных величин.
- •9.1. Сходимость последовательностей случайных величин.
- •9.2. Закон больших чисел.
- •9.3. Следствия закона больших чисел.
- •Раздел 10. Предельные теоремы теории вероятностей.
- •10.1. Центральная предельная теорема.
- •10.2. Теорема Ляпунова.
- •10.3. Теорема Лапласа.
- •2. Практические занятия, тесты, самостоятельная работа. Занятие 1. Непосредственный подсчет вероятности с использованием классического определения вероятности.
- •1.1. Краткая теоретическая часть.
- •1.2. Тест.
- •1.3. Решение типовых задач.
- •1.4. Задачи для самостоятельной работы.
- •Занятие 2. Геометрическое определение вероятности.
- •2.1. Краткая теоретическая часть.
- •2.2. Тест
- •2.3. Решение типовых задач
- •2.4. Задачи для самостоятельной работы
- •Занятие 3. Условная вероятность. Теорема умножения вероятностей.
- •3.1. Краткая теоретическая часть
- •3.2. Тест
- •3.3. Решение типовых задач
- •3.4. Задачи для самостоятельной работы
- •Занятие 4. Теорема сложения вероятностей.
- •4.1. Краткая теоретическая часть
- •4.2. Тест
- •4.3. Решение типовых задач
- •4.4. Задачи для самостоятельной работы
- •Занятие 5. Формула полной вероятности.
- •5.1. Краткая теоретическая часть
- •5.2. Тест.
- •5.3. Решение типовых задач
- •5.4. Задачи для самостоятельной работы
- •Занятие 6. Формула Бейеса.
- •6.1. Краткая теоретическая часть
- •6.2.Тест
- •6.3. Решение типовых задач
- •6.4. Задачи для самостоятельной работы
- •Занятие 7. Последовательные независимые испытания.
- •7.1. Краткая теоретическая часть
- •7.2. Тест
- •7.3. Решение типовых задач
- •7.4. Задачи для самостоятельной работы
- •Занятие 8. Дискретные и непрерывные случайные величины.
- •8.1. Краткая теоретическая часть а) Ряд, многоугольник и функция распределения случайной дискретной величины
- •8.2. Тест
- •А) только к дискретным случайным величинам
- •8.3. Решение типовых задач а) Ряд, многоугольник и функция распределения случайной дискретной величины
- •Б) Функция распределения и плотность вероятности непрерывной случайной величины
- •8.4. Задачи для самостоятельной работы а) Ряд, многоугольник и функция распределения случайной дискретной величины
- •Занятие 9. Числовые характеристики дискретных случайных величин.
- •9.1. Краткая теоретическая часть
- •9.2. Тест
- •9.3. Решение типовых задач
- •9.4. Задачи для самостоятельной работы
- •Занятие 10. Дискретные и непрерывные случайные величины.
- •10.1. Краткая теоретическая часть
- •10.2. Тест
- •10.3. Решение типовых задач
- •10.4. Задачи для самостоятельной работы
- •Занятие 11. Закон Пуассона.
- •11.1. Краткая теоретическая часть
- •11.2. Тест
- •11.3. Решение типовых задач
- •11.4. Задачи для самостоятельной работы
- •Занятие 12. Закон нормального распределения.
- •12.1. Краткая теоретическая часть
- •12.2. Тест
- •12.3. Решение типовых задач
- •12.4. Задачи для самостоятельной работы
- •Литература
9.3. Следствия закона больших чисел.
Пусть производиться
n
независимых опытов в каждом из которых
с вероятностью p
может произойти событие A,
пусть
![]() –
статистическая вероятность или частота
появления событияA
в серии n
– опытов.
–
статистическая вероятность или частота
появления событияA
в серии n
– опытов.
Теорема Бернулли.
При неограниченном
увеличении числа опытов
![]() частота
частота![]() сходится к вероятности
сходится к вероятности![]() по вероятности, то есть
по вероятности, то есть
![]() или
или
![]() .
.
Доказательство.
Введем в рассмотрение независимые
случайные величины
![]() - число появлений событияA
в i
– ом опыте.
- число появлений событияA
в i
– ом опыте.
![]() - дискретные случайные величины, их ряд
распределения имеет вид:
- дискретные случайные величины, их ряд
распределения имеет вид:
-
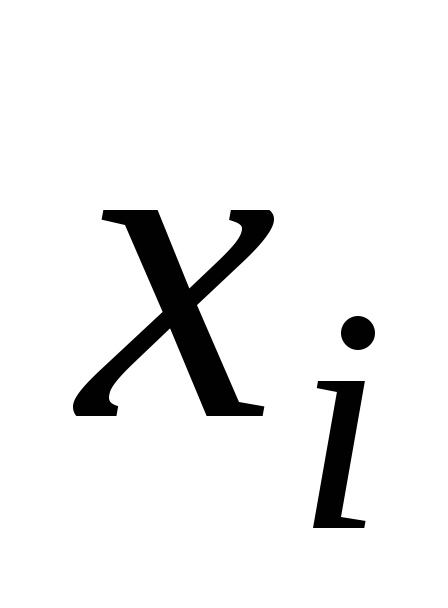
0
1
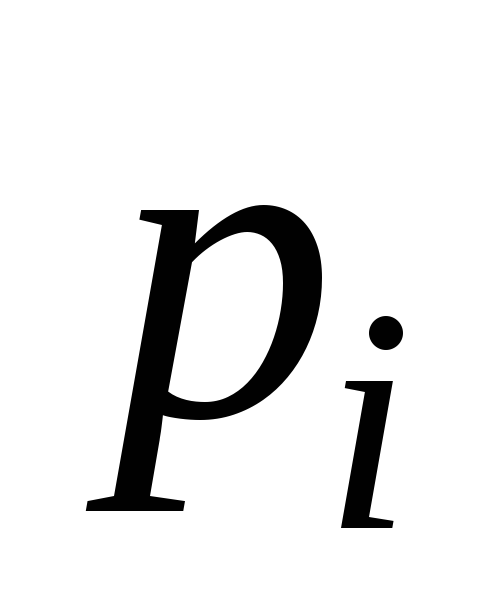
q
p
Тогда![]()
|
|
|
Так как
![]() - независимые случайные величины
- независимые случайные величины![]() ;
;![]() ,
то к ним можно применить теорему Чебышева,
учитывая, что
,
то к ним можно применить теорему Чебышева,
учитывая, что![]() ,
тогда
,
тогда или
или![]() .
.
Предельная теорема Пуассона.
Пусть производиться
n
независимых опытов. Событие A
в i
- ом опыте может произойти с вероятностью
![]() ,
тогда при
,
тогда при![]()
![]() сходиться к среднему арифметическому
вероятностей
сходиться к среднему арифметическому
вероятностей![]() по вероятности, то есть.
по вероятности, то есть.
|
|
|
Доказательство.
![]() - независимые
случайные величины(число появлений
события A
в i
– ом опыте),
имеющие следующие числовые характеристики
- независимые
случайные величины(число появлений
события A
в i
– ом опыте),
имеющие следующие числовые характеристики
![]() ,
,![]() .
Данные случайные величины удовлетворяют
условиям обобщенной теоремы Чебышева.
.
Данные случайные величины удовлетворяют
условиям обобщенной теоремы Чебышева.
Применяя её, получим
|
|
|
Раздел 10. Предельные теоремы теории вероятностей.
10.1. Центральная предельная теорема.
Центральная предельная теорема теории вероятностей представляет собой совокупность предложений, устанавливающих условия возникновения нормального закона распределения.
Пусть
на
![]() заданы
независимые случайные величины
заданы
независимые случайные величины
![]() с
числовыми характеристиками
с
числовыми характеристиками
|
|
(10.1.1) |
Рассмотрим случайные величины
|
|
(10.1.2) |
и установим условия,
при которых распределение случайной
величины
![]() с возрастаниемп
становится
сколь угодно близким к нормальному
N(0,1),
т.е.
с возрастаниемп
становится
сколь угодно близким к нормальному
N(0,1),
т.е.
![]() .
.
Будем
говорить, что последовательность
случайных величин
![]() удовлетворяет
центральной предельной теореме, если
удовлетворяет
центральной предельной теореме, если
![]() .
.
Заметим,
что
![]() означает,
что при достаточно большом n
распределение Yn
становится
близким к нормальному
означает,
что при достаточно большом n
распределение Yn
становится
близким к нормальному
![]() .
.
В самом
деле, пусть
![]() .
Тогда
для любого сколь угодно малого
.
Тогда
для любого сколь угодно малого
![]() существует
существует![]() ,
что при
,
что при![]() выполняется условие
выполняется условие
|
|
|
Здесь
![]() -
функция
распределения
-
функция
распределения
![]() :
Ф(y)
- функция
распределения
:
Ф(y)
- функция
распределения
![]() .
.
Положим
 .
Тогда
для
.
Тогда
для
![]() :
:
|
|
(10.1.3) |
Поскольку
|
|
|
где
![]() –
распределение
–
распределение
![]() ,
а
,
а
![]() -
распределение
-
распределение![]() ,
то
вместо (10.1.3)
можно записать:
,
то
вместо (10.1.3)
можно записать:
|
|
|
Случайную
величину
![]() ,
очевидно, можно представить в виде
,
очевидно, можно представить в виде
|
|
(10.1.4) |
где
 -
независимые случайные величины с
характеристиками
-
независимые случайные величины с
характеристиками
|
|
(10.1.5) |
Если
![]() - характеристическая функция
- характеристическая функция![]() ,
то
характеристическая функция
,
то
характеристическая функция
![]() случайной величины
случайной величины![]() в силу независимости
в силу независимости![]() имеет
вид:
имеет
вид:
|
|
(10.1.6) |
Теперь,
учитывая теорему единственности, вопрос
о
![]() можно свести к установлению сходимости
можно свести к установлению сходимости
|
|
(10.1.7) |
Этот
прием будет основным в доказательстве
следующей теоремы, дающей достаточное
условие для
![]() .
.
10.2. Теорема Ляпунова.
Пусть
![]() -
независимые
и одинаково распределенные случайные
величины с числовыми характеристиками
-
независимые
и одинаково распределенные случайные
величины с числовыми характеристиками
|
|
(10.2.1) |
Тогда
|
|
(10.2.2) |
Доказательство.
Прежде
всего отметим, что выражение
![]() вида (10.2.2)
совпадает с
вида (10.2.2)
совпадает с
![]() в
выражениях (10.1.2),
если считать выполненными условия
(10.2.1).
Поэтому доказательство должно сводиться
к установлению сходимости (10.1.7).
в
выражениях (10.1.2),
если считать выполненными условия
(10.2.1).
Поэтому доказательство должно сводиться
к установлению сходимости (10.1.7).
Далее,
в выражение (10.2.2)
для
![]() входят
только центрированные составляющие
входят
только центрированные составляющие
![]() ,
случайных
величин
,
случайных
величин
![]() ,
поэтому
доказательство можно проводить, полагая
в (10.2.2)
,
поэтому
доказательство можно проводить, полагая
в (10.2.2)
![]() ,
т.е. при условиях
,
т.е. при условиях
|
|
(10.2.3) |
где
![]() -
независимые
и одинаково распределенные. Поскольку
-
независимые
и одинаково распределенные. Поскольку
![]() ,
одинаково
распределены, то их характеристические
функции совпадают:
,
одинаково
распределены, то их характеристические
функции совпадают:
|
|
(10.2.4) |
Учитывая
независимость
![]() ,
получим следующее выражение
характеристической функции случайной
величины
,
получим следующее выражение
характеристической функции случайной
величины
![]() :
:
|
|
|
Отсюда следует
|
|
(10.2.5) |
Разлагая
в ряд по степеням
![]() правую часть уравнения (10.2.5)
при достаточно больших п
получим
с учетом теоремы о дифференцируемости
характеристических функций
правую часть уравнения (10.2.5)
при достаточно больших п
получим
с учетом теоремы о дифференцируемости
характеристических функций
|
|
|
Отсюда найдем
|
|
|
В силу
условия
![]() и формулы
и формулы![]() получим
получим
|
|
|
Теперь можно записать
|
|
|
Отсюда следует требуемое
|
|
|
К числу простейших форм центральной предельной теоремы относится также теорема Лапласа.