Раздел 5. Системы случайных величин (случайные векторы).

5.1. Понятие о системе случайных величин.

В практических приложениях теории вероятностей очень часто приходится сталкиваться с задачами, в которых результат опыта описы­вается двумя или более случайными величинами, образующими систему или вектор. Например, при стрельбе группой из п выстрелов совокупность точек попада­ния на плоскости может рассматриваться как система 2n случайных величин: п абсцисс и п ординат точек попадания. Условимся систему нескольких случайных величин называть случайным вектором и обозначать Х= (X₁, Х₂,...., Х_n).

Свойства системы случайных величин (или случайного вектора) не исчерпываются свойствами отдельных компонент: помимо этого, они включают также взаимные связи (зависимости) между случайными компонентами.

При рассмотрении вопросов, связанных с системами случайных величин, удобно пользоваться геометрической интерпретацией системы. Например, систему двух случайных величин (X,Y) можно изобра­жать случайной точкой на плоскости с координатами X и Y (рис. 5.1.1). Аналогично система трех случайных величин может быть изображена случайной точкой в трехмерном пространстве. Часто бы­вает удобно говорить о системе п случайных величин как о «случай­ной точке в пространстве п измерений». Вместо образа случайной точки для геометрической интерпретации системы случайных величин пользуются образом слу­чайного вектора. Систему двух случайных величин при этом рассматривают как случайный вектор на плоскости хОу, составляющие которого по осям представляют собой случайные величины X, Y (рис. 5.1.2).

При этом теория систем случайных величин рассматривается как теория случайных векторов.

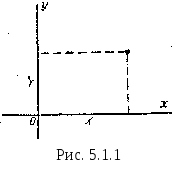
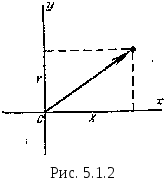
В данном курсе мы будем в зависимости от удобства изложения пользоваться как одной, так и другой интерпретацией.

Занимаясь изучением свойств случайных векторов, мы будем рассматривать как полные, исчерпывающие вероятностные характеристики — законы распределения, так и неполные — числовые характеристики.

Изложение начнем с наиболее простого случая системы двух случайных величин(двухмерного слу­чайного вектора).

5.2. Функция распределения системы двух случайных величин.

Функцией распределения системы двух случайных величин (X,Y) называется вероятность совместного выполнения двух неравенств X<х и Y<у:

(5.2.1)

Если пользоваться для геометрической интерпретации системы образом случайной точки (случайного вектора), то функция распределения F(х,у) есть не что иное, как вероятность попадания случайной точки (X,Y) в бесконечный квадрант с вершиной в точке (х,у), лежащий левее и ниже ее (рис. 5.2.1).

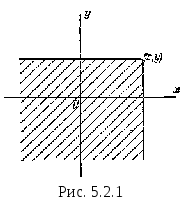
Сформулируем свойства функции распределения системы случайных величин.

1. Функция распределения F(x,у) есть неубывающая функция обоих своих аргументов, т. е.

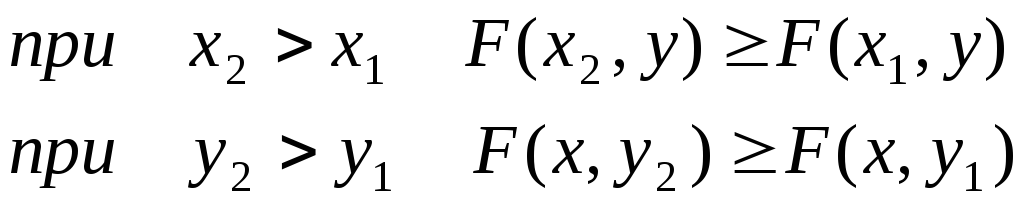
В этом свойстве функции F(х) можно наглядно убедиться, пользуясь геометрической интерпретацией функции распределения как вероятности попадания в квадрант с вершиной (х,у) (рис. 5.2.1). Действительно, увеличивая х (смещая правую границу квадранта вправо) или увеличивая у (смещая верхнюю границу вверх), мы, очевидно, не можем уменьшить вероят­ность попадания в этот квадрант.

2. Повсюду на функция распределения равна нулю:

F(x, ) = F(,y) = F(,) = 0.

В этом свойстве мы наглядно убеждаемся, неограниченно отодви­гая влево правую границу квадранта (x ) или вниз его верх­нюю границу (у) или делая это одновременно с обеими границами; при этом вероятность попадания в квадрант стремится к нулю.

3. При одном из аргументов, равном , функция распределения системы превращается в маргинальную функцию распределения случайной величины, соответствующей другому аргументу:

F (x, ) = F_l (x), F (,у) = F₂ (у),

где F₁(x), F₂(y) — соответственно маргинальные функции распределения случайных величин X и Y.

4. Если оба аргумента равны , функция распределения системы равна единице:

F(,)= 1

Действительно, при x,yквадрант с вершиной(х,у) в пределе обращается во всю плоскость хОу, попадание в которую есть достоверное событие.

Условимся событие, состоящее в попадании случайной точки (X, Y) в область D, обозначать символом (X, Y)D.

Вероятность попадания случайной точки в заданную область выражается наиболее просто в том случае, когда эта область представляет собой прямоугольник со сторонами, параллельными координатным осям.

Выразим через функцию распределения системы вероятность попадания случайной точки (X, Y) в прямоугольник R, ограниченный абсциссами иординатамии(рис. 5.2.2).

Тогда событие (X,Y)R будет равносильно произведению двух событий: Хи Х. Выразим вероятность этого события через

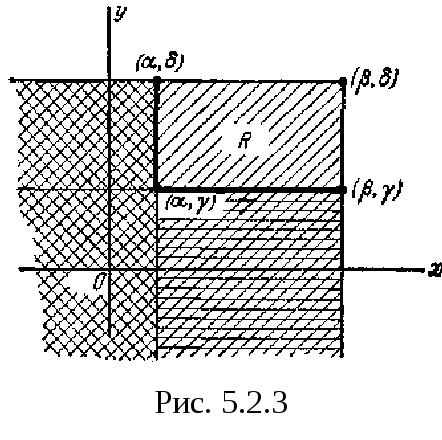
функцию распределения системы. Для этого рассмотрим на плоскости хОу четыре бесконечных квадранта с вершинами в точках рис. 5.2.3.

Очевидно, вероятность попадания в прямоугольник R равна вероятности попадания в квадрант минус вероятность попадания в квадрантминус вероятность попадания в квадрантплюс вероятность попадания в квадрант(так как мы дважды вычли вероятность попадания в этот квадрант). Отсюда получаем формулу, выражающую вероятность попадания в прямоугольник через функцию распределения системы:

(5.2.2)