3.2. Свойства функции распределения.

Свойство 1. Функция распределения любой случайной величины, есть неубывающая функция.

Зная функцию распределения случайной величины X, можно определить вероятность неравенства x₁X<x₂ при любых . В самом деле, если через A обозначить событие, состоящее в том, что X, примет значение, меньшее чем x₂, через В—событие, состоя­щее в том, что X < x₁, наконец, через С — событие x₁X<x₂ ,то, очевидно, имеет место следующее равенство:

(3.2.1)

Так как события В и С несовместимы, то Р(А)=P(B)+Р(C).

Но

(3.2.2)

поэтому

(3.2.3)

Так как, по определению, вероятность есть неотрицательное число, то из равенства (3.2.3) следует, что при любых x₁ и (x₂>x₁) имеет место неравенство

(3.2.4)

что и требовалось доказать.

Свойство 2. .Так как, функция распределения , то согласно свойств вероятности при любом х удовлетворяет неравенству

(3.2.5)

Свойство 3. Функция распределения может иметь не более чем счетное множество скачков.

Мы скажем, что функция распределения F(х) имеет при х=x₀ скачок, если

(3.2.6)

В самом деле, скачков размера , функция распределения может иметь не более одного, скачков размера от одной четвертой до половины - не более трех. Вообще скачков размера отдоможет быть не более чем. Совершенно ясно, что мы можем пронумеровать все скачки, расположив их по величине, начиная с больших значений и повторяя равные значения столько раз, сколько скачков этой величины имеет функцияF(х).

Свойство 4. . Определим иравенствами

и докажем, что .

Действительно, так как неравенство X< + достоверно, то

Обозначим через событие, состоящее в том, что . Так как событие , эквивалентно сумме событий , то на основании расширенной аксиомы сложения . Следовательно, при

Отсюда, принимая во внимание неравенства (3.2.5), заключаем, что при .

Свойство 5. Функция распределения непрерывна слева.

Выберем какую-нибудь возрастающую последовательность , сходящуюся к x.

Обозначим через A_n, событие . Тогда ясно, что , при i>j, и произведение всех событий A_n, есть невозможное событие. По аксиоме непрерывности должно быть

что и требовалось доказать.

3.3. Дискретные и непрерывные случайные величины.

Определение 1. Случайная величина X называется дискретной, если множество значений, которое она может принимать не более чем счетно, то есть либо конечно либо счетно. (Множество называется счетным, если каждому элементу можно поставить в соответствие число натурального ряда).

Пусть X – дискретная случайная величина принимает значение при этом будем предполагать, что всепопарно различны.

Определение 2. Рядом распределения дискретной случайной величины X называется совокупность пар чисел , где- возможные значения случайной величины, аp_i – вероятности, с которыми она принимает эти значения. События образуют полную группу попарно не совместных событий. Ряд распределения можно представить в виде таблицы(Табл.3.3.1) или многоугольника распределения(Рис.3.3.1).

Табл.3.3.1

xi	X1	x2	…	xn
pi	P1	p2	…	pn

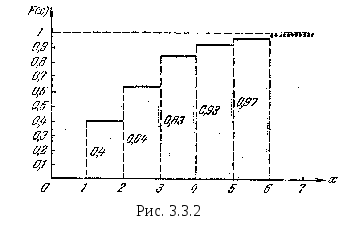
Зная ряд распределения, либо многоугольник распределения можно построить функцию распределения случайной величины(Рис. 3.3.2), которая является исчерпывающей характеристикой случайной величины X.

(3.3.6.)

Отметим, что величина скачка в точке, являющейся возможным значением случайной величины, равна вероятности p_i того, что случайная величина Х примет значение x_i.

Пример. Производится три выстрела по мишени. Вероятность попадания при одном выстреле равна 0,4. Построить ряд распределения для числа попаданий в мишень(см. Табл.3.3.2).

Х - число попаданий в мишень при трех выстрелах.

Табл.3.3.2

xi	0	1	2	3
pi	0,216	0,432	0,288	0,064

В качестве другого важного класса случайных величин можно выделить непрерывные случайные величины.

Определение 3. Распределение случайной величины X называется непрерывным, если существует такая, интегрируемая функция , что выполняется условие

(3.3.7)

Функция f(x) называется плотностью вероятности(плотностью распределения вероятности) или дифференциальным законом распределения.

Свойства плотности распределения.

1)- не отрицательная функция.

2)Если F(x) – дифференцируемая функция, то

3)Вероятность того, что случайная величина будет находится в пределах определяется соотношением

(3.3.8)

4)

(3.3.9)

Плотность распределения, так же как и функция распределения есть одна из форм закона распределения. Однако она не является универсальной характеристикой случайной величины, так как существует только для непрерывных случайных величин.

Рассмотрим непрерывную случайную величину Х с плотностью распределения f(x)( Рис.3.3.3).

Выделим элементарный участок dx. Вероятность попадания величины Х на этот участок f(x)dx называют элементом вероятности.