Критерии качества измерений

Качество измерений характеризуется точностью, достоверностью, правильностью, сходимостью и воспроизводимостью измерений, а также размером допустимых погрешностей.

Точность - это качество измерений, отражающее близость их результатов к истинному значению измеряемой величины. Высокая точность измерений соответствует малым погрешностям как систематическим, так и случайным.

Точность количественно оценивают обратной величиной модуля относительной погрешности. Например, если погрешность измерений равна 10^-6, то точность равна 10⁶.

Достоверностьизмерений характеризует степень доверия к резуль-татам измерений. Достоверность оценки погрешностей определяют на основе законов теории вероятностей и математической статистики. Это даёт возможность для каждого конкретного случая выбирать средства и методы измерений, обеспечивающие получение результата, погрешности которого не превышают заданных границ с необходимой достоверностью.

Под правильностьюизмерений понимают качество измерений, отражающее близость к нулю систематических погрешностей в результатах измерений.

Сходимость- это качество измерений, отражающее близость друг к другу результатов измерений, выполняемых в одинаковых условиях. Схо-димость измерений отражает влияние случайных погрешностей.

Воспроизводимость- это такое качество измерений, которое отра-жает близость друг к другу результатов измерений, выполняемых в различ-ных условиях (в различное время, в различных местах, различными мето-дами и средствами).

Планирование измерений

В простейшем случае планирование измерений сводится к нахождению оптимального числа измерений nнабора величин X₁,...X_n, а затем статистических характеристик:

среднего арифметического ,

где - среднее арифметическое выборки;- его доверительный интервал;

среднего квадратического выборкиS_n_n(n).

Доверительный интервал, на величину которого истинное значение может отличаться от выборочного,

,

где t_n-1- табличный коэффициент Стьюдента, зависящий от доверительной вероятностиРи числа измерений (n-1). На практике выбирают:Р 0,68, что соответствует1;Р 0,95 соответствует2;Р0,997 соответствует3.

Наибольшее число требуемых испытаний

,

где m- число предварительных экспериментов, заведомо меньшее, чем требуемое.

Таким образом, исходными, предварительно выбранными величинами при планировании измерений, являются: X - максимальное допустимое отклонение среднего арифметического;Р- доверительная вероятность;m- число предварительных испытаний.

Законы распределения случайных величин

В метрологии при измерениях все наблюдаемые величины являются случайными и могут иметь самые различные законы распределения. Однако наиболее распространенными при обработке результатов наблюдений являются нормальный закон Гаусса и закон распределения Стьюдента, при разработке цифровых систем приборов используется квантование сигналов, в котором применяется треугольный и равномерный законы распределения, при измерении природных явлений, применяя теорию массового обслуживания, используется биномиальное распределение и т.п. Мы опишем только наиболее распространенные, отсылая к специальной литературе по теории вероятности и математической статистике (ГОСТ Р 50779.10-2000 (ИСО 3534.1-93)).

Нормальное распределение Гаусса. Закон нормальное распределение Гаусса занимает особое положение в теории вероятности, математической статистике и теории обработки результатов измерений. Он широко применяется в физике. Этому закону распределения подчиняются многие природные явления и процессы. Он является также предельным – к нему стремятся многие другие законы распределения при возрастании числа измерений.

Плотность распределения случайной величины при нормальном распределении Гаусса выражается в виде:

где - математическое ожидание ();

- стандартное отклонение (СКО);

- дисперсия ().

Скос и эксцесс равны нулю:

.

Интеграл вероятности имеет вид:

Стандартное нормальное распределение. Если заменить переменные (т.е. их пронормировать и заменить)-стандартизованная случайная величина, то получимстандартное нормальное распределениес плотностью распределения в виде

а интеграл вероятности Гауссапреобразуется, и будет иметь вид

Функция табулирована [41], если таблица приведена для интеграла

,

(её иногда называют функцией Лапласа), то в этом случае

.

Примечание.При пользовании таблицами для избегания ошибок вычислений следует обращать внимание на то, для какой функции они составлены (на интеграл).

Для стандартного нормального распределения

.

Стандартное нормальное распределение обозначают символом N(0, 1) и называют: нормированное нормальное распределение,стандартное распределение Лапласа-Гаусса (ГОСТ Р 50779.10-2000 ).

Связь с интегралом ошибок. Интегралом ошибок называют функцию

Интеграл ошибок у нас в стране распространения не получил, но за рубежом имеет применение.

Интеграл вероятности Гаусса связан с интегралом ошибок следующим соотношением:

В литературе нормальный закон называют по-разному:

- нормальный закон Гаусса,

- Гауссовское распределение,

- второй закон Лапласа,

- Лаплассовское распределение,

- нормированная функция Лапласа,

- распределение Гаусса-Лапласа,

- распределение Лапласа-Гаусса (ГОСТ Р 50779.10-2000 ).

Нормальный закон распределения для погрешностей. Плотность нормального закона распределения для погрешностей имеет вид:

,

где .

Свойства кривой распределения для случайных величин

1. Кривая распределения симметрична.

2. Точки перегиба кривой распределения находятся на оси абсцисс .

3. Вероятность того, что погрешности не выйдут за пределы , составляет.

4. Вероятность того, что погрешности не выйдут за пределы , составляет.

5. Вероятность того, что погрешности не выйдут за пределы , составляет.

6. Вероятность того, что погрешности не выйдут за пределы , составляет.

7. Вероятность того, что погрешности не выйдут за пределы , составляет.

8. При нормальном законе распределения погрешность в среднем может встретиться 1 раз на каждые 3 измерения.

9. При нормальном законе распределения погрешность в среднем может встретиться 1 раз на каждые 22 измерения.

10. При нормальном законе распределения погрешность в среднем может встретиться 1 раз на каждые 370 измерений.

11. При нормальном законе распределения погрешность в среднем может встретиться 1 раз на каждые 157870 измерений.

12. При нормальном законе распределения погрешность в среднем может встретиться 1 раз на каждые 1743983 измерений.

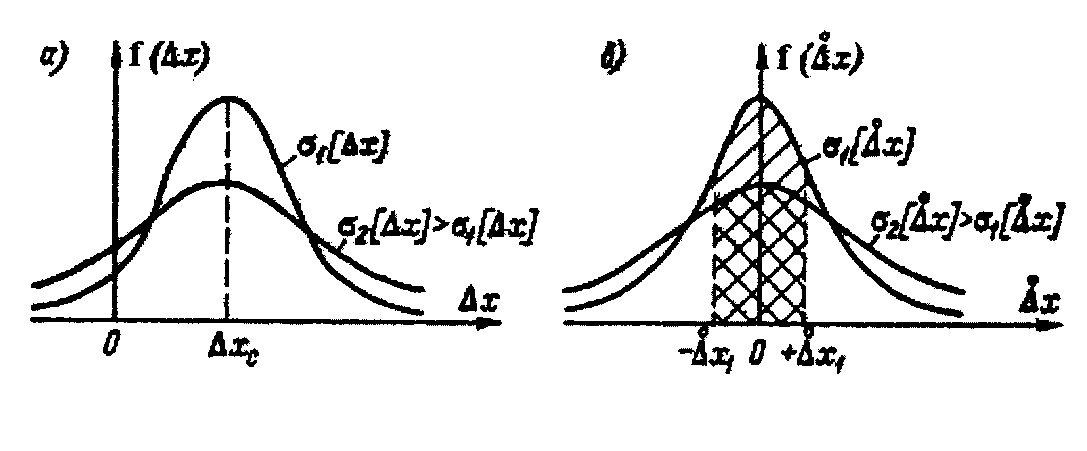
Рис. 1.2. Нормальный закон распределения погрешности измерений (а) и случайной составляющей погрешности измерений (б).

В практической деятельности часто используют свойства нормального закона (рис. 1.2). Так, например, при нормальном законе распределения случайных погрешностей со среднеквадратическим отклонением часто пользуются доверительным интервалом от —3до +3, для которого доверительная вероятность равна 0,9973. Такая доверительная вероятность означает, что при наблюдениях в среднем из 370 случайных погрешностей только одна погрешность по абсолютному значению будет больше 3. Так как на практике число отдельных измерений редко превышает несколько десятков, появление даже одной случайной погрешности, большей, чем 3, маловероятное событие, наличие же двух подобных погрешностей почти невозможно. Это позволяет с достаточным основанием утверждать, что все возможные случайные погрешности измерения, распределенные по нормальному закону, практически не превышают по абсолютному значению 3(правило «трех сигм»). Отсюда же исходит и«правило шести сигм»(интервал от -3до +3равен 6) , применяемое в Всеобщем управлении качеством (TQM).

Интервалы шире чем 3, как правило, применяют очень редко, так как это считается излишним, однако, например, в технике грузовые устройства (краны, гаки) рассчитываются с четырехкратным запасом прочности.

Распределение Стьюдента, (t-распределение).Распределение вероятностей непрерывной случайной величины, с плотностью распределения вероятностей

,

где с параметром;

Г – гамма – функция.

Распределение Стьюдента с возрастанием числа степеней свободы стремится к нормальному закону. Функция табулирована.

Данный закон распределения широко используется при обработке результатов многократных измерений.

Равномерный закон распределения.Если погрешность измерений с одинаковой вероятностью может принимать любые значения, не выходящие за некоторые границы, то такая погрешность описывается равномерным законом распределения. При этом плотность вероятности погрешностипостоянна внутри этих границ и равна нулю вне этих границ. Равномерный закон распределения представлен на рис. 1.3. Аналитически он может быть записан так:

при ;

при ;

Рис. 1.3. Равномерный закон распределения

Трапециевидный закон распределения.Это распределение графически изображено на рис. 1.4,а.Погрешность имеет такой закон распределения, если она образуется из двух независимых составляющих, каждая из которых имеет равномерный закон распределения, но ширина интервала равномерных законов различна. Например, при последовательном соединении двух измерительных преобразователей, один из которых имеет погрешность, равномерно распределенную в интервале, а другой — равномерно распределенную в интервале, суммарная погрешность преобразования будет описываться трапециевидным законом распределения.

Треугольный закон распределения (закон Симпсона). Это распределение (см. рис. 1.4,б) является частным случаем трапециевидного, когда составляющие имеют одинаковые равномерные законы распределения.

Рис. 1.4. Трапециевидный (а) и треугольный (б) законы распределения